
Языковые эксперементы
7 постов

7 постов
2 поста

3 поста

23 поста
![Хайку код[т]](http://s15.pikabu.ru/images/series/2024/09/10/1725922956197399959.png)
7 постов
Предыдущая статья: Включения действий при разборе и итог пройденных тем в vk.com
Статья для повторения: От перепутья к перепутью, часть вторая: Разбор языка арифметики
В привычной нами записи выражения, знак операции (далее оператор) записываются между значениями (далее операндами):
а + б
Такая форма называется инфиксной (калька - вкрепной).
Так же используется префиксная (докрепная) запись, когда операторы пишутся до операндов:
+ а б
и постфиксная (закрепная) запись, когда операторы пишутся за операндами:
а б +
Ниже показаны ещё примеры:
Префиксная и постфиксная запись также именуются прямая и обратная польская нотация (далее ОПН), в честь её изобретателя польского логика Яна Лукасевича. Отличительная их черта, то что в них не используются скобки для обособления вычисления.
Используем рекурсивный спуск по рассмотренной нами грамматике, где в качестве чисел целые без знака:
Грамматика с унарным минусом и плюсом:
Г: В -> ДС
С -> ε | +ДС | -ДС
Д -> РП | -Д | +Д
П -> ε | *РП | /РП
Р -> ч | (В)
Звенья цепочки ОПН опишем набором трёх типов:
1. Операнд - целые числа.
2. Одноместный оператор - однооп, это унарный минус и плюс.
3. Двуместный оператор - двуоп, это минус, плюс, умножить, делить.
Ниже представлено полное описание звена ОПН:
Соберём звенья в список, который будет представлять нашу ОПН. Для этого отметим 3 действия на отделах рисунка порядка:
Д1 - Создать хрон. Переменная хранящая звено до момента добавления в список.
Д2 - Запомнить. Помещаем встреченное звено в хрон.
Д3 - Добавить. Записываем в список ОПН.
Ниже показаны отделы и процедуры со встроенными действиями в разбор:
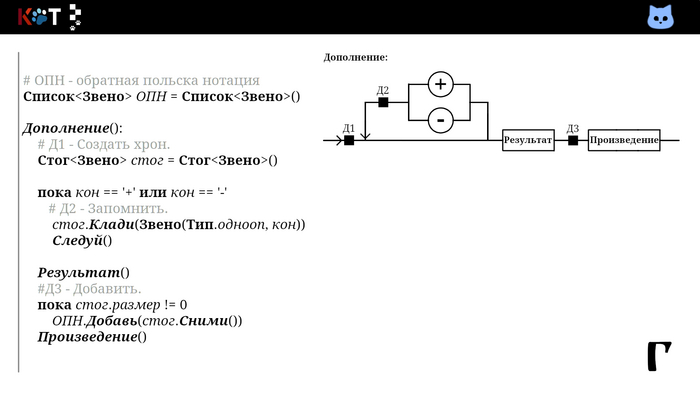
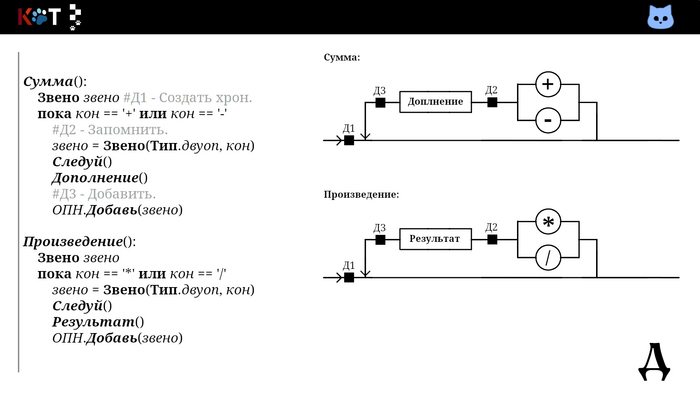
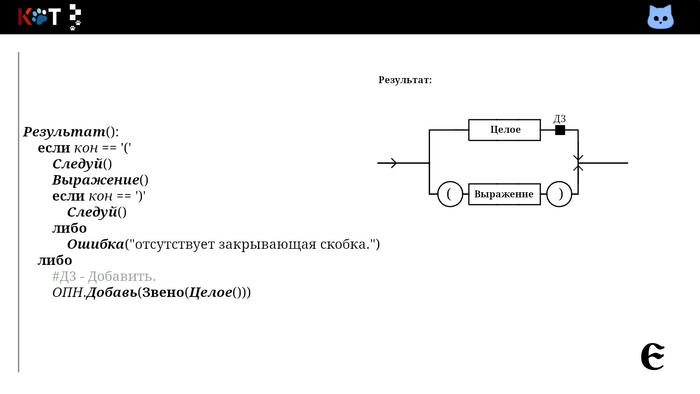
Так мы добавляем в первую очередь операнды, затем операторы в порядке их приоритетов. Всмотритесь в процедуру «Дополнениее». В качестве хрона используется стог (англ. stack), так как запоминаются несколько знаков сразу, их следует вспомнить в обратном порядке.
Осмыслим следующее: рекурсивный разборщик выступает теперь не только в качестве распознавателя, но и переводчика. Ведь мы получили цепочку принадлежащую другому формальному языку, который можно описать так:
Грамматика обратной польской нотации:
Г:В -> ч | П`П
П`-> чПО
П -> ВОП | ε
где:
В - ВЫРАЖЕНИЕ
О - ОПЕРАТОР
П - ПРАВОЕ_ПОДВЫРАЖЕНИЕ
П`- ПОДВЫРАЖЕНИЕ
ч - ЧИСЛО
Остановитесь на минутку, осмыслите.
Ниже изображена схема устройства вычисления ОПН - Стог-машина (Stack machine), а на следующем её описание. Для примера использована ОПН:
1 2 3 * + 4 -
Которая получена из инфиксной записи:
1 + 2 * 3 - 4


Стог-машина состоит из:
Стога - в котором хранятся промежуточные значения.
Набора двухместных и одноместных операций.
Движка - который читает ОПН, управляет стогом и обращается к набору операций.
ОПН обладает свойством: действия применяются последовательно при её чтении, на чём и основана работа стог-машины:
Если звено операнд, то кладём число в стог.
Если звено однооп, снимаем верхнее число обрабатываем, итог кладём в стог.
Если звено двуоп, снимаем два верхних числа и применяем операцию. Причём первое значение операции - второе верхнее, а второе - первое верхнее. Итог кладём в стог.
По окончанию чтения ОПН, итог вычисления оказывается на дне стога, одним.
Не стоит думать, что рассмотренный способ единственный для получения ОПН. Есть так же алгоритм Дейкстры перевода выражения в ОПН, но я не знаю стоит ли его разобрать или сразу перейти к обсуждению включения действий в «Провидца», ранее нами рассматриваемого.
Поэтому решение будет зависить от вас:
Ну на это всё, быть добру, хорошего настроения. Подписывайся. =)
Точно! Для любознательных и внимательных читателей, ещё одна не позиционная система счисления.
Предыдущая статья: От перепутья к перепутью, часть третья, итоговая: Требования к предопределённому распознанию языка в vk.com
Здравствуйте! Для составления табеля возьмём немного упрощённую рассмотренную нами грамматику арифметических выражений:
Г: В → ДС
С → +ДС | ε
Д → РП
П → *РП | ε
Р → ч | (В)
Вот её рисунок порядка, который поможет нам прояснить некоторые моменты:
Теперь придём к соглашению используемых определений:
1. Правило вывода тождественно понятию продукция.
2. Пусть есть некоторая продукция П → α, тогда левая часть называется именем продукции, то есть П, а правая часть цепью, то есть α.
3. Цепь состоит из звеньев, коими являются конечные и неконечные символы.
Сперва нам следует научиться собирать множества Перед и След, также известные как множества First и Follow.
Перед - это множество конечных символов, которые могут встретиться первыми при разложении неконечного символа, также может включать в себя пустую цепочку (ε).
След - это множество конечных символов, которые могут встретиться после разложения неконечного символа, также множество для стартового обязательно включает в себя символ ограничитель.
Символ ⊂ - означает «входит». Символ ∈ - означает «содержит». Символ ∉ - означает «не содержит». Символ \ - означает «исключает».
Имея продукцию П → α, Перед(П) вычисляется:
Если α - конечный символ , то Перед(П) ∈ α, Перед(α) = {α}.
Если цепь α это ε (пустая цепочка), то добавим ε к Перед(П).
Пусть α состоит из последовательности символов П → Н₁Н₂ … Нₘ :
а) К Перед(П) идут в придачу все множества Перед(Н₁₊ₖ) \ ε, где k >= 0, пока Перед(Н₁₊ₖ) ∈ ε и 1 + k < m, завершая придачей Перед(Н₁₊ₖ) ∉ ε или Перед(Нₘ) (см. п 3.б).
б) Если Н₁₊ₖ последний, то есть 1 + k = m, тогда Перед(Нₘ) ⊂ Перед(П) включая ε, если Перед(Нₘ) ∈ ε.
Звучит устрашающе, но на самом деле всё проще чем кажется, для этого воспользуемся рисунком порядка. Будем как бы разворачивать некоторые его отделы, зелёным цветом отметим конечные символы входящие в множества. Последний рисунок построен по другой грамматике, который лучше отображает суть п3.
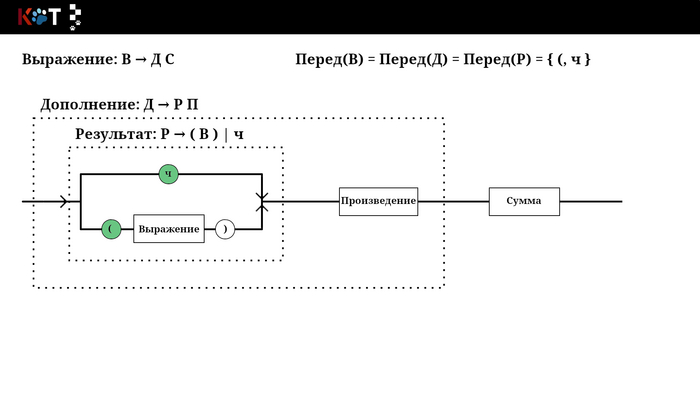
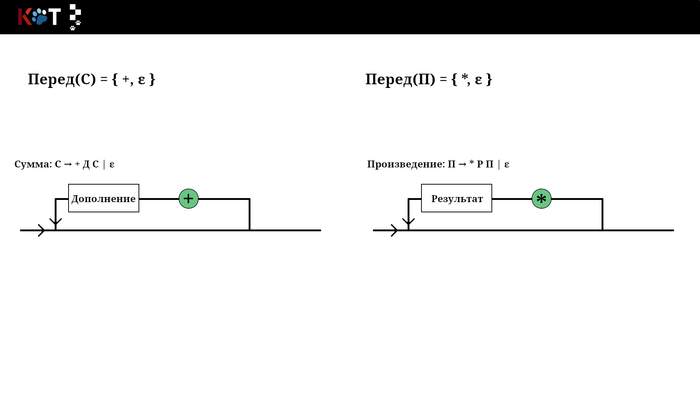
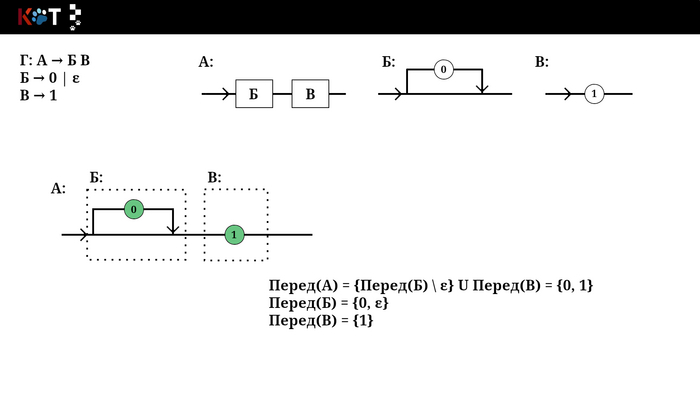
Отображение переда, листай → …
Раз уже мы решили отобразить множества на рисунке, давайте посмотрим теперь на множество След, а потом опишем как его получить. Красным отмечены символы которые попадают в множества.
α и β - произвольные цепочки.
Поместим # в След(П), если П - стартовый символ, # - правый ограничитель потока.
Если есть продукция А → αПβ, то все элементы множества Перед(β) кроме ε попадают в множество След(П).
Если есть продукция А → αП или А → αПβ, где Перед(β) содержит ε, то След(А) входит в След(П).
Большая часть пути пройдена, осталось научится создавать табель. Что он из себя представляет? А он представляет из себя пары конечного и неконечного символа и связанные с этими парами продукции. И так, для каждой продукции П → α выполним:
Для каждого конечного k из Перед(α) добавим П → α в ячейку Т[П,k].
Если Перед(α) ∈ ε, то для каждого k из След(П) добавляем П → α
в Т[П,k]. Если Перед(α) ∈ ε и След(П) ∈ #, то добавляем П → α и в Т[П,#].
Например, есть продукция В → ДС: Перед(ДС) = Перед(Д) = { (, ч }, тогда добавим эту продукция в Т[В, (] и в Т[В, ч]. В конечном итоге мы получим следующий табель:
Сей табель используется в движке распознавания, который мы рассмотрим в следующей части. Также, табель можно построить для любой грамматики, что позволяет нам определить обладает ли грамматика ЛЛ(1)-свойствами, то есть если у нас оказывает более одной продукции на одну пару, значит что данная грамматика не приндлежит к классу ЛЛ(1)-грамматикам.
Подписывайтесь! =) Псевдокоды прикрепляю и повторите: Автомат с магазинной памятью (стог-памятью) и КС-языки



Псевдокот
Просматривал сериал "Во все тяжкие" и залип на вступительные титры. Вспомнил, что обозначения хим. элементов на русском применяются в металлургии, оказывается, что там только-лишь металлы, как бы и логично. В итоге решил попробовать написать сокращения сам, да так, чтобы не было разночтений с латиницей. Создано исключительно из любопытства, как художественное произведение. Вдруг кто-то хотел увидеть.
Не знаю каким боком оказалась у меня в детстве на полке его книга "Гражданин галактики", но эта книжка сильно на меня повлияла. Спустя большее время, когда появились интернеты, скачал книгу вроде бы как "Число зверя" и было очень забавно читать, про немыслимые объёмы памяти в 1 терабайт. Очень-очень забавно читать это из будущего.
Пикабу подсветил, что комментарий большой и его следует вывести в отдельный пост, что уж так и быть освежу память об этом фантасте.
У них по этой книге есть видео лекции, держите ссылки:
https://www.youtube.com/playlist?list=PLaFqU3KCWw6JgufXBiW4dEB2-tDpmOXPH - для тупоконечников.
https://rutube.ru/plst/439869/ - для остроконечников.
Или наоборот, вы там сами как-то определитесь. Пост без рейтинга.