Разбор КС-языка по табелю, часть первая: Создание табеля
Предыдущая статья: От перепутья к перепутью, часть третья, итоговая: Требования к предопределённому распознанию языка в vk.com
Здравствуйте! Для составления табеля возьмём немного упрощённую рассмотренную нами грамматику арифметических выражений:
Г: В → ДС
С → +ДС | ε
Д → РП
П → *РП | ε
Р → ч | (В)
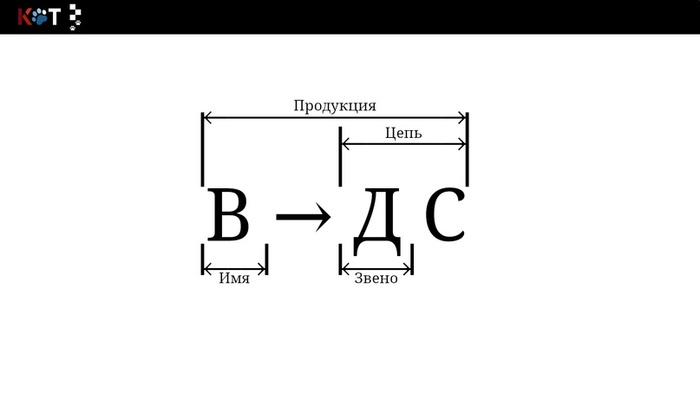
Вот её рисунок порядка, который поможет нам прояснить некоторые моменты:
Теперь придём к соглашению используемых определений:
1. Правило вывода тождественно понятию продукция.
2. Пусть есть некоторая продукция П → α, тогда левая часть называется именем продукции, то есть П, а правая часть цепью, то есть α.
3. Цепь состоит из звеньев, коими являются конечные и неконечные символы.
Сперва нам следует научиться собирать множества Перед и След, также известные как множества First и Follow.
Что такое множество «Перед»?
Перед - это множество конечных символов, которые могут встретиться первыми при разложении неконечного символа, также может включать в себя пустую цепочку (ε).
Что такое множество «След»?
След - это множество конечных символов, которые могут встретиться после разложения неконечного символа, также множество для стартового обязательно включает в себя символ ограничитель.
Как получить Перед(П)?
Символ ⊂ - означает «входит». Символ ∈ - означает «содержит». Символ ∉ - означает «не содержит». Символ \ - означает «исключает».
Имея продукцию П → α, Перед(П) вычисляется:
Если α - конечный символ , то Перед(П) ∈ α, Перед(α) = {α}.
Если цепь α это ε (пустая цепочка), то добавим ε к Перед(П).
Пусть α состоит из последовательности символов П → Н₁Н₂ … Нₘ :
а) К Перед(П) идут в придачу все множества Перед(Н₁₊ₖ) \ ε, где k >= 0, пока Перед(Н₁₊ₖ) ∈ ε и 1 + k < m, завершая придачей Перед(Н₁₊ₖ) ∉ ε или Перед(Нₘ) (см. п 3.б).
б) Если Н₁₊ₖ последний, то есть 1 + k = m, тогда Перед(Нₘ) ⊂ Перед(П) включая ε, если Перед(Нₘ) ∈ ε.
Звучит устрашающе, но на самом деле всё проще чем кажется, для этого воспользуемся рисунком порядка. Будем как бы разворачивать некоторые его отделы, зелёным цветом отметим конечные символы входящие в множества. Последний рисунок построен по другой грамматике, который лучше отображает суть п3.
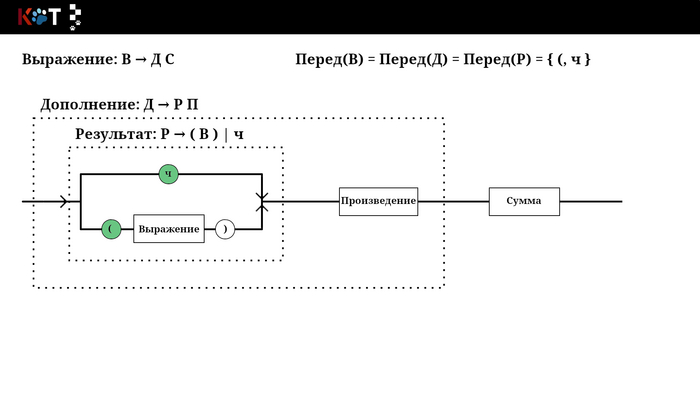
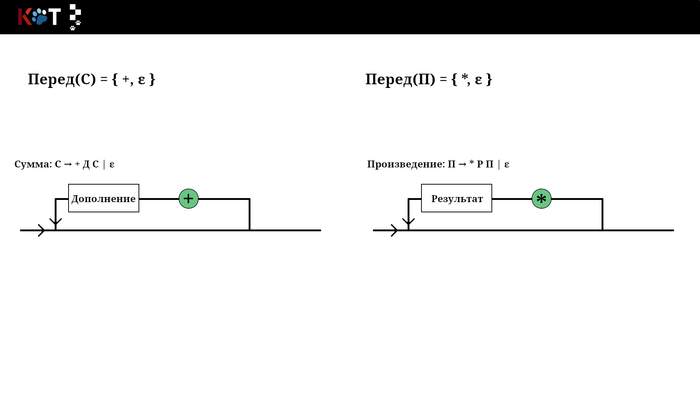
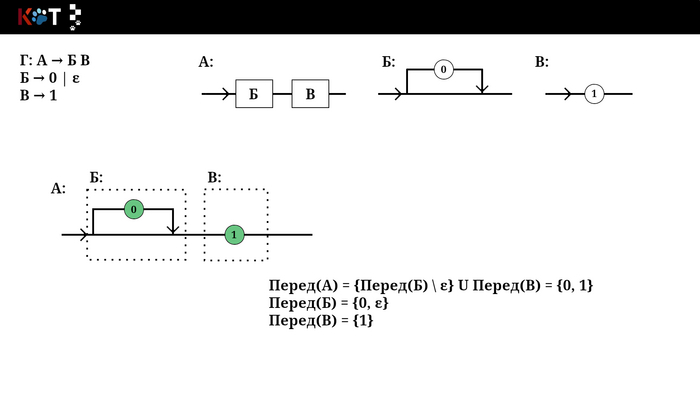
Отображение переда, листай → …
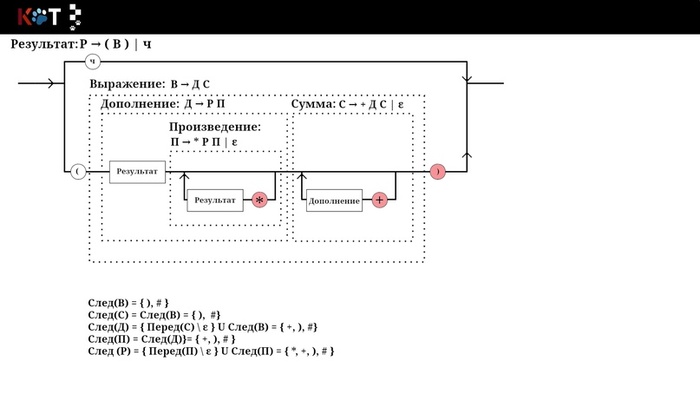
Раз уже мы решили отобразить множества на рисунке, давайте посмотрим теперь на множество След, а потом опишем как его получить. Красным отмечены символы которые попадают в множества.
Как получить След(П)?
α и β - произвольные цепочки.
Поместим # в След(П), если П - стартовый символ, # - правый ограничитель потока.
Если есть продукция А → αПβ, то все элементы множества Перед(β) кроме ε попадают в множество След(П).
Если есть продукция А → αП или А → αПβ, где Перед(β) содержит ε, то След(А) входит в След(П).
Строим табель.
Большая часть пути пройдена, осталось научится создавать табель. Что он из себя представляет? А он представляет из себя пары конечного и неконечного символа и связанные с этими парами продукции. И так, для каждой продукции П → α выполним:
Для каждого конечного k из Перед(α) добавим П → α в ячейку Т[П,k].
Если Перед(α) ∈ ε, то для каждого k из След(П) добавляем П → α
в Т[П,k]. Если Перед(α) ∈ ε и След(П) ∈ #, то добавляем П → α и в Т[П,#].
Например, есть продукция В → ДС: Перед(ДС) = Перед(Д) = { (, ч }, тогда добавим эту продукция в Т[В, (] и в Т[В, ч]. В конечном итоге мы получим следующий табель:
Сей табель используется в движке распознавания, который мы рассмотрим в следующей части. Также, табель можно построить для любой грамматики, что позволяет нам определить обладает ли грамматика ЛЛ(1)-свойствами, то есть если у нас оказывает более одной продукции на одну пару, значит что данная грамматика не приндлежит к классу ЛЛ(1)-грамматикам.
Подписывайтесь! =) Псевдокоды прикрепляю и повторите: Автомат с магазинной памятью (стог-памятью) и КС-языки



Псевдокот



Лига образования
6K поста22.5K подписчика
Правила сообщества
Публиковать могут пользователи с любым рейтингом. Однако мы хотим, чтобы соблюдались следующие условия:
ДЛЯ АВТОРОВ:
Приветствуются:
-уважение к читателю и открытость
-желание учиться
Не рекомендуются:
-публикация недостоверной информации
ДЛЯ ЧИТАТЕЛЕЙ:
Приветствуются:
-конструктивные дискуссии на тему постов
Не рекомендуются:
-личные оскорбления и провокации
-неподкрепленные фактами утверждения
В этом сообществе мы все союзники - мы все хотим учиться! :)