
Языковые эксперементы
7 постов

7 постов
2 поста

3 поста

23 поста
![Хайку код[т]](http://s15.pikabu.ru/images/series/2024/09/10/1725922956197399959.png)
7 постов
Предыдущая статья: Включения действий при разборе и итог пройденных тем в vk.com
Статья для повторения: От перепутья к перепутью, часть вторая: Разбор языка арифметики
В привычной нами записи выражения, знак операции (далее оператор) записываются между значениями (далее операндами):
а + б
Такая форма называется инфиксной (калька - вкрепной).
Так же используется префиксная (докрепная) запись, когда операторы пишутся до операндов:
+ а б
и постфиксная (закрепная) запись, когда операторы пишутся за операндами:
а б +
Ниже показаны ещё примеры:
Префиксная и постфиксная запись также именуются прямая и обратная польская нотация (далее ОПН), в честь её изобретателя польского логика Яна Лукасевича. Отличительная их черта, то что в них не используются скобки для обособления вычисления.
Используем рекурсивный спуск по рассмотренной нами грамматике, где в качестве чисел целые без знака:
Грамматика с унарным минусом и плюсом:
Г: В -> ДС
С -> ε | +ДС | -ДС
Д -> РП | -Д | +Д
П -> ε | *РП | /РП
Р -> ч | (В)
Звенья цепочки ОПН опишем набором трёх типов:
1. Операнд - целые числа.
2. Одноместный оператор - однооп, это унарный минус и плюс.
3. Двуместный оператор - двуоп, это минус, плюс, умножить, делить.
Ниже представлено полное описание звена ОПН:
Соберём звенья в список, который будет представлять нашу ОПН. Для этого отметим 3 действия на отделах рисунка порядка:
Д1 - Создать хрон. Переменная хранящая звено до момента добавления в список.
Д2 - Запомнить. Помещаем встреченное звено в хрон.
Д3 - Добавить. Записываем в список ОПН.
Ниже показаны отделы и процедуры со встроенными действиями в разбор:
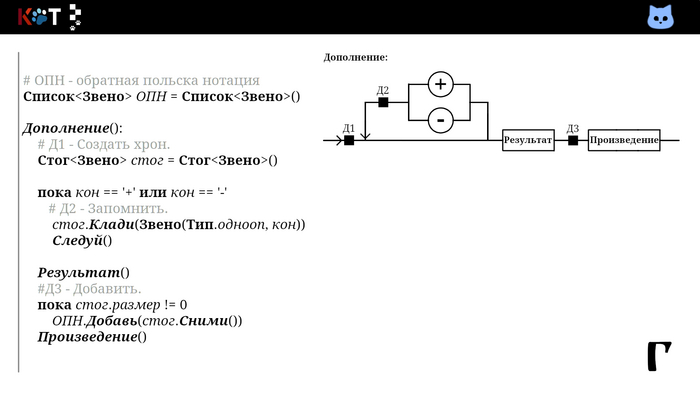
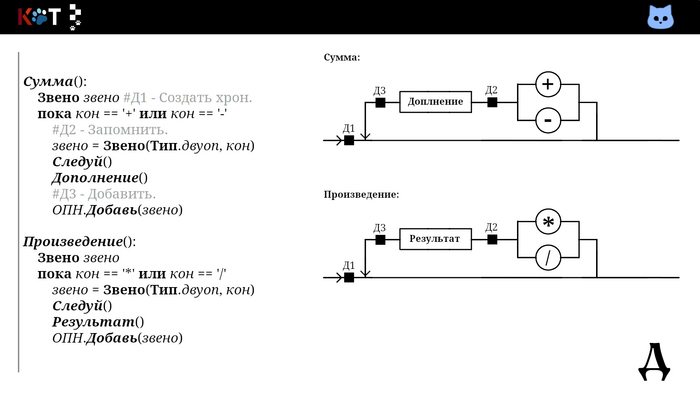
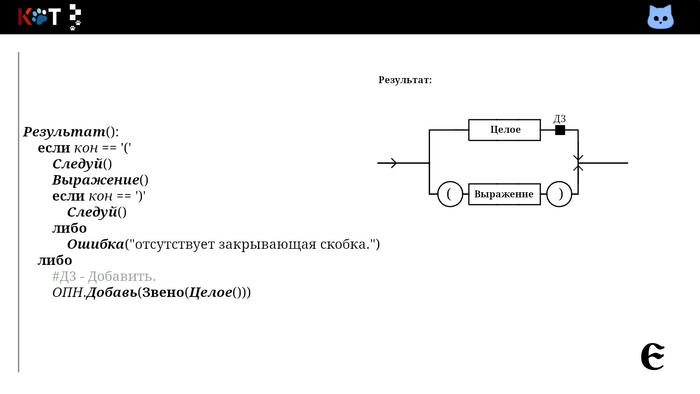
Так мы добавляем в первую очередь операнды, затем операторы в порядке их приоритетов. Всмотритесь в процедуру «Дополнениее». В качестве хрона используется стог (англ. stack), так как запоминаются несколько знаков сразу, их следует вспомнить в обратном порядке.
Осмыслим следующее: рекурсивный разборщик выступает теперь не только в качестве распознавателя, но и переводчика. Ведь мы получили цепочку принадлежащую другому формальному языку, который можно описать так:
Грамматика обратной польской нотации:
Г:В -> ч | П`П
П`-> чПО
П -> ВОП | ε
где:
В - ВЫРАЖЕНИЕ
О - ОПЕРАТОР
П - ПРАВОЕ_ПОДВЫРАЖЕНИЕ
П`- ПОДВЫРАЖЕНИЕ
ч - ЧИСЛО
Остановитесь на минутку, осмыслите.
Ниже изображена схема устройства вычисления ОПН - Стог-машина (Stack machine), а на следующем её описание. Для примера использована ОПН:
1 2 3 * + 4 -
Которая получена из инфиксной записи:
1 + 2 * 3 - 4


Стог-машина состоит из:
Стога - в котором хранятся промежуточные значения.
Набора двухместных и одноместных операций.
Движка - который читает ОПН, управляет стогом и обращается к набору операций.
ОПН обладает свойством: действия применяются последовательно при её чтении, на чём и основана работа стог-машины:
Если звено операнд, то кладём число в стог.
Если звено однооп, снимаем верхнее число обрабатываем, итог кладём в стог.
Если звено двуоп, снимаем два верхних числа и применяем операцию. Причём первое значение операции - второе верхнее, а второе - первое верхнее. Итог кладём в стог.
По окончанию чтения ОПН, итог вычисления оказывается на дне стога, одним.
Не стоит думать, что рассмотренный способ единственный для получения ОПН. Есть так же алгоритм Дейкстры перевода выражения в ОПН, но я не знаю стоит ли его разобрать или сразу перейти к обсуждению включения действий в «Провидца», ранее нами рассматриваемого.
Поэтому решение будет зависить от вас:
Ну на это всё, быть добру, хорошего настроения. Подписывайся. =)
Точно! Для любознательных и внимательных читателей, ещё одна не позиционная система счисления.
Предыдущая статья: Регулярки - применение. Итог темы об автоматных языках в vk.com
Статья для повторения:Эквивалентность и однозначность грамматики или почему иногда 2+2*2=8?
При разборе автоматных языков мы ведь не строили никаких деревьев? Нет ли здесь противоречия? Нет. Из-за свойства автоматной грамматики её правила вида A → a и A → ε всегда приводят к конечным символам, а правило вида A → aB всегда задаёт однозначную последовательность для ДКА, и все деревья автоматных грамматик приобретают вид:
Поэтому нам будет полезно ввести определение однозначности не прибегая к дереву. Для этого рассмотрим две грамматики мат.выражений:
G1: E → E + E | E – E | E * E | E / E | x | ( E )
G2:
E → T | E + T | E – T
T → M|T * M| T / M
M → x | (E)
Попробуем построить выражение x + x * x более чем одним левосторонним выводом, для G1:
E => E * E => E + E * E => x + E * E => x + x * E => x + x * x
E => E + E => x + E => x + E * E => x + x * E => x + x * x
Теперь для G2:
E =>E + T=>T + T =>M + T=>x + T=>x + T * M=>x + M * M =>x + x * M => x + x * x
А вот второй вывод для G2 мы не можем построить, так как по правилам грамматики, мы не можем подставить * или операнд (x) раньше, чем + . Если мы построим деревья, то мы увидим, что в G1 они будут выглядеть по разному, ну а в G2 у нас всегда только одно дерево. Таким образом:
КС-грамматика называется однозначной, если для каждого предложения языка, порождаемого этой грамматикой, существует единственный левосторонний вывод или единственный правосторонний вывод.
Теперь о главном признаке: Если для некоторого неконечного символа А в грамматике, при выводе цепочки мы заново приходим к разложению А, а слева и справа от символа у нас уже имеются непустые цепочки конечных и неконечных символов, говорят, что такая грамматика имеет самовложение. К примеру наша грамматика G2, такой и является:
E => T => M => ( E )
Самовложение характерный признак КС-грамматики в противном случае:
КС-грамматика, не содержащая самовложения, эквивалентна автоматной грамматике.
Итак, на этом урок окночен.
З.Ы. Если вы в своей задаче встречаетесь с самвложением, отложите Regex, выпейте чаю, освободите себя от дурных мыслей, Regex-ы вам не нужны. Подписывайтесь.
По просьбе #comment_317948560
Предыдущая статья: Регулярные выражения и регулярные множества - ещё один способ задания автоматного языка в vk.com
Чем выгодно отличаются регулярные выражения от рисунка порядка и записи грамматики, так это то, что они представляют из себя строки. Что даёт нам возможность легко обрабатывать их программно и автоматизированно создавать распознаватели автоматных языков. Реализация которых может быть представлена в виде таких схем:
В предыдущей статье, показана таблица соответствий регулярных выражение с участками рисунка порядка, а в предпредстатье создание распознавателя не прибегая к таблицам переходов.
Регулярные выражения (далее РВ) по своей сути являются языком из алфавита { |, (, ), *, a}, где а - множество различных символов алфавита задаваемого языка. Можно ли с помощью РВ задать язык РВ? Ответ: нет, так как язык РВ не является автоматным, из-за самовложения он является КС-языком. Ниже представлена его грамматика с учётом приоритетов операций:
R → T | R ′′|′′ T
T → M | RM
M → a | M* | ( R ) | ε
Запись ′′|′′ представляет знак | используемый в регулярных выражениях.
При реализации РВ, человеческая лень с одной стороны упростила запись РВ , с другой усложнило понимание и чтение их, но это спорное утверждение. Была расширена нотация языка с помощью сокращений, для кол-ва повторений:
a? = (a|)
a+ = (aa*)
a{2,4} = (aa|aaa|aaaa)
Сокращение для «или»:
[abcd] = (a|b|c|d) - нужно отметить ещё, что символы между [ и ] не нужно экранировать.
Сокращения часто встречающихся множеств, один пример:
\d = (0|1|2|3|4|5|6|7|8|9)
А то и вовсе добавлены управляющие символы движка распознавателя, для указания где в строке нужно искать совпадение в ^ начале или в $ конце? В любом случае вам придётся открывать руководство конкретно-используемого инструмента, так как на долго в голове всё это удержать не возможно.
С помощью всего этого запись: (+|-|)(0|1|2|3|4|5|6|7|8|9)(0|1|2|3|4|5|6|7|8|9)* превратилась в [+-]?\d+ , но вам никто не запрещает писать по «старинке».
В этой же статье я хотел вам показать взаимосвязь регулярных выражений с автоматными языками и распознавателями.
Итог: С помощью автоматных грамматик и регулярных выражений определяется синтаксис простейших конструкций языков программирования, таких как идентификаторы, различные литералы цифр, знаки операций.
Путеводитель по пройденным статьям:
1. Что такое язык программирования? Не спешим отвечать, знакомимся с определением формальных языков
2. Грамматика языка и порождающие грамматики. Сказ о «правильных» скобочках
3. Хомски и его иерархия грамматик
4. Дерево вывода предложения (сентенции) грамматики. Синтаксическое дерево
5. Задача разбора, для чего она нужна? Или что такое parsing?
6. Эквивалентность и однозначность грамматики или почему иногда 2+2*2=8?
7. Графы автоматных грамматик. Что же, начинаем знакомится с конечными автоматами?
8. Конечные автоматы, что там внутри?
9. Обещанная реализация КА и попытка создать таблицу переходов не детерминированному автомату
10. Преобразование НКА в ДКА, один из алгоритмов
11. Синтаксические диаграммы автоматных языков - рисунок порядка автоматных языков
12. Регулярные выражения и регулярные множества - ещё один способ задания автоматного языка
Ну как-то так, друзья. Дальше в лес КС-грамматик, присоединяйтесь.
Регулярные выражения и регулярные множества - ещё один способ задания автоматного языка.
Предыдущая статья: Синтаксические диаграммы автоматных языков - рисунок порядка автоматных языков. в vk.com
Ещё одним способом задать язык является регулярное выражение. Регулярным выражением обозначают множество цепочек, которое называют регулярное множество. Чтобы задать регулярное выражение для некого алфавита Σ следуют учитывать 6 правил:
Отдельный символ из алфавита Σ есть регулярное выражение. Например символ а ∈ Σ (символ из алфавита Σ) задаёт множество {а}.
Пустая цепочка ε есть регулярное выражение, задаёт множество {ε}
Если R и Q - регулярные выражения, то запись RQ тоже регулярное выражение, которое обозначает сцеплённое множество, где первая цепочка пары образуется выражением R, а вторая выражением Q. Сцепление ещё называют конкатенацией.
Если R и Q - регулярные выражения, то запись R | Q тоже регулярное выражение, которое обозначает объединение множеств цепочек заданных выражениями R и Q. | - знак читается как «или».
Если R регулярное выражение, то запись R* тоже регулярное выражение, которое обозначает множество, которое получается путём повторения цепочек множества заданное R. Повторение ещё называют итерация.
Если R регулярное выражение, то запись (R) тоже регулярное выражение и обозначает тоже самое множество, что и R.
Предполагаем приоритет операции, высший имеет «*» - повторение, затем сцепление и низший «|» («или»). Скобки используются для изменения порядка операций.
Зачастую при записи регулярного выражения запись ε опускают и вводится дополнительный оператор «один раз и более» обозначенный символом «⁺», что значит R⁺=RR*. Вот так это выглядит на примере языка целых чисел со знаком:
(+ | – | ) (0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 )⁺
Теорема Клини гласит: Автоматные языки являются регулярными множествами. Регулярные множества являются автоматными языками.
Из вышесказанного значит, что мы любую автоматную грамматику можем записать в виде регулярного выражения и наоборот.
И чтобы вам было проще понять правила сделаем таблицу соответствия правил с участками рисунка порядка (синтаксической диаграммы) языка.
На этом урок окончен. В следующем мы обсудим регулярные выражения на практике и подытожим тему автоматных языков. Новоиспечённые подписываемся, с нами интересно. Дайте пятюню.
Если символ - это выделение смысла, то знак - его отображение.
Два разных знака могут символизировать одно и то же. К примеру, кириллическая буква А и Ⰰ из глаголицы символизируют одно и то же, непосредственно и сам звук этой буквы. Саму идею этого "А" . Звук тоже является знаком, но форма его отображения иная.
Но так же один и тот же знак может трактоваться по разному, к примеру, возьмём запись "лук". Запись "лук" является знаком.
Когда мы пишем: "Порежь лук для супа". Мы понимаем, что речь идёт об овоще.
Но когда пишем: "Он взял лук, натянул тетиву и стрельнул" . Мы понимаем, что речь идёт об оружии.
Таким образом, знак является подвижным и меняет смыслы от окружения, в то время когда символ фиксирует мысль.
Аршумент - это не аргумент, но человек ором и шумом пытается подать информацию под его предлогом.