Mathos

Префиксная и постфиксная запись также именуются прямая и обратная польская нотация (далее ОПН), в честь её изобретателя польского логика Яна Лукасевича. Отличительная их черта, то что в них не используются скобки для обособления вычисления.

Получение ОПН из инфиксной записи

Используем рекурсивный спуск по рассмотренной нами грамматике, где в качестве чисел целые без знака:

Грамматика с унарным минусом и плюсом:
Г: В -> ДС
С -> ε | +ДС | -ДС
Д -> РП | -Д | +Д
П -> ε | *РП | /РП
Р -> ч | (В)

Звенья цепочки ОПН опишем набором трёх типов:
1. Операнд - целые числа.
2. Одноместный оператор - однооп, это унарный минус и плюс.
3. Двуместный оператор - двуоп, это минус, плюс, умножить, делить.

Ниже представлено полное описание звена ОПН:

Соберём звенья в список, который будет представлять нашу ОПН. Для этого отметим 3 действия на отделах рисунка порядка:
Д1 - Создать хрон. Переменная хранящая звено до момента добавления в список.
Д2 - Запомнить. Помещаем встреченное звено в хрон.
Д3 - Добавить. Записываем в список ОПН.

Ниже показаны отделы и процедуры со встроенными действиями в разбор:

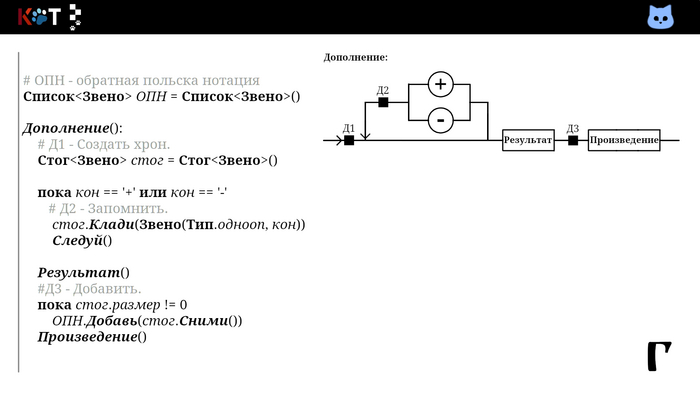
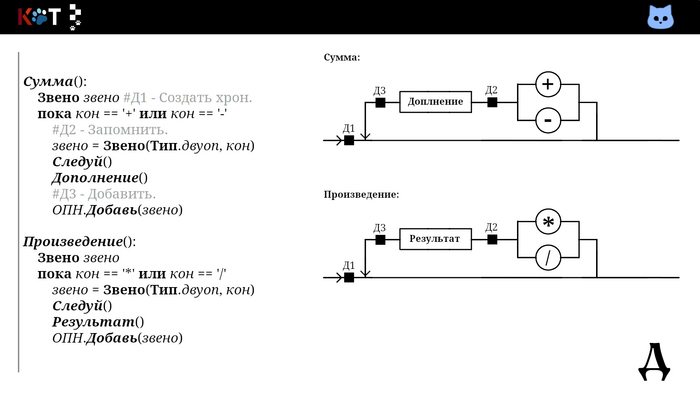
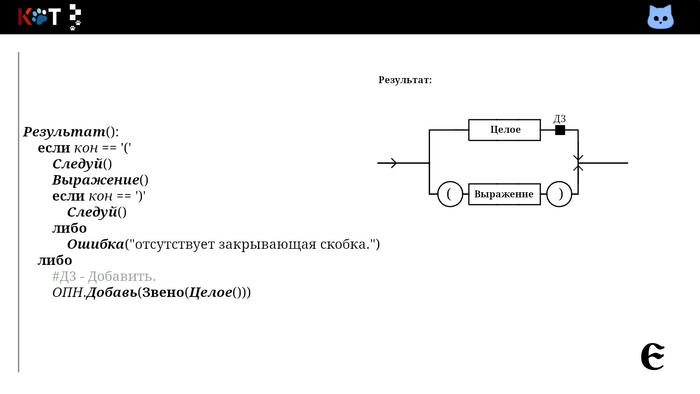
Так мы добавляем в первую очередь операнды, затем операторы в порядке их приоритетов. Всмотритесь в процедуру «Дополнениее». В качестве хрона используется стог (англ. stack), так как запоминаются несколько знаков сразу, их следует вспомнить в обратном порядке.

Осмыслим следующее: рекурсивный разборщик выступает теперь не только в качестве распознавателя, но и переводчика. Ведь мы получили цепочку принадлежащую другому формальному языку, который можно описать так:

Грамматика обратной польской нотации:
Г:В -> ч | П`П
П`-> чПО
П -> ВОП | ε

где:

В - ВЫРАЖЕНИЕ
О - ОПЕРАТОР
П - ПРАВОЕ_ПОДВЫРАЖЕНИЕ
П`- ПОДВЫРАЖЕНИЕ
ч - ЧИСЛО

Остановитесь на минутку, осмыслите.

Вычисление ОПН

Ниже изображена схема устройства вычисления ОПН - Стог-машина (Stack machine), а на следующем её описание. Для примера использована ОПН:

1 2 3 * + 4 -

Которая получена из инфиксной записи:

1 + 2 * 3 - 4

Стог-машина состоит из:

1. Стога - в котором хранятся промежуточные значения.

2. Набора двухместных и одноместных операций.

3. Движка - который читает ОПН, управляет стогом и обращается к набору операций.

ОПН обладает свойством: действия применяются последовательно при её чтении, на чём и основана работа стог-машины:

1. Если звено операнд, то кладём число в стог.

2. Если звено однооп, снимаем верхнее число обрабатываем, итог кладём в стог.

3. Если звено двуоп, снимаем два верхних числа и применяем операцию. Причём первое значение операции - второе верхнее, а второе - первое верхнее. Итог кладём в стог.

4. По окончанию чтения ОПН, итог вычисления оказывается на дне стога, одним.

В заключении

Не стоит думать, что рассмотренный способ единственный для получения ОПН. Есть так же алгоритм Дейкстры перевода выражения в ОПН, но я не знаю стоит ли его разобрать или сразу перейти к обсуждению включения действий в «Провидца», ранее нами рассматриваемого.

Поэтому решение будет зависить от вас:

Ну на это всё, быть добру, хорошего настроения. Подписывайся. =)
Точно! Для любознательных и внимательных читателей, ещё одна не позиционная система счисления.

Автоматные грамматики. Все правила такой грамматики имеют одну из трех форм: A → aB, A → a, A → ε , напомню что ε - это пустая цепочка.

Если вы достаточно внимательны, то можете заметить, что автоматные грамматики частный случай КС-грамматик, КС-грамматики частный случай КЗ-грамматик, КЗ-грамматики частный случай произвольных и когда говорят к примеру о КС-грамматике, говорят о грамматике не являющиеся автоматной. Фух…

Сейчас вам могут показаться эти определения абсолютно бесполезными, но они нам помогут понять конечный автомат, и в основном я буду писать о КС-грамматиках и автоматных, так как в основном они имеют практический интерес. Но перед обсуждением КА нам понадобится разобрать 2 темы, дерево вывода и задачи разбора (да, да парсинг), для чего они нужны что они такое.

З. Ы. Какому типу грамматик относится G = ( {(, )}, {S}, {S → (S), S →SS, S → ε}, S)?
Всем здоровья и улыбайтесь по чаще.

S - начальный нетерминал, с чего начинаются все выводы цепочек языка.

Уже появились мысли, как записать язык «правильных» скобочек?

Не мучайтесь, вот ответ: G = ( {(, )}, {S}, {S → (S), S →SS, S → ε}, S)

Пример вывода:

S => (S) => (SS) => ((S)(S)) => (()())

Результат вывода называют сентенцией (от sentence — предложение), то что может предложить наша грамматика.

Итого, таким образом с помощью нашей Gрамматики, мы можем вывести некое множество цепочек (предложений, сентенций) над алфавитом Т, которое составляет наш язык L(T).

А вот о типах грамматик, о тех что Хомски рассказывает, мы поговорим чуть позже. Чтожъ, мои милые братцы и сестрицы, а на том пока.

Цепочки обозначим греческими буквами. Примеры цепочек над алфавитом Σ₂:

α = аббва

β = аб

γ = ба

δ = в

Пустая цепочка — цепочка, не содержащая символов, ни одного символа. Обозначаем буквой ε.

Теперь воспользуемся нашей буквой Σ, но уже для обозначения множества цепочек.

Σ = {α, αγ, β, δ, δ⁴, ε}

Запись αγ обозначает склеивание (конкатенацию), добавление символов цепочки γ к символам цепочки α справа.

Степень в записи δ⁴ означает кол-во повторений символов цепочки δ, т. е δ⁴ = вввв.

Теперь мы можем дать определение формальному языку:

Формальным языком над алфавитом Σ называется произвольное множество цепочек, составленных из символов Σ.

Затем делаем запрос в поисковой системе находим определение языка программирования:

Язы́к программи́рования — формальный язык, предназначенный для записи компьютерных программ. Язык программирования определяет набор лексических, синтаксических и семантических правил, определяющих внешний вид программы и действия, которые выполнит исполнитель (обычно — ЭВМ) под её управлением.

Ну хоть с первым предложением разобрались. А дальше я пока всё, буду узнавать что такое порождающая грамматика Хомски (Чомски, Chomsky).