
Языковые эксперементы
7 постов

7 постов
2 поста

3 поста

23 поста
![Хайку код[т]](http://s15.pikabu.ru/images/series/2024/09/10/1725922956197399959.png)
7 постов
Предыдущая статья: Включения действий при разборе и итог пройденных тем в vk.com
Статья для повторения: От перепутья к перепутью, часть вторая: Разбор языка арифметики
В привычной нами записи выражения, знак операции (далее оператор) записываются между значениями (далее операндами):
а + б
Такая форма называется инфиксной (калька - вкрепной).
Так же используется префиксная (докрепная) запись, когда операторы пишутся до операндов:
+ а б
и постфиксная (закрепная) запись, когда операторы пишутся за операндами:
а б +
Ниже показаны ещё примеры:
Префиксная и постфиксная запись также именуются прямая и обратная польская нотация (далее ОПН), в честь её изобретателя польского логика Яна Лукасевича. Отличительная их черта, то что в них не используются скобки для обособления вычисления.
Используем рекурсивный спуск по рассмотренной нами грамматике, где в качестве чисел целые без знака:
Грамматика с унарным минусом и плюсом:
Г: В -> ДС
С -> ε | +ДС | -ДС
Д -> РП | -Д | +Д
П -> ε | *РП | /РП
Р -> ч | (В)
Звенья цепочки ОПН опишем набором трёх типов:
1. Операнд - целые числа.
2. Одноместный оператор - однооп, это унарный минус и плюс.
3. Двуместный оператор - двуоп, это минус, плюс, умножить, делить.
Ниже представлено полное описание звена ОПН:
Соберём звенья в список, который будет представлять нашу ОПН. Для этого отметим 3 действия на отделах рисунка порядка:
Д1 - Создать хрон. Переменная хранящая звено до момента добавления в список.
Д2 - Запомнить. Помещаем встреченное звено в хрон.
Д3 - Добавить. Записываем в список ОПН.
Ниже показаны отделы и процедуры со встроенными действиями в разбор:
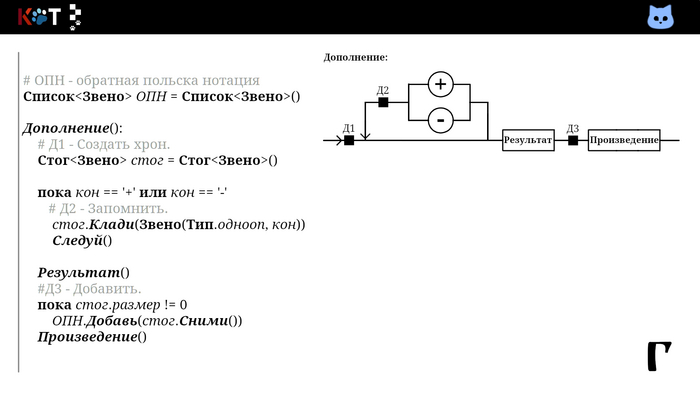
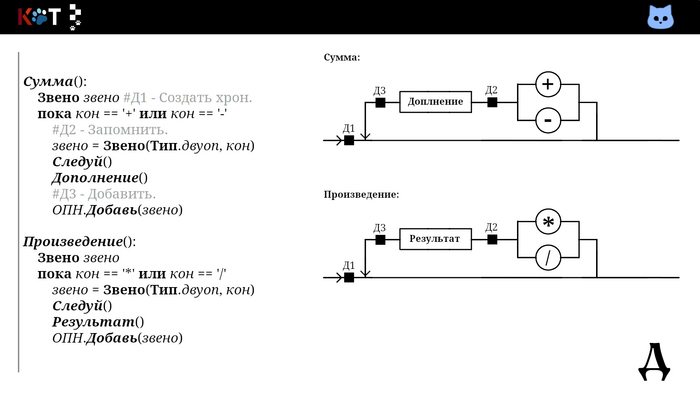
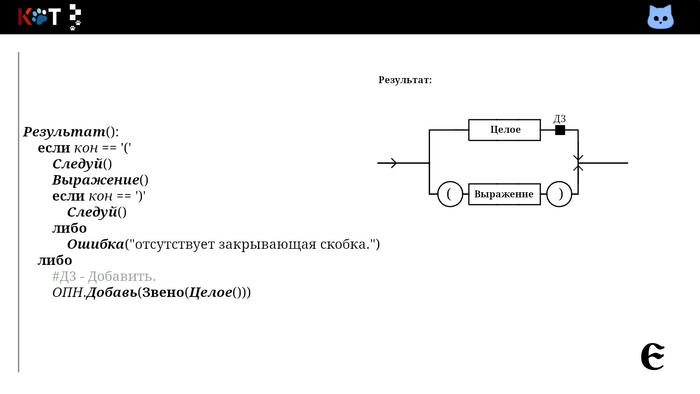
Так мы добавляем в первую очередь операнды, затем операторы в порядке их приоритетов. Всмотритесь в процедуру «Дополнениее». В качестве хрона используется стог (англ. stack), так как запоминаются несколько знаков сразу, их следует вспомнить в обратном порядке.
Осмыслим следующее: рекурсивный разборщик выступает теперь не только в качестве распознавателя, но и переводчика. Ведь мы получили цепочку принадлежащую другому формальному языку, который можно описать так:
Грамматика обратной польской нотации:
Г:В -> ч | П`П
П`-> чПО
П -> ВОП | ε
где:
В - ВЫРАЖЕНИЕ
О - ОПЕРАТОР
П - ПРАВОЕ_ПОДВЫРАЖЕНИЕ
П`- ПОДВЫРАЖЕНИЕ
ч - ЧИСЛО
Остановитесь на минутку, осмыслите.
Ниже изображена схема устройства вычисления ОПН - Стог-машина (Stack machine), а на следующем её описание. Для примера использована ОПН:
1 2 3 * + 4 -
Которая получена из инфиксной записи:
1 + 2 * 3 - 4


Стог-машина состоит из:
Стога - в котором хранятся промежуточные значения.
Набора двухместных и одноместных операций.
Движка - который читает ОПН, управляет стогом и обращается к набору операций.
ОПН обладает свойством: действия применяются последовательно при её чтении, на чём и основана работа стог-машины:
Если звено операнд, то кладём число в стог.
Если звено однооп, снимаем верхнее число обрабатываем, итог кладём в стог.
Если звено двуоп, снимаем два верхних числа и применяем операцию. Причём первое значение операции - второе верхнее, а второе - первое верхнее. Итог кладём в стог.
По окончанию чтения ОПН, итог вычисления оказывается на дне стога, одним.
Не стоит думать, что рассмотренный способ единственный для получения ОПН. Есть так же алгоритм Дейкстры перевода выражения в ОПН, но я не знаю стоит ли его разобрать или сразу перейти к обсуждению включения действий в «Провидца», ранее нами рассматриваемого.
Поэтому решение будет зависить от вас:
Ну на это всё, быть добру, хорошего настроения. Подписывайся. =)
Точно! Для любознательных и внимательных читателей, ещё одна не позиционная система счисления.
Предыдущая статья: Обещанная реализация КА и попытка создать таблицу переходов не детерминированному автомату. в vk.com
Что же давайте, ещё раз обратимся к нашему НКА и всё таки составим таблицу, в которую будем вписывать не к какому состоянию требуется перейти, а в какое состояние мы можем перейти, будем заполнять множеством состояний. Предоставляю граф и таблицу:
Символ Ø обозначает, что наш автомат завершил работу и более не принимает символов. Если мы продолжаем читать из потока, тогда нам следует перезапустить автомат для обработки уже следующей цепочки.
Приступим к алгоритму. Построим новый автомат на базе состояний нашего НКА. Состояния нового автомата будут иметь названия составляющие все возможные сочетания из множества состояний НКА по k, где k у нас будет меняться от 1 до максимального кол-ва. То есть в нашем случае до 3 из множество {S, B, K } это S, B, K, SB, SK, BK, SBK.
Состояния нового автомата в чьи имена попали, обозначения конечного состояния НКА, тоже становятся конечными: K, SK, BK, SBK. А начальное состояние не меняется S.
Теперь нам остаётся задать переходы по каждому символу, соблюдая следующее: Из каждого состояния N нового автомата направим не более чем один переход, помеченный данным символом, в такое состояние, которое соответствует множеству состояний НКА, в которые есть переходы по этому символу хотя бы из одного состояния НКА, образующего N.
Вот так:
Давайте построим для него граф:
У нас получился ДКА, только в нём есть состояния в которые мы никогда не попадём. Поэтому данный ДКА следует минимизировать, алгоритма минимизации возможно коснусь в последующих статьях. Но можно выделить две вещи, когда следует минимизировать ДКА, когда у нас «мертвые» состояния и когда состояния повторяют одно и то же действие. Вот так будет выглядеть результат минимизация получившегося ДКА:
Переименуйте BK в B и узнаете уже рассмотренный нами ДКА.
З. Ы. Для построения графов в этот раз использовал эти инструменты https://www.graphviz.org/download/ и можно web-версию использовать http://www.webgraphviz.com/. Следующая статья будет посвящена синтаксическим диаграммам автоматного языка. Не забывайте подписываться, если вам это интересно.=)
Предыдущая статья: Конечные автоматы, что там внутри? в vk.com
Как-то никто не голосует, поэтому решил выпустить раньше, язык реализации выбрал на своё усмотрение, посмотреть можно здесь. Пример основан на автомате из прошлой статьи.
Давайте попробуем создать таблицу переходов для этого автомата:
Как-то не особо получается верно? Нам не совсем-то понятно когда переходить в состояние K, мы как-будто застряли в неопределенности. Когда приняли символ a оставаться в состоянии B или переходить уже к другому? Данные типы автоматов называются не детерминированные конечные автоматы или просто НКА, они обладают особой приметой, то что на один и тот же принятый символ в одном состоянии есть более одного варианта перехода. И всё таки мы можем написать для него функцию перехода, добавив какие нибудь условия, например проверять не последний ли это символ. Что же получается я слукавил в прошлый раз? И да и нет, жертва для более наглядного, постепенного объяснения. Да - потому-что функцию перехода можно реализовать разными способами. Нет - потому-что это частный случай реализации детерминированных конечных автоматов или просто ДКА, когда каждый его переход однозначен. ДКА - гораздо эффективнее НКА и у меня хорошие новости:
Теорема Клини. Для каждого НКА можно построить ДКА, допускающий тот же язык.
В следующей статье мы рассмотрим алгоритм преобразования НКА в ДКА, не забывайте подписываться. Все здоровья и удачи.
Предыдущая статья: Графы автоматных грамматик. Что же, начинаем знакомиться с конечными автоматами? в vk.com
Если вы ознакомились со всеми прошлыми статьями, тогда вы готовы воспринять следующую информацию, я старался максимально кратко со всей ясностью подготовить вас, так-что попрошу вас заново перечитать. Приступаем, знакомимся с формулой конечного автомата:
A = (N, T, P, S, F)
Напоминает уже знакомую вам формулу грамматик? Давайте по порядку:
N - конечное множество состояний автомата, тот самый вспомогательный алфавит, плюс два или одно дополнительных состояния K и E, где E состояние ошибки и K дополнительное конечное состояние, если оно требуется.
Т - алфавит который принимает конечный автомат или тот самый основном алфавит грамматики.
P - функция переходов состояния автомата, принимает в себя текущее состояние автомата и подающий символ на рассмотрение, строится на основе правил вывода грамматики, ниже мы остановимся подробнее.
S - начальное состояние автомата.
F - множество конечных состояний автомата.
Ещё вы можете найти следующую формулу:
A = (N, T, O, δ, λ, F)
Где δ - функция переходов состояния автомата и записывают её так
δ : N × T → N означает что берется пара значений, одно из множества N, а другое из множества T и возвращает значение из множества N.
И λ - функция выходов, записывается λ : N × T → O , собственно O - означает выходной алфавит, или грубо говоря переводной. Например, сочтём за символы два слова, английское Hello из принимаемого алфавита и русское Привет из выходного алфавита, и во время работы автомата при некотором состоянии («контексте предложения»), принимает Hello и переводит его в Привет, ведь вполне может что в другом состоянии («контексте предложения») он может перевести его в Здравствуйте! =) Дальше повествование будет, только о автомате распознавателе, то есть без функции выходов, который описан выше, просто общий принцип функции переходов и выходов сильно не отличается.
Возьмем грамматику, я надеюсь уже любимого, языка идентификаторов:
G: S → aB
B → aB | bB | ε
И построим её граф.
Все верно, граф грамматики это же и отображение конечного автомата, который принимает язык порождаемый грамматикой. Теперь остановимся по подробней на функции перехода на примере этого автомата, для этого создадим таблицу переходов.
В таблице, жирным курсивом, отмечено состояние B, так как оно входит во множество конечных состояний и если автомат закончил принимать символы в одном из таких состояний, говорят что он принял данную цепочку. Так же вы видите состояние E, обычно его не отображают на графе, по одной просто причине, все пути веду в Рим к ошибке, когда подается символ не подходящий к состоянию или не входящий в алфавит который принимает автомат. Собственно наша функция обращается к этой таблице и переводит автомат, в то состояние которое получила из таблицы. Как-будто играет в морской бой, только с ответами ошибка, не ошибка.
Наверное вы заметили, что граф конечного автомата в прошлой статье и описанный в этой отличаются, хотя они принимают один и тот же язык? Об этом я расскажу в следующий раз, но перед этим я бы хотел показать вам программную реализацию КА на одном из языке программирования, на каком бы вы предпочли? Решение будет по результатам 3-его дня, после публикации статьи.
Опрос в vk.com у пикабушки нету =(
З. Ы. Подписывайтесь! =)
Предыдущая статья: Эквивалентность и однозначность грамматики или почему иногда 2+2*2=8? в vk.com
Рекомендую перечитать прошлые статьи, повторение мать учения. А пока, просто напомним себе как выглядят правила для автоматных грамматик:
A → aB
A → a
A → ε
где A и B вспомогательные символы, a - основной символ и ε - пустая цепочка.
С помощью этих трех правил легко отобразить грамматику языка с помощью направленного графа, для этого потребуется придерживаться следующего:
1) Каждый вспомогательный символ отображается узлом с названием этого символа.
2) Правила вида A → a порождают дугу (направленное ребро) графа от узла A к дополнительному узлу K, где K - конечный узел, дуга помечается названием основного символа a.
3) Правила вида A → aB, так же как во втором пункте, только к узлу B.
4) Узел начального вспомогательного символа помечается стрелкой.
5) Дополнительный узел K и узлы вспомогательных символов для которых соблюдается правило A → ε, помечаются двойным кружком, как конечные узлы.
Давайте построим граф уже известного нам языка идентификаторов, только воспользуемся его эквивалентной автоматной грамматикой, так как прошлый раз мы использовали КС-грамматику. Вот смотрите:
G: S→ a
S → aB
B → a
B → b
B → aB
B → bB
Следуя по направлению дуг, мы можем генерировать сколько угодно много цепочек входящие в наш описанный язык. Вот так.
А как же КА, спросите? Про это мы поговорим в следующий раз, но уже это должно натолкнуть вас, как он работает. Подписывайтесь, чтобы не пропустить продолжение.
Предыдущая статья: Задача разбора, для чего она нужна? Или что такое parsing? в vk.com
Рассмотрим следующую грамматику:
G: E → E + E | E – E | E * E | E / E | x
Данная запись краткая, в ней описаны только правила вывода. Собственно стартовым вспомогательным символом является E, а основные символы уже учтены в правилах это {+, -, *, /, x}, роль x заключается в обозначении любого числа.
Давайте попробуем построить дерево вывода цепочки x + x * x, но сперва запишем вывод:
E => E + E => E + E * E => x + E * E => x + x * E => x + x * x
Ещё можно поступить следующим образом:
E => E * E => E + E * E => E + E * x => E + x * x => x + x * x
Данные выводы различаются направлением построения выражения, соответственно имеют название левосторонний вывод и правосторонний вывод.
Что мы наблюдаем? Первое то, что грамматика выдает для выражения x + x * x два разных дерева вывода. На изображении, ниже уже привычного нам дерева, выведены редуцированные (упрощенные) деревья, такие деревья называют семантическими деревьями. Так если мы обойдем каждый узел рекурсивно и выполним действие предписывающее нашему знаку, мы получим разные результаты. То есть будем вычислять от листьев к корню, узел x будет означать просто вернуть число, если x = 2, то первое вариант выдаст нам 8, а второй 6. Такие типы грамматик являются неоднозначными.
Грамматика называется однозначной, если любой её сентенции (предложению) соответствует единственное дерево вывода, при правостороннем и левостороннем построении.
Попробуем исправить неоднозначность, рассмотрим другую грамматику со вспомогательным символом X, который будет обозначать операнд.
G: E → X | E + X | E – X | E * X | E / X
X → x
Построим выводы для той же цепочки x+x*x
E => E * X => E + X * X => E + X * x => E + x * x => X + x * x => x + x * x
или
E => E * X => E + X * X => X + X * X => x + X * X => x + x * X => x + x * x
От неоднозначности данная грамматика избавлена, но вот семантическое дерево не верно, не соответствует общепринятому в математике, сперва умножаем потом прибавляем. Возьмем другую, где T будет означать слагаемые и М - множители.
G: E → T | E + T | E – T
T → M | T * M | T / M
M → x
Разложить выражение x + x * x в данной грамматике попробуйте сами и убедитесь в однозначности данной грамматики.
Теперь можем немного подытожить, не смотря на то что все три рассмотренные грамматики являются разные по своей структуре и могут нести в себе разную семантику, они порождают один и тот же язык.
Грамматики называются эквивалентными, если порождают один и тот же язык.
Ту би континуе… Не забывайте подписываться. =)
Приношу извинения, за ошибки в выводах цепочек.
Левосторонним выводом называется вывод при котором заменяются в первую очередь левые неконечные символы.
Правосторонним выводом называется вывод при котором заменяются в первую очередь правые неконечные символы.
Исправления для первой грамматики, левосторонний вывод:
E => E * E => E + E * E => x + E * E => x + x * E = > x + x * x
Правосторонний вывод:
E => E + E => E + E * E => E + E * x => E + x * x => x + x * x
Исправления для второй грамматики, левосторонний вывод:
E => E * X => E + X * X => X + X * X => x + X * X => x + x * X => x + x * x
Правостороний вывод:
E => E * X => E * x => E + X * x => E + x * x => X + x * x => x + x * x
Сею голову пеплом, мне стыдно.
Предыдущая статья: Дерево вывода предложения (сентенции) грамматики. Синтаксическое дерево. в vk.com
Ответ, по поводу к какому языку относилась грамматика из прошлой статьи: Барабанная дробь!!!! Языку идентификаторов. Вместо a подставляйте любой символ из алфавита {A, … Z, a, … z, А … Я, а, …, я} и вместо b из алфавита
{ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 }. Таким образом вы получите типичный синтаксис любого языка программирования относящееся к названию переменных.
Собственно таким образом грамматика задает синтаксис языка, порядок языка, место каждого вашего символа, а если этот порядок нарушается, то значит данная цепочка (предложение, сентенция) , не относится к вашему языку. Вот над выяснением принадлежит ли некая цепочка символов к языку заданной грамматики и отвечает решенная задача разбора, но так же преследует цель выявлении структуры цепочки, семантики языка.
Так что же такое задача разбора? Очевидно, если вы прочли прошлую статью:
Задачей разбора является восстановление дерева вывода для заданной цепочки символов.
Повторюсь, ничто иное как построение вывода для заранее заданной цепочки, и чтобы наглядно вам продемонстрировать разбор сыграем в домино Де Ремера. За основу правил возьмём всю ту же грамматику G = ({a, b}, {S, A, B}, {S → AB, A → aA | a, B → bB | b}, S), создадим кости соответствующие правилам вывода:
Кости правил
Возьмем всю ту же самую цепочку aaabb и добавим в нашу игру ещё костей с этими символами и разложим их:
Начало игры
Вы обратили внимание на формы костей? Да, верно, наша цель, собрать дерево так чтобы подошли к нашим половинкам нужные кости правил, вот так:
Конец игры
Каким образом мы можем восстановить дерево? Ну первое что бросается в глаза, это в каком направлении мы будем подбирать кости правил. Подход решения от стартового вспомогательного символа к основным называется нисходящим разбором, в обратном же направлении восходящим разбором. И так же от левых символов левосторонним, а от правых правосторонним. Примеры:
Левосторонний нисходящий разбор.
Правосторонний восходящий разбор.
Это мы определили алгоритмы разбора по направлениям, но так же в ходе решения вы столкнетесь с тем какого характера будет алгоритм. Если вы будете ставить кость правил и вам не приходится её заменять, поздравляю вы подобрали хороший алгоритм и он детерминирован, а иначе если приходится заменять кость правил, то такой алгоритм не детерминирован.
Значение слова детерминация происходит от лат. determinatio — предел, заключение, определение, что означает определенность, однозначность, в нашем случае мы говорим о завершённых ходах, о том что всякое поставление кости на своём месте.
На этом тема закрыта, в следующий раз расскажу почему же бывает так, что 2+2*2 = 8?
Предыдущая статья: Хомски и его иерархия грамматик.
Посмотрите на следующую грамматику:
G = ({a, b}, {S, A, B}, {S → AB, A → aA | a, B → bB | b}, S)
| - означает ИЛИ, к пример A можно заменить на aA или просто a.
Кстати как вы думаете, какой язык описывает эта грамматика? Ответ будет в следующей статье, пока поразмышляйте над этим, а теперь к делу.
Давайте выведем какое-нибудь предложение данной грамматики:
S => AB => aAB => aAbB => aaAbB => aaabB => aaabb
Теперь построим дерево вывода, корнем нашего дерева будет стартовый вспомогательный символ, так как с него начинается вывод. Листьями, конечными узлами, окажутся символы основного алфавита, а связующими узлами будут вспомогательные символы. Дерево строить будем последовательно вставляя узлы в том порядке в каком мы подменяем символы согласно правилам.
Что же, можно сказать, всякий вывод предложения грамматики, порождает дерево, по крайней мере в неявном виде. Как вы думаете как называется обратная задача? Когда дано некое предложение грамматики например тоже самое aaabb и требуется восстановить дерево вывода.
Об этом в следующей статье…