Языковые эксперементы
7 постов
![Хайку код[т]](http://s15.pikabu.ru/images/series/2024/09/10/1725922956197399959.png)
Закреплено
Обратная польская нотация, получение и вычисление
Предыдущая статья: Включения действий при разборе и итог пройденных тем в vk.com
Статья для повторения: От перепутья к перепутью, часть вторая: Разбор языка арифметики
В привычной нами записи выражения, знак операции (далее оператор) записываются между значениями (далее операндами):
а + б
Такая форма называется инфиксной (калька - вкрепной).
Так же используется префиксная (докрепная) запись, когда операторы пишутся до операндов:
+ а б
и постфиксная (закрепная) запись, когда операторы пишутся за операндами:
а б +
Ниже показаны ещё примеры:
Префиксная и постфиксная запись также именуются прямая и обратная польская нотация (далее ОПН), в честь её изобретателя польского логика Яна Лукасевича. Отличительная их черта, то что в них не используются скобки для обособления вычисления.
Получение ОПН из инфиксной записи
Используем рекурсивный спуск по рассмотренной нами грамматике, где в качестве чисел целые без знака:
Грамматика с унарным минусом и плюсом:
Г: В -> ДС
С -> ε | +ДС | -ДС
Д -> РП | -Д | +Д
П -> ε | *РП | /РП
Р -> ч | (В)
Звенья цепочки ОПН опишем набором трёх типов:
1. Операнд - целые числа.
2. Одноместный оператор - однооп, это унарный минус и плюс.
3. Двуместный оператор - двуоп, это минус, плюс, умножить, делить.
Ниже представлено полное описание звена ОПН:
Соберём звенья в список, который будет представлять нашу ОПН. Для этого отметим 3 действия на отделах рисунка порядка:
Д1 - Создать хрон. Переменная хранящая звено до момента добавления в список.
Д2 - Запомнить. Помещаем встреченное звено в хрон.
Д3 - Добавить. Записываем в список ОПН.
Ниже показаны отделы и процедуры со встроенными действиями в разбор:
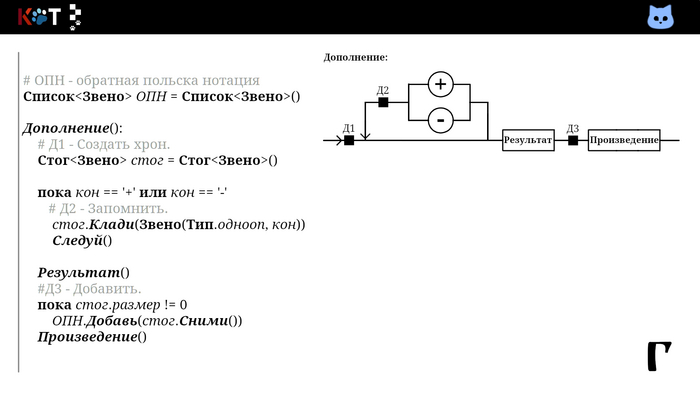
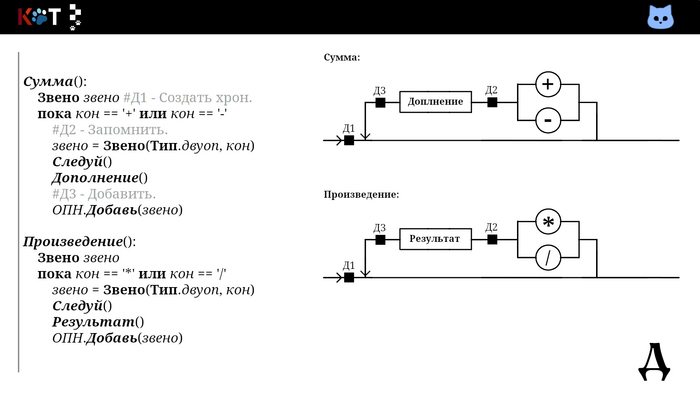
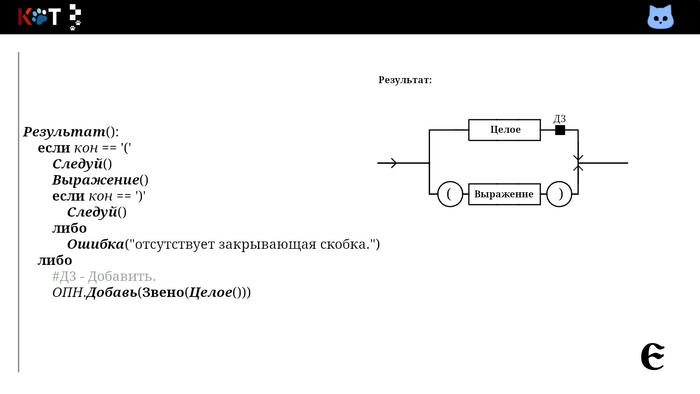
Так мы добавляем в первую очередь операнды, затем операторы в порядке их приоритетов. Всмотритесь в процедуру «Дополнениее». В качестве хрона используется стог (англ. stack), так как запоминаются несколько знаков сразу, их следует вспомнить в обратном порядке.
Осмыслим следующее: рекурсивный разборщик выступает теперь не только в качестве распознавателя, но и переводчика. Ведь мы получили цепочку принадлежащую другому формальному языку, который можно описать так:
Грамматика обратной польской нотации:
Г:В -> ч | П`П
П`-> чПО
П -> ВОП | ε
где:
В - ВЫРАЖЕНИЕ
О - ОПЕРАТОР
П - ПРАВОЕ_ПОДВЫРАЖЕНИЕ
П`- ПОДВЫРАЖЕНИЕ
ч - ЧИСЛО
Остановитесь на минутку, осмыслите.
Вычисление ОПН
Ниже изображена схема устройства вычисления ОПН - Стог-машина (Stack machine), а на следующем её описание. Для примера использована ОПН:
1 2 3 * + 4 -
Которая получена из инфиксной записи:
1 + 2 * 3 - 4
Стог-машина состоит из:
Стога - в котором хранятся промежуточные значения.
Набора двухместных и одноместных операций.
Движка - который читает ОПН, управляет стогом и обращается к набору операций.
ОПН обладает свойством: действия применяются последовательно при её чтении, на чём и основана работа стог-машины:
Если звено операнд, то кладём число в стог.
Если звено однооп, снимаем верхнее число обрабатываем, итог кладём в стог.
Если звено двуоп, снимаем два верхних числа и применяем операцию. Причём первое значение операции - второе верхнее, а второе - первое верхнее. Итог кладём в стог.
По окончанию чтения ОПН, итог вычисления оказывается на дне стога, одним.
В заключении
Не стоит думать, что рассмотренный способ единственный для получения ОПН. Есть так же алгоритм Дейкстры перевода выражения в ОПН, но я не знаю стоит ли его разобрать или сразу перейти к обсуждению включения действий в «Провидца», ранее нами рассматриваемого.
Поэтому решение будет зависить от вас:
Ну на это всё, быть добру, хорошего настроения. Подписывайся. =)
Точно! Для любознательных и внимательных читателей, ещё одна не позиционная система счисления.
Показать полностью
8
1
