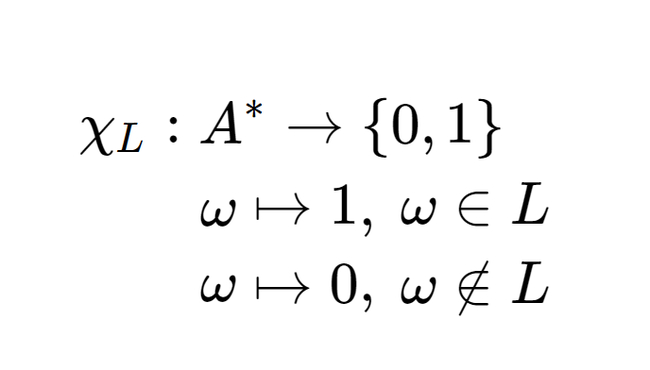В 2000 году Математический институт Клэя определил 7 математических задач, решение которых не могли найти в течение многих лет. За решение каждой из них была назначена награда в размере 1 миллиона долларов. Эти 7 задач известны как «задачи тысячелетия», и на сегодняшний день только одна из них была решена — гипотеза Пуанкаре. В этой статье пойдет речь о вопросе равенства классов P и NP, ответ на который может сильно повлиять на всю IT-сферу.
Вспомогательные детали
Равенство P и NP классов отсылает нас к теории алгоритмов, а именно к классам сложности. Первое, с чего стоит начать, это то, что классы P и NP классифицируют языки, а не задачи. Пока что это звучит довольно абсурдно, поэтому для понимания разберемся в некоторых деталях.
Алфавит
В теории алгоритмов алфавит — это непустое конечное множество символов. Набор символов ASCII - это алфавит. {0 , 1} - тоже алфавит. {} - такое множество нельзя назвать алфавитом, поскольку оно пустое, а множество целых чисел Z нельзя назвать алфавитом, поскольку оно бесконечно.
Слово
Допустим, мы имеем алфавит. Назовем его A. Тогда словом над алфавитом А является упорядоченное соединение конечного числа символов. Например, 110110 — это слово над алфавитом {0 , 1}, а «habr» - слово над алфавитом ASCII символов. Но число пи не будет словом над алфавитом { . , 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9}, так как число пи из символов данного алфавита не будет конечным. Над любым алфавитом существует пустое слово, обозначать его будем символом e. Слова обладают такой характеристикой, как длина, т. е. количество символов в нем. Обозначать длину слова будем в виде модуля. Длина вышеупомянутого слова |110110| = 6.
Язык
Возьмем уже упомянутый алфавит А. Пусть множество А* содержит все слова над алфавитом А, а множество А+ также содержит все слова над А, за исключением e (значки + и * взяты из регулярных выражений). Множество Аn содержит все слова длины n. Для любого алфавита множества А* и А+ будут бесконечными (можно составить бесконечное количество слов разной длины для любого алфавита). Для алфавита А = {0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9} множество А2 будет представлять набор из двузначных чисел.
Пусть А — алфавит и L ⊆ А*, тогда L называется языком над А. Для любого алфавита пустое множество и А* являются тривиальными языками. При этом пустое множество часто называют пустым языком. Однако не стоит путать пустой язык и язык, содержащий пустое слово e, — они различны. Языки могут быть как бесконечными, так и нет, но обязательно счетными. Т. е. множество всех действительных чисел языком нельзя назвать, т. к. такой набор является неисчисляемым.
Абстрактный исполнитель
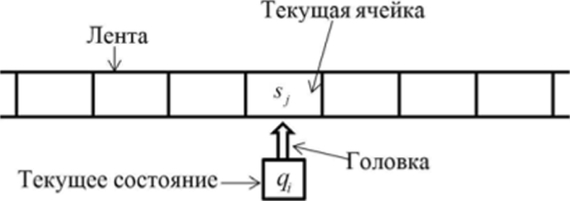
Говоря про абстрактный исполнитель, чаще всего имеют в виду машину Тьюринга, поэтому в дальнейшем под АИ будем подразумевать именно её. Итак, машина Тьюринга имеет неограниченное линейное хранилище, сгруппированное в ячейки. Каждая ячейка может содержать ровно один символ алфавита в любой момент времени. Вдоль ячеек идет считывающая головка, имеющая конечное число состояний. За одну итерацию она может считать значение только одной ячейки, переписать её значение, изменить свое состояние и перейти на одну позицию вправо/влево.
Устройство машины Тьюринга
На основе машины Тьюринга определим так называемую разрешающую машину над языком. Для начала введем определение характеризующей функции X(w). Функция X определяет, принадлежит ли слово w языку L. Если да, то значение функции равно «1»; если нет, то «0». Формально это можно записать так:
Разрешающей машиной D для языка L называется такая машина, которая для каждого w∈A вычисляет характеризующую функцию X(w) за конечное время.
В дополнение к разрешающей машине идет верификатор. Машина V, которая принимает слова w и c и выводит 0 или 1 после конечного числа шагов, называется верификатором для L, если она обладает следующими свойствами:
- выводит 1, только если w входит в язык L;
- для любого w в языке L существует такое c, что V(w,c) = 1.
В данной машине буквой с называется свидетель или сертификат. Фактически, верификатор также проверяет, входит ли какое-либо слово в язык, однако делает это с учетом свидетеля, который ускоряет проверку. Например, возьмем число 182652. Входит ли оно в язык простых чисел, т.е. является ли оно простым. Без компьютера это будет довольно сложно проверить, однако имея сертификат — числа 186 и 982, произведение которых дает в результате число 182652, - задача проверки сильно упрощается. Фактически, свидетель - это любая информация, упрощающая проверку вхождения слова в язык.
Классы сложности и формулировка проблемы
Окей, мы рассмотрели несколько понятий. На первый взгляд, все это больше походит на лингвистику: алфавиты, слова, языки… Причем тут задачи? Чтобы ответить на этот вопрос, обратимся к понятию задача разрешимости (англ. Decision problem). Это такой вопрос (сформулированный в формальной системе), требующий ответа «да» или «нет», зависящего, возможно, от значений некоторых входных параметров. Например, «является ли данное натуральное число x простым?» или «даны два числа: x и y; делится ли x на y?« Метод решения в виде алгоритма называется разрешающей процедурой. Теория вычислимости имеет дело в основном с задачами разрешимости и приведенные выше конструкции наглядно соотносятся с таким типом задач: так разрешающая машина над языком является формализацией разрешающей процедуры. Но как же быть с задачами, такими как задача коммивояжера? На них нельзя дать бинарный ответ. В таких случаях применяют приемы приведения к версии decision problem. В случае коммивояжера проблема по-новому формулируется так: «существует ли маршрут не длиннее, чем заданное значение k?»
В класс сложности NP входят все языки L, для которых существует такой верификатор, что для каждого (w,c) время его работы полиномиально. Иными словами, NP включает в себя задачи разрешимости, для которых при подходящем сертификате для данного w мы быстро сможем удостовериться в том, что w действительно принадлежит L (ответ на вопрос можно довольно быстро проверить). Отсюда и название «верификатор». В качестве примера задачи в NP можно привести определение наличия в графе гамильтонова цикла. Сертификат в данном случае — последовательность вершин, образующих гамильтонов цикл.
Помимо этих классов можно выделить ещё 2: NP-hard и NP-Complete. Они основываются на приводимости одного языка к другому за полиномиальное время: пусть языки A и B — языки над одним алфавитом. Язык А будет приводимым за полиномиальное время к языку B, если существует такая функция f(w), что
w ∈ A ⇔ f ( w ) ∈ B,
- функция f может быть вычислена машиной Тьюринга за полиномиальное время.
Тогда в класс
NP-hard будут входить языки, к которым приводимы все языки в
NP (причем
NP-hard язык может входить в
NP, а может и нет), а в
NP-Complete те языки, которые являются одновременно
NP-hard и
NP. Примером
NP-Complete является язык
выполнимых булевых формул (SAT). Таким образом,
NP-Complete задачи образуют в некотором смысле подмножество «типовых» задач в классе
NP: если для какой-то из них найден «полиномиально быстрый» алгоритм решения, то и любая другая задача из класса
NP может быть решена так же «быстро».
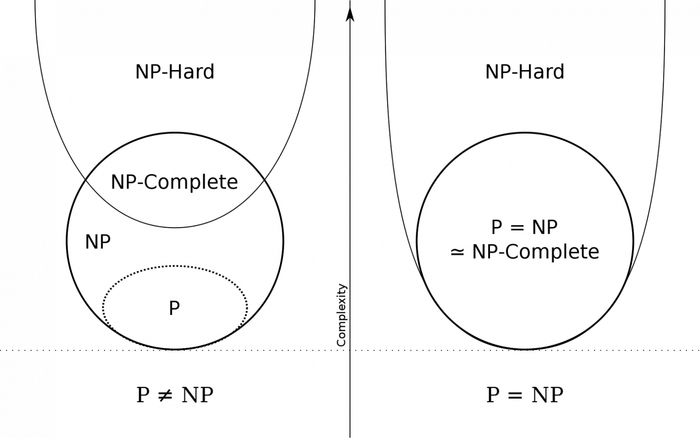
Отношение между классами при равенстве и неравенстве
Формулировка проблемы
Теперь, немного погрузившись в теорию алгоритмов, более конкретно обозначим проблему равенства данных классов. Итак, множество P входит в множество NP, но неизвестно, существуют ли языки, которые входят в NP и не входят в P. Что это означает на практике? Итак, простыми словами класс NP можно охарактеризовать как «трудно решить, легко проверить». Классическим примером задачи, входящей в NP, является задача коммивояжера, для решения которой на данный момент известен лишь один алгоритм — старый добрый перебор (мы не рассматриваем эвристические методы). Однако, получив ответ, его будет не так сложно проверить. Класс P же вобрал в себя те задачи, для которых существует эффективный алгоритм решения, позволяющий решать их за полиномиальное время. И равенство или, наоборот, неравенство этих классов пока не доказано. Если эти классы равны, то это будет значить, что для всех задач, которые сейчас решаются путем перебора или другим неэффективным методом, существует(-ют) полиномиальные алгоритмы. А если не равны, то придется смириться с неоптимальностью решения этих задач.
История
История проблемы равенства P и NP началась в 1928 году, когда Давид Гильберт сформулировал проблему, названную Entscheidungsproblem (нем. задача разрешения). Ее суть заключается в нахождении алгоритма, определяющего доказуемость данного утверждения из аксиом с использованием правил логики. По названию очевидно, что это задача является задачей разрешения (выводит «да» или «нет»).
В ходе решения этой проблемы потребовалось определить термины «алгоритм» и «вычислимая функция». В 1936 году Алонзо Чёрч и Алан Тьюринг независимо показали, что общее решение Entscheidungsproblem невозможно, предположив, что интуитивное понятие «эффективная вычислимость» соответствует вычислимости функции на машине Тьюринга. Эта гипотеза сегодня известна как тезис Чёрча-Тьюринга.
20 марта 1956 в письме к Джону фон Нейману Курт Гёдель впервые поставил вопрос о вычислительной сложности. Гёдель интересовался, можно ли получить доказательство теоремы (в математико-логическом смысле слова) за квадратичное или линейное время. К сожалению, письмо было обнаружено лишь в 1989 году и получило широкую огласку, когда Юрис Хартманис опубликовал перевод и комментарий.
Статья Алана Кобэма 1965 года под названием «The intrinsic computational difficulty of functions» является одним из первых упоминаний класса сложности P, состоящего из разрешимых за полиномиальное время задач. Тезис Кобэма-Эдмондса (известный также как расширенный тезис Чёрча-Тьюринга), названный в честь Алана Кобэма и Джека Эдмондса, утверждает, что любая разумная модель вычислений может быть выражена через другую модель с замедлением, не более чем полиномиальным по размеру входных данных. Кобэм предположил, что класс P может быть хорошим способом для описания множества реально вычислимых задач. Любая проблема, не содержащаяся в P, невозможна, но если задача реального мира может быть решена с помощью алгоритма, существующего в P, то такой алгоритм в конечном итоге будет открыт.
В 1965 году Юрис Хартманис и Ричард Стернс опубликовали статью «On the Computational Complexity of Algorithms», отмеченную премией Тьюринга. В ней даются более точные определения сложности алгоритма и класса сложности. Хартманис и Стернс определили класс сложности как совокупность всех задач, которые можно решить за установленные временные рамки. В их статье показано, что существует бесконечная иерархия классов сложности (например, задачи, для которых наиболее быстрый алгоритм имеет время, пропорциональное n, n log n, n^2, n^3, 2^n и т. д.), где небольшое увеличение временного интервала позволяет решать больше задач. Во второй статье Хартманис совместно с Филипом М. Льюисом показали, что подобная иерархия существует и для количества памяти (функция от размера входа) при решении задачи на машине Тьюринга.
В 1967 году Мануэль Блюм разработал аксиоматическую теорию сложности, которая основана на его собственных аксиомах (аксиомы Блюма), и получил важный результат — теорему об ускорении. До этого мы говорили по большей части о сложности алгоритма. Хотелось бы аналогичным образом определить и сложность задачи: например, какова сложность самого эффективного (по времени и емкости) алгоритма, решающего эту задачу. Теорема об ускорении гласит, что есть некоторые задачи, для которых не существует самого быстрого алгоритма, потому что любой алгоритм для такой задачи можно «ускорить», построив более быстрый алгоритм.
Точная формулировка проблемы равенства P и NP была представлена в 1971 году. Тогда американский ученый Стивен Кук и работавший независимо советский ученый Леонид Левин доказали, что существуют практически актуальные проблемы, которые являются NP-полными. В США Стивен Кук опубликовал статью «The complexity of theorem proving procedures», в которой формализовал понятия редукции за полиномиальное время и NP-полноты, а также доказал существование NP-полной задачи (задача выполнимости булевых формул, SAT). Теорема была независимо доказана Леонидом Левиным и, таким образом, получила название «теорема Кука-Левина».
В 1972 году Ричард Карп сделал рывок в знаменитой статье «Reducibility among Combinatorial Problems», в которой показал, что около 20 разнообразных задач из комбинаторики и теории графов, известных своей вычислительной трудностью, являются NP-полными.
В августе 2010 года Виней Деолаликар, работавший в исследовательском отделении Hewlett-Packard в Пало-Альто в Калифорнии, заявил, что разгадал загадку P vs NP. Он утверждал, что P не равняется NP, однако научное сообщество нашло в его доказательстве фатальную ошибку. В начале 2002 года SIGACT News провел опрос среди 100 ученых, задав им вопрос о равенстве классов NP и P. 61 человек ответили, что «неравны», 9 — «равны», 22 затруднились ответить и 8 сказали, что гипотеза не выводима из текущей системы аксиом и, таким образом, не может быть доказана или опровергнута.
К чему приведет решение проблемы
Окей, теория вычислимости, формализация алгоритмов и абстрактные математические теории — все это конечно интересно, но как решение проблемы равенства NP и P классов отразится на практике? На самом деле, алгоритмы для решения NP-задач используются каждый день во многих сферах. Например, в криптографии, криптовалютах, восстановлении поврежденных файлов, системах блокировки спама, оптимизации в логистике и т. д. Более эффективные решения могли бы значительно сэкономить время и деньги, так как мы пользуемся в основном эвристическими методами, дающими лишь приближенные решения.
Однако существует и обратная сторона монеты. Солидная часть криптографии (криптосистемы с открытым ключом, технологии доказательства выполнения работы в блокчейне, системы блокировки спама) основывается на предположении о неравенстве NP и P классов. Если окажется, что некоторые задачи, для которых, как считалось, не существует эффективных алгоритмов, можно решать быстро, то многие методы защиты устареют.
Может оказаться и так, что последствия решения окажутся не такими тривиальными, как это часто и бывает в математике. В качестве примера рассмотрим континуум-гипотезу о существовании мощности, меньшей континуума и большей мощности счетного множества. Оказывается, существование такого кардинала нельзя ни доказать, ни опровергнуть в аксиоматике ZFC. Так что мы вправе считать, что такие мощности бывают (впрочем, как и считать, что не бывают). Однако ясно, что мы не можем конструктивно построить соответствующее множество. Возможно, точно также окажется и с алгоритмами для NP-задач в случае равенства NP и P (к слову, некоторые математики в опросе SIGACT News так и ответили: гипотеза не выводима из существующей системы аксиом, то есть не может быть доказана или опровергнута).
Пока что существующих методов доказательств недостаточно для строго математического ответа, но не нужно терять надежду. В марте 2001 года Ричард Карп предсказал, что проблема будет решена молодым математиком (до 30 лет) с использованием подхода, о котором еще никто не думал. Стивен Кук заявил, что кто-нибудь предоставит убедительное доказательство в ближайшие 20 лет.