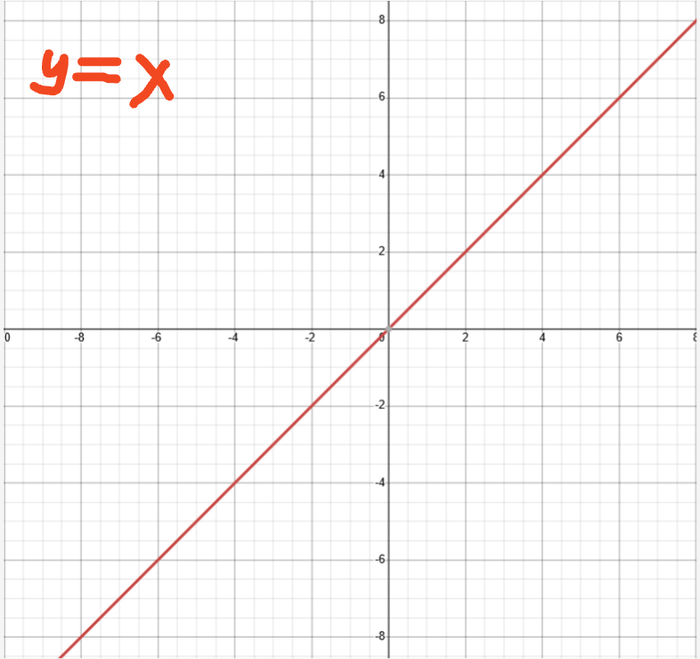
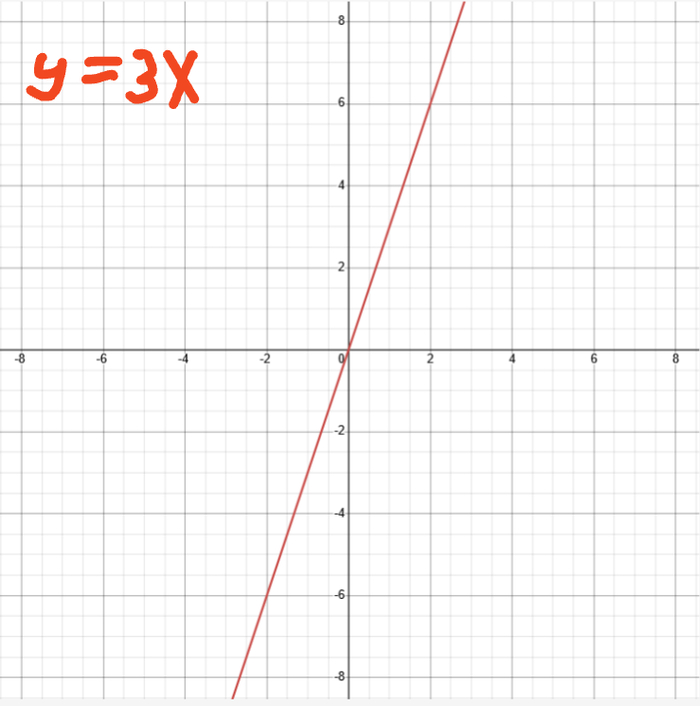
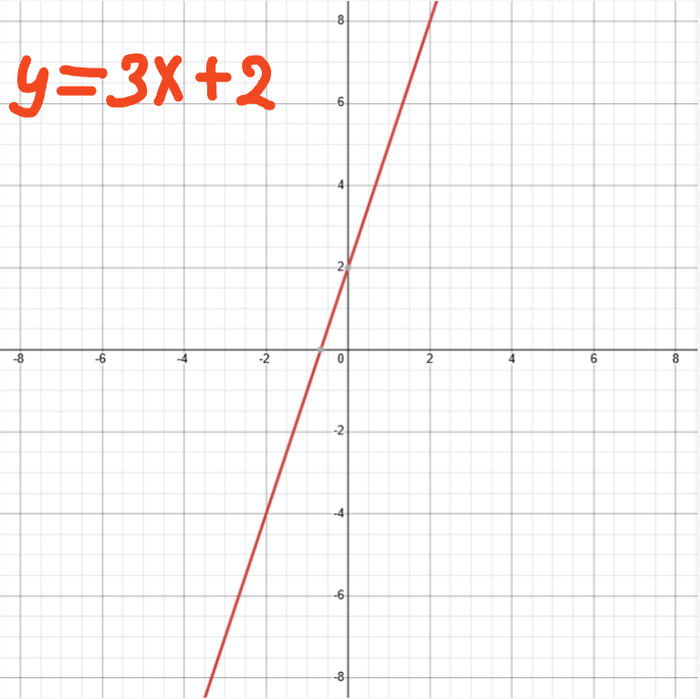
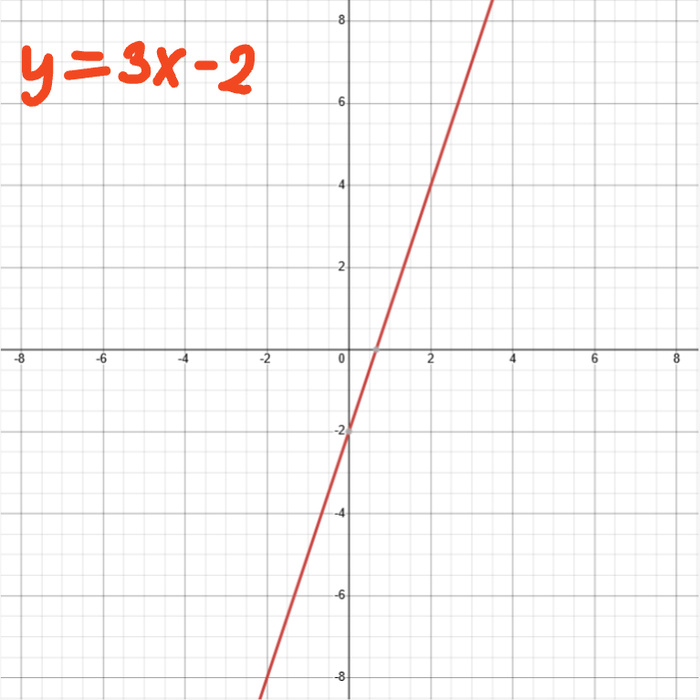
В рамках данной статьи я бы хотел предложить своё видение решений одной из самых важных, актуальных и сложных проблем современной науки и философии. Это проблема сущности сознания, в том числе и так называемая "трудная проблема сознания" по Д. Чалмерсу. Актуальности и даже можно сказать "хайпа", этой проблеме, помимо всего прочего, придают и исследования в области ИИ, постепенное внедрение ИИ во все сферы нашей жизни. Расскажу о собственных выводах, к которым пришел, много лет изучая философию в целом, философию сознания в частности, а также анализируя данные современных естественных наук и развитие передовых технологий.
Небольшое предисловие
Философией сознания я занимаюсь уже довольно давно и это одна из моих любимых и наиболее интересных для меня тем в философии и современной науке. В скором времени я планирую опубликовать также и собственное большое исследование со ссылками на авторитетные исследования, осуществленные у нас и за рубежом. А пока я бы хотел, не перегружая статью сносками и технической терминологией, сделать общий обзор основных выводов, к которым пришел лично я в ходе своих исследований.
Разумеется мои выводы не претендуют на истинность в последней инстанции. Я пишу эту статью скорее как приглашение к конструктивной дискуссии. Ранее здесь я уже делал небольшой обзор тех некоторых современных исследований, которые могут помочь нам пролить свет на природу сознания. Сейчас я бы хотел развить несколько выводов, опираясь на эти и другие исследования.
Для начала на всякий случай напомню, почему проблема сознания вообще так сложна и актуальна, и в чем заключается "трудная проблема сознания", сформулированная Д. Чалмерсом.
Дело в том, что на данном этапе развития науки сознание является несводимым к физикалистской картине мира. Иными словами, весь материальный мир, вся материальная Вселенная, описываемая естественными науками, представляет собой весьма самодостаточную, в некотором смысле замкнутую систему, для которой сознание в целом и субъективный опыт в частности не нужны. Для функционирования Вселенной в рамках всех физических, химических, билогических процессов сознание не требуется нигде, никогда и никому ни на каком этапе. И тем не менее, оно почему-то есть, и оно не вписывается в эту картину мира. Сознание - это как пятое колесо для физической реальности.
Да, ученые говорят, что раз сознание появилось, значит это было как-то обусловлено природой и необходимо с точки зрения эволюции. Но всё это - лишь предположения. Сознание не выводится из физической реальности. Оно ей буквально не нужно. То есть мы не объясняем сознание как бы неким естественным образом из всей эволюции природы, но вынуждены придумывать объяснения того, почему сознание оказалось эволюционно необходимо лишь потому, что сознание просто есть как факт.
Да, ученые также научились объяснять как определенные процессы в мозге связаны с сознательным опытом, но это как раз-таки "легкая проблема сознания", потому что в рамках таких исследований если еще не всё до конца понятно, то, по-крайней мере, ясен общий путь исследований и их методология. А вот вопрос о том, почему у определенных существ во Вселенной вообще в принципе есть сознательный опыт, почему физические, химические, биологические процессы сопровождаются субъективным опытом и чем он вообще является по сути - это как раз трудная, до сих пор нерешенная, проблема сознания.
Вкратце, элементы субъективного сознательного опыта в философии сознания принято называть "квалиа". Вкус кофе, ощущение красного цвета, восприятие музыки - всё это примеры квалиа. Удивительно то, что квалиа невозможно передать другому человеку и невозможно их формализовать. Да, из физики мы знаем, что длина волны красного цвета составляет примерно 650 нм. Но мы не можем знать, как эту волну видит другой человек. Вы и ваш друг, воспринимая такую волну, называете ее "красный цвет", но вы не можете знать, что именно видит ваш друг. Возможно тот цвет, который видит он, совершенно не похож на ваше восприятие красного. Но вы не можете посмотреть на красный его глазами, а ваш друг не может описать свое квалиа.
Да, человек безусловно может привести множество эпитетов для описания вкуса, цвета, звука, но все эти эпитеты - это его квалиа. Любые описания от другого человека вы считываете через свои собственные квалиа, поэтому через чужие описания вы, на самом деле, не можете понять, каковы квалиа другого человека в действительности. Отсюда берет свое начало и знаменитая статья Т. Нагеля "Что значит быть летучей мышью?". Название статьи говорит само за себя: мы можем изучить абсолютно все физические, химические, биологические факты о летучих мышах, но это не дает нам ровно ничего для понимания субъективного опыта (квалиа) этого существа.
Но вот к каким вывода, пытаясь ответить на вопросы о сущности квалиа и сознания, я пришел:
1) вероятно панпсихизм верен,
2) сознание, скорее всего, тесно связано с математикой и представляет собой определенную математическую структуру или имеет математическую сущность.
Первый вывод пока оставим в стороне. Скажу лишь в общем виде, что панпсихизм - это концепция, согласно которой сознание является универсальным и фундаментальным явлением природы. То есть оно присуще всему, примерно так же, как в Классической механике всему присуще нахождение в пространстве и во времени. Не стоит думать, что панпсихизм - это какая-то мистическая философия. Сегодня различные версии панпсихизма разделяют и разрабатывают академические ученые из сферы физики, математики и нейробиологии, а также многие философы, как тот же Д. Чалмерс.
Давайте сосредоточимся на втором выводе.
Код реальности
Я считаю, что квалиа - это способ, которым Вселенная или сама природа, если угодно, кодирует большие объемы данных. Мир вне нашего восприятия - это огромная совокупность объектов и явлений, которые мы не видим, потому что если бы мы их видели, то это была бы неоправданно большая нагрузка на мозг. Это было бы слишком, даже чересчур энергозатратно для эволюции. Мы не видим квантовые поля, элементарные частицы, волны, молекулы, темную материю и темную энергию, не воспринимаем звуки в определенном диапазоне и так далее, но ведь всё это есть. Реальность - это не совокупность предметов, которые мы видим. Реальность - это всё, что мы видим плюс всё, чего мы не видим и никак не воспринимаем в единой совокупности везде и сразу.
То есть атомы и молекулы, поля и волны - это не реальность какого-то иерархически более низкого или второстепенного уровня, чем тот, который мы воспринимаем. Это такая же реальность, как и всё остальное, что мы воспринимаем. Более того. Барионная материя (вещество), которую мы способны воспринимать в принципе, составляет меньшую часть от всей доступной нам Вселенной (примерно 5%). Но даже эту барионную материю мы не воспринимаем непосредственно полностью.
Мало того, что барионная материя - это 5% от доступной нам Вселенной, так в рамках этих 5% мы можем видеть непосредственно лишь то, что находится в очень узкой полосе видимого света, составляющей примерно 1% от всего электромагнитного спектра.
Всё это я говорю к тому, что реальность как бы переполнена огромными объемами данных, которые мы не можем воспринимать непосредственно, иначе наш "внутренний компьютер" был бы просто перегружен и не мог бы функционировать. И вот возможно, что природа и создает квалиа именно как способ удобного "кодирования" огромного объема данных. Эти данные как бы упаковываются в компактную форму, которую мы и называем "квалиа".
И ведь действительно, любое квалиа - это прежде всего математические данные:
форма - это длина, ширина, высота,
цвет и звук - это длина волны,
запах и вкус - это определенное количество атомов определенных химических элементов, которые различаются между собой так же количественно через вес атомного ядра и т.д.
вес, плотность предмета - это так же в конечном счете определенные числовые данные, математика.
Таким образом, любой предмет или явление - это единая совокупность различных математических данных, компактно упакованных в субъективный опыт.
И вот это как раз и подтверждается этим, этим и вот этим исследованиями, где ИИ кормят цифровыми данными, как например фМРТ мозга человека, воспринимающего или представляющего определенные образы, а ИИ через эти цифровые данные восстанавливает то, что видел или представлял человек. Иными словами, если квалиа - это код, то наш мозг с его сознательным восприятием - это "декодер", понимающий загруженный в него код как конкретный предмет с определенными качественными характеристиками, хотя фундаментально никаких предметов с их качествами не существует самих по себе, а существуют только квантовые поля, волны и энергии.
Вероятно природа создала много разных "декодеров", каждый из которых по-своему считывает и преобразует некий единый код реальности. Отсюда и биологическое понятие умвельта - субъективной картины мира того или иного существа. Собаки, люди, кошки, клещи, амебы - все видят мир по-разному, каждый живет в собственном умвельте, потому что у каждого существа стоит своя определенная "операционная система", по-своему считывающая и преобразующая код реальности. То есть каждая такая "операционная система" по-своему упаковывает большие объемы данных в квалиа, эти квалиа разные в разных умвельтах ("операционных системах"), поэтому мы и не можем узнать, что значит быть летучей мышью, ведь для этого нам нужен её декодер, её ОС. Или всё-таки можем?
Так каково же это - быть летучей мышью?
Опираясь на упомянутые выше исследования, а также на ряд других исследований и новостей о возможностях современных технологий (например, успехи чипов от Илона Маска, биосинтетический ИИ и т.п.), я думаю, что недалек тот день, когда мы сможем "увидеть" чужие квалиа и наконец понять, "что же значит быть летучей мышью". Технология по "перекодированию" чужих квалиа будет примерно следующей.
Определенные образы человека или другого живого и сознательного существа считываются и оцифровываются как в тех же экспериментах с фМРТ, затем эти цифровые данные направляются в чип, вживленный в мозг человека (как те же чипы от Илона Маска) и через этот чип в мозг идет раскодирование чужих квалиа и вы начинаете чувствовать, воспринимать и понимать как видит цвета ваш друг или как видит мир летучая мышь.
Возникает вопрос, как проверить достоверность такого восприятия? Технология такой экспериментальной проверки тоже может быть разработана и возможно будет выглядеть примерно следующим образом. Вам вживляют чип. Через чип вы видите красный цвет так, как его видит ваш друг. Затем ваше видение красного через призму чипа, настроенного на квалиа вашего друга снимается при помощи того же фМРТ, оцифровывается и направляется в чип, вживленный в мозг вашего друга и ваш друг как бы видит то, что видели вы, смотря на мир глазами вашего же друга. Таким образом, ваш друг как бы проверяет, валидирует: действительно ли вы видели красный именно так же как и он.
Теперь давайте вернемся к первому моему выводу о панпсихизме.
Почему панпсихизм?
Как видно из вышесказанного, я считаю, что сознание носит математический характер. А саму математику, как вы могли заметить из других моих статей, я считаю не просто языком науки, но онтологической реальностью. То есть, есть математика как язык со своими символами, а есть математика как объективная реальность, для которой мы и придумали все эти символы. Приведу основные аргументы, почему вслед за Пифагором, Платоном и М. Тегмарком, я считаю математику онтологической реальностью:
1) Феноменальная эффективность в научном познании мира. Математика - это не язык, придуманный людьми. Обычные языки, как немецкий, английский или русский, не позволяют нам совершать открытия и находить то, что ранее было скрыто, узнавать, что происходит на субатомном уровне или далеко во Вселенной. Математика позволяет. Формулы и символы - это язык. Но сама математика - не язык, так как она позволяет априори открывать нечто, что лишь через много лет удается подтвердить экспериментально. Математика не описывает мир внешне. Она задает сами законы, по которым мир живет.
2) Универсальность математики. Математика действует одинаково во всех уголках известной Вселенной, для всех людей и культур и во все времена. Она в этом смысле предельно объективна, так как не зависит буквально ни от чего, кроме самой себя.
3) Фундаментальная основа мира должна быть больше и сложнее всего того, что мы видим в мире. Если в мире есть материя и идея, основа должна быть вне их. Если в мире есть причины и следствия, основа должна быть беспричинной. Если в мире есть пространство и время, основа должна быть независимой от них. Математика идеально подходит под все эти условия. Более того, только математика под них и подходит. Какова причина того, что 2+2=4?
4) Независимость от опыта и разума. Математические объекты, константы и законы существует и действуют независимо от того знаем мы о них или нет, открыли мы их или нет. Как сказал однажды А.М. Семихатов: "Я не понимаю, каким образом вся Вселенная во всех уголках знает о собственных константах". Число пи существует и играет свою роль в площади окружности, независимо от наших знаний об этом. Как и теорема Пифагора. То есть сами соотношения между длиной окружности и её диаметром, между катетами и гипотенузой абсолютно никак не связаны с нашей осведомленностью о них.
5) Некоторые явления, как например, волновая функция или квантовое поле описываются только математикой. Мы не можем ни визуализировать и никак иначе достаточно точно передать, что происходит на Квантовом уровне. Математика может. Волновая функция и квантовое поле не существуют как нечто осязаемое. Они существует лишь как математические объекты, но лежат в основе реальности.
6) Асимметрия между математикой и другими науками. Другие науки (например, биология, химия, социальные науки) зависят от наблюдений и экспериментов, тогда как математика основана на логических доказательствах и аксиомах. Это делает математику более универсальной и фундаментальной, чем другие науки поскольку она не зависит от эмпирических данных.
7) Замкнутость на саму себя. Если все другие науки вынуждены обращаться к математике и часто доказывают или опровергают собственные положения при помощи математики, то математические концепции доказываются или опровергаются только средствами самой математики. Нет ничего более фундаментального, чем математика, нет ничего вне математики, нет системы, большей, чем сама математика. Другие науки опираются на математику, математика опирается на саму себя и замыкается на себе же.
8) Мир без математики непредставим. Вы не можете даже вообразить себе Вселенную, в которой нет никакой математики, её пропорций, правил и законов, нет логики. Любая даже самая сумасшедшая фантазия незримо предполагает наличие ну хоть какой-то логики (читай - математики), определяющей облик этого фантазийного мира.
Математика - это просто более глубокий слой реальности, к осмыслению которого мы постепенно подходим. Мы привыкли мыслить в категориях времени, пространства, размера, осязаемой вещественности, но уже Квантовая механика показала нам, что мир гораздо сложнее, чем кажется, и те же элементарные частицы могут быть нульмерными точками и не иметь никакой протяженности в пространстве, а сами пространство и время, как считает, например физик Нима Аркани-Хамед, и вовсе могут быть не фундаментальными, а производными от чего-то иного структурами.
В течение 20 века ученым пришлось менять парадигму мышления и учиться мыслить квантово-механически. В 21 веке нам предстоит пойти еще дальше и научиться понимать мир онтологично-математически. И действительно всё к этому идет, ведь мы по сути уже живем в цифровом мире, цифровой цивилизации, практически полностью созданной математикой, на базе математики. Кстати, говоря языком математики и Квантовой физики, можно сказать, что квалиа как способ компактно упаковать большие объемы данных есть эрмитов проекционный оператор в гильбертовом пространстве.
На самом деле в этой картине мира нет ничего невероятного или мистического. Всё просто: мы как биологические организмы обусловлены химией, химия - физикой, а физика - математикой. Простая иерархия "уровней бытия".
Так вот. Раз сознание математично, а математика онтологична и фундаментальна, то я делаю простой вывод о том, что и сознание может носить фундаментальный характер. На самом деле между математикой и сознанием очень много общего. И то и то - по сути лишь "формы пустоты". Математики нет в вещественном форме, как и сознания. Математика не материальна, но идеальна, то есть она словно имеет свое бытие лишь в сознании, но при этом ей подчиняется абсолютно вся физическая реальность. Ученые и философы на протяжении многих веков размышляли над тем, что вообще из себя может представлять чистая математика и чем на самом деле является сознание. Так может чистая математика и сознание как таковое - это тождественные явления, это одно и то же: лишь формы пустоты, порождающие по определенным правилам всю остальную реальность?
***
Данную свою концепцию о тождестве онтологичной чистой математики и фундаментального сознания я назвал "панпсихистским математизмом".
Да, всё это звучит контринтуитивно, странно и может даже пугающе, но как же много раз в истории уже бывало так, что реальность оказывалась даже еще удивительнее и неожиданно страннее, чем предполагала казалось бы академическая наука на самом высоком уровне.