Эта игра сильно отличается от рассмотренной ранее дилеммы заключенного. Разберем самое главное отличие.

Лучший выбор для Робинзона Крузо зависит от того, что делает Пятница, и наоборот. Не существует оптимальной стратегии ни для одного из игроков, независимо от действий другого. В отличие от дилеммы заключенных, в этой игре нет доминирующей стратегии. Поэтому каждый игрок должен анализировать возможный выбор другого и с учетом этого искать свою оптимальную стратегию.

Робинзон Крузо размышляет подобным образом: «Если Пятница пойдет туда, где пасутся олени, то я получу большую долю добычи, если пойду туда, с другой стороны, я ничего не получу, если пойду на пастбище буйволов. Если Пятница отправится на землю бизонов, должно быть наоборот. Вместо того, чтобы пойти на риск и отправиться в одну из этих областей и обнаружить, что Пятница ушёл в другую, не лучше ли мне самому пойти и поохотиться на зайчиков, как я делал всегда, даже если это приносит мне меньше мяса? Другими словами, не должен ли я взять единицу лута наверняка, вместо того, чтобы рисковать получить три единицы или ничего? Это зависит от того, что, по моему мнению, собирается сделать Пятница, поэтому я должен поставить себя на его место и подумать о том, что он думает. Но он также задается вопросом, что я собираюсь делать, и пытается поставить себя на мое место! » Есть ли конец этим повторяющимся размышлениям о размышлениях?

изменить  четное число камешков на  нечетное, но тут же спохватится, что это слишком просто, и оставит их количество прежним. Поэтому я скажу  «чет!». ». Он говорит  «чет!»  и  выигрывает.  Вот ход  логических  рассуждений маленького мальчика,  которого его товарищи окрестили «счастливчиком». Но,  в  сущности говоря, что это такое?

– Всего  только, – ответил  я,  – уменье  полностью  отождествить  свой интеллект с интеллектом противника.

–  Вот именно, – сказал Дюпен.  –  А  когда я спросил у мальчика, каким способом он  достигает  столь  полного  отождествления, обеспечивающего  ему постоянный успех, он  ответил  следующее: «Когда  я  хочу  узнать, насколько умен,  или глуп,  или добр, или  зол  вот этот  мальчик иди о  чем он сейчас думает,  я стараюсь придать своему лицу точно  такое  же  выражение, которое вижу на  его  лице,  а потом жду,  чтобы узнать,  какие  мысли  или  чувства возникнут у меня в  соответствии  с этим выражением

Потому мальчик из данного рассказа настолько успешен, что он всегда может продумать цепочку «Он думает, что я думаю, что он думает, что....»  ровно на один шаг дальше, чем соперник.

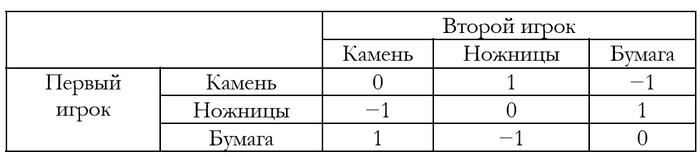
Точно так же и в «камень-ножницы-бумага» нет равновесия Нэша: во всех этих вероятных исходах нет варианта, при котором оба участника были бы довольны своим выбором. Однако чемпионат мира и Всемирное общество ножниц-камень-бумаги (World Rock Paper Scissors Society) собирают игровую статистику. Очевидно, что в этой игре можно повысить свои шансы на победу, зная кое-что об обычном поведении людей.

По данным World RPS Society, камень — самый популярный бросок (37,8%). Бумагой играют 32,6%, ножницами — 29,6%. Итак, теперь вы знаете, что вам нужно выбрать «бумажный» ход. Однако, если вы играете с кем-то, кто тоже это знает, больше не берите бумагу, потому что это ожидаемо. Известен случай: в 2005 году два аукционных дома Sotheby's и Christie's соревновались за право выставить на торги очень крупный лот, в частности, коллекцию Пикассо и Ван Гога по стартовой цене в 20 миллионов долларов. Хозяин пригласил представителей двух домов поиграть в «камень-ножницы-бумагу». Sotheby's без колебаний выбрал бумагу. Победил дом Christie's. На самом деле его представители обратились к эксперту, 11-летней дочери одного из топ-менеджеров. Она сказала: «Камень кажется самым прочным, поэтому большинству людей хочется выбрать его. Но если мы не будем играть с совсем тупым новичком, то он не выберет камень, но будет ждать этого от нас, поэтому, он выберет бумагу. Мы подумаем на один шаг вперёд и выберем ножницы.»

Ящерица? Спок!

Новый вариант игры «камень-ножницы-бумага» популяризировал американский сериал «Теория большого взрыва», изначально созданный Сэмом Кассом и Карен Брайла. Это камень-ножницы-бумага-ящерица-Спок. Здесь действуют классические правила, к которым нужно добавить ящерицу, которая ест бумагу, отравляет Спока, раздавливается камнем и обезглавливается ножницами. Тем временем Спок испаряет камень, ломает ножницы и дискредитирует себя бумагой. Этот вариант, который увеличивает количество комбинаций с 3 до 10, должен уменьшить количество ничей между двумя игроками, которые знают друг друга.

Согласно теории вероятностей, в классическом варианте вероятность выигрыша, проигрыша и повторной игры одинакова и равна 1/3. В улучшенной версии ситуация меняется: вероятность выигрыша и проигрыша составляет по 0,4, а вероятность повторной игры — 0,2. Другими словами, если вы используете улучшенную версию инструмента разрешения споров, то в среднем количество неудачных раундов будет меньше. Тем не менее, между персонажами сериала этот вариант систематически приводит к ничье Спок vs. Спок.

Другой вариант, на этот раз французский, был популяризирован игрой Le Tout (изобретенной Tobiffleurs). Это камень-ножницы-бумага-галактика-клещ. Здесь мы используем классические правила, добавляя галактику, которая дематериализует камень, лист и ножницы, но которая взрывается из-за клеща. Последний может же быть убит камнем, листом или ножницами.

Давайте сравним этот режим игры с другими типами. Вариант «камень-ножницы-бумага-колодец» менее сложен, чем вариант «камень-ножницы-бумага-ящерица-Спок». Есть 4 знака для увеличения количества комбинаций. Это вариант, встречающийся во франкоязычных странах (Франция, Швейцария, Канада) и Германии.

Подробно о дополнительных условиях победы:

• Ножницы падают в колодец,

• Камень падает в колодец,

• Бумага закрывает колодец.

В обычной игре каждый вариант не лучше и не хуже другого. В игре с колодцем, он, конечно же, лучше камня, так он, как и камень, проигрывает бумаге и выигрывает у ножниц, но при их встрече преимущество за колодцем. Таким образом, игрок не заинтересован в использовании камня, потому что, если он вместо этого покажет колодец, его шансы победить любого противника выше. Это означает, что ни один из игроков никогда не будет использовать камень и в игре снова есть три варианта с классическим балансом: колодец, ножницы, бумага. На языке теории игр можно сказать, что колодец доминирует над камнем.

В некоторых местностях и сообществах используются варианты до 9 различных фигур. В шутку на форумах и сайтах также обсуждались варианты до 101 фигуры. Неплохая тренировка памяти и гибкости пальцев, не правда ли?

Построим платёжную матрицу для данной игры. Это игра с нулевой суммой, в которой «1» – это победа, «-1» – поражение, «0» – ничья.

Пусть первый игрок выбирает камень с вероятностью x, ножницы с вероятностью y и бумагу с вероятностью 1−x−y.

Тогда математическое ожидание выигрыша второго игрока в случае выбора им камня будет равно 0∙x+(-1)∙y+1∙(1-x-y).

В случае выбора ножниц это математическое ожидание будет равно

1∙x+0∙y+(-1)∙(1-x-y), а в случае выбора бумаги будет равно  (-1)∙x+1∙y+0∙(1-x-y).

Тогда равенство потенциальных доходов можно записать в виде:

0∙x+(-1)∙y+1∙(1-x-y)=1∙x+0∙y+(-1)∙(1-x-y)= (-1)∙x+1∙y+0∙(1-x-y).

Решив систему двух уравнений с двумя неизвестными, находим, что в равновесии наш ожидаемый выигрыш будет равен 0 и достигается, когда y = x =  1/3.

Аналогично можно определить и оптимальную стратегию для второго игрока. Логично, что в этой симметричной игре она такая же, как и у первого игрока.

На самом деле, «игра в монетку» и игра в «камень-ножницы-бумагу» весьма специфичны. Лучшей стратегией, как мы уже поняли, является случайный равновероятный выбор одного из вариантов. Но тогда средним выигрышем будет 0!.. Как же тогда существуют чемпионы по данным играм? Это просто лотерея или что-то большее? Почему они так популярны? На самом деле, данные игры весьма психологичны, так как, что ни говори, всё равно оба игрока будут пытаться предсказать ход противника.

Самая крупная сумма, выигранная в этих играх, составляет 50 тысяч долларов. Его выиграл в Лас-Вегасе Шон Сирс, который не собирался участвовать в тот вечер в игре «камень-ножницы-бумага». Но он неожиданно обыграл за вечер 300 противников и заслужил прозвище «сумасшедшие пальцы». Сирс объяснял свой успех умением наблюдать за противником в конкретной ситуации и не придерживаться одной тактики.

Мы к проекту относимся очень положительно и часто отправляем туда интересующихся. Как раз таки археологией.

И вот, смотрю я выступление. Да, у меня есть некоторые возмущения по поводу метода изложения, откровенных оскорблений оппонентов и перескакивания с вопроса на вопрос (. Да, у меня есть некоторые возражения по приведенным примерам:

Апполон из Пьомбино (16:22) не тянет на подделку. Это серийная стилизация. Мы не знаем, говорил ли хозяин всем, что это реальная древность. А если говорить об археологии - то никакой фальсификации небыло, было уточнение.

Второй пример вообще ни в какие ворота - Кардиффский великан (17:40). Там археологи вообще не участвовали! Это было с начала до конца шоу. При чем тут археологи?

там еще про хрустальный череп будет, но после того, как этим черепом пытались разыграть Дробышевского, я даже слушать не хочу.

"Томография покажет, что у этой мумии три бедренных кости. Три бедренных кости не бывает в человеке!" (8:30). Уважаемый Александр, бывает три и даже четыре бедренных кости. Сиамские близнецы это называется. И да, в том числе, они бывают в мумифицированном состоянии, потому как диковинка и надоть сохранить. А тут категоричное заявление...

И вишенка на торт. Вот на этом у меня стул обуглился. Александр на полном серьезе рассказал, что чтобы сделать поддельные золотые украшения некие злоумышленники брали "старое" золото и делали из него какие-то изделия.

9:06 - понеслись.

Радиоуглеродный анализ датирует не изделие, он датирует материал.

и понеслось - пример с деревом, пример с "тряпочками" из пустыни Наска иииииии....

"Давайте соберем золотые изделия (9:43) переплавим, отольем из них корону и продадим подороже. Экспертиза покажет древний материал"

Золото. Радиоуглерод. Древний материал. ШТАААА??? То есть, у уважаемого Александра есть какой-то способ датировать золото, причем, после переплавки? А мы-то тут на раскопе сидим и не знаем, контекст фиксируем. Ну не может же быть, чтоб вроде как серьезный популяризатор отсебятину выдавал? Пошла я к специалистам Эрмитажа. Которые как раз занимаются работой с находками из драгметаллов. Спросила - мол, может, и вправду что-то мимо меня прошло? Но и они не знают метода датировать золото вне контекста, ни радиоуглеродом, ни каким другим. Допускаю, что это какая-то совсем новая технология, о которой практики еще не в курсе (тогда заслуживает отдельного ролика!). Но тогда и те, кто делают подделки, не стали бы так морочиться, верно?

@Antropogenez, как так то? Ну взяли же на себя нелегкий труд популяризации и просвещения.

Анализируя результаты турнира, Аксельрод выделил несколько условий, способствующих высоким результатам в игре.

1. Стратегия не должна предавать до тех пор, пока ее не предаст противник. Почти каждая стратегия в верхней части турнирной таблицы обладала данным свойством, назовем его добротой. Интересно, что для получения наибольшей выгоды для себя, то есть из чисто корыстных побуждений, стратегия не должна предавать противника первой.

2. Стратегия должна реагировать на попытку противника предать ее. Стратегия всепрощения обречена на провал, потому что всегда найдется «подлая» стратегия, которая непременно воспользуется такой наивностью. Другими словами, успешная стратегия должна быть мстительной.

3. Если противник перестанет предавать, хорошей стратегией будет возобновление сотрудничества. Стратегия должна быть мягкой. Стратегия должна уметь прощать.

4. Зависть – желание набрать очков больше, чем соперник. Это – плохое свойство, хорошие стратегии независтливы.

Вывод из этого эксперимента звучит странно: для того, чтобы стратегии-эгоисты получали как можно больше выгоды для себя, они должны быть добрыми, независтливыми и прощающими. Неожиданно, не так ли?

Игра в монетки

Давайте проанализируем следующую игру.

Имеется два игрока. Один из них прячет монету в руке. Другой пытается угадать, где монета. Игрок, угадавший, в какой руке монета у партнёра, забирает её. Если угадать не получилось, мы отдаём партнёру по игре свою монетку.

Построим матрицу платежей для данной игры.

Как мы видим, в данной игре ВООБЩЕ нет никаких равновесий – ни по Нэшу, ни Парето-оптимальных.

Как вы думаете, какое будет равновесие в смешанных стратегиях в данной игре?

Вы можете попробовать поиграть в данную игру со своими друзьями, чтобы попробовать найти вашу лучшую стратегию.

Можно короче: принцип ведомого (отзеркаливание действий соперника).

Но у этой модели проблема в том что ты ведомый, т.е. реагируешь на ситуацию, а не задаёшь её исход.

2) «... Для однократной игры партнёрам стоит использовать принцип минимакса вне зависимости от того, содержит ли матрица платежей седловую точку или не содержит. Этот же принцип целесообразно использовать и при многократной игре с седловой точкой. ...»

---

Тут проблема в том что игрокам не всегда понятно когда игра разовая.

Вроде отжал «здесь и сейчас» по максимуму свою «львиную долю» пользуясь «правом силы», а игра оказалась в долгую (многократные игры).

И тут в игру вступает новая переменная «память о прошлых играх» (результаты предыдущих взаимодействий).

И оказывается что «никто не забыт, ничто не забыто» и тебе могут выставить «счёт» за прошлое. Аналогично и ты можешь «предъявить» «ты мне - я тебе». По сути с этого момента некооперативная игра начинает приобретать черты кооперативной, т.к. приходится учитывать интересы другого игрока, а не тупо «урвал побольше - убежал подальше», т.к. «куда ты денешься с подводной лодки?»© (мы в этой лодке до конца игры).

В пример см. Процессный подход и совершенствование с пункта «В».

3) «... Поэтому «чем случайнее, тем вернее», именно непредсказуемо случайное чередование стратегий не позволит добиться сопернику выигрыша. ...»

---

В реальности тут скорее начинается «картельный сговор». Игра из однократной превратилась а серию/цикл и чтоб её не порушить своей, или чужой жадностью и безрассудством приходится договариваться о внутренних правилах этой серии игр.

Вилке выигрышев в среднем и максимально для каждого в отдельно взятой игре (самоконтроль), допустимом давлении на оппонента и пр.

Но опять-таки это всё для формально равноправных участников. Если один из игроков (например фирма) думает что «я здесь власть) и купив трудовые услуги человека может его эксплуатировать. ... В реальности в договременоом сотрудничестве человек пользуясь «информационной асимметрией» https://ru.m.wikipedia.org/wiki/Асимметричность_информации (неявным знанием о работе для которой его наняли https://ru.m.wikipedia.org/wiki/Неявное_знание) будет восстанавливать социальную справедливость в меру своего понимания. В основе этой философии поведения лежит https://ru.m.wikipedia.org/wiki/Занавес_неведения и Некооперативные игры. Размышляя над «Ультиматумом» (мой комментарий по поводу игры «Ультиматум»).

4) Как писал чуть ранее неоднократность игры, её переход в серию + память о прошлых играх переводят эту «сериальную игру» в категорию кооперативных, в ином случае исходя из высших побуждений (справедливость) вечно проигрывающий игрок может из неё выйти и тем самым уничтожить оставив всех без выигрыша (см. игра «Ультиматум»).

Ага, я сейчас опять и снова про инновационную сферу и рационализаторскую деятельность.

Фирма считающая себя монополистом на местечковом рынке инноваций демпенгует через закупочные цены и роялти (авторские отчисления) на рацпредложения, изобретения, оптимизации и прочие инновации исходя из логики: «кому ты ткт ещё сможешь продать свои рацухи?, бери сколько заплатили».

Тем более что чиновники принимающие решения считают себя анонимным, организованным единством (говорящим от лица компании), а всех этих «Кулибиных» оголодавшими (финансирование из других источников) которые не умеют думать наперёд (просчитывая свою выгоду), которые не могут посмотреть историю прошлых игр для ретроспективного и проективного анализа инновационной игры чтоб понять какова будет их «гонорар успеха», или просто общаясь в своей среде поспрашивать у тех кто сыграл и сделал выводы уже Делёжка шкуры не убитого медведя (см. комментарии).

Как успехи?

См. https://ru.m.wikipedia.org/wiki/Индекс_глобальной_конкурентоспособности + https://ru.m.wikipedia.org/wiki/Интеллектуальный_капитал. В общем плохо, пока у нас игры «Царь Горы» и попытка урвать сиюминутно в псевдоразовой (однократной) игре, считая что тут игра с нулевой суммой, и готовые загрысть ради «победы». В других местах приоритет отдают долговременному, взаимовыгодному сотрудничеству (кооперативные игры) т.к. понимают что автор «гонорар успеха» потратит на себя в месте обитания, т.е. оставит деньги «на земле» и в экономике, а не законсервирует в золотом унитазе, часах стоимостью в элитную квартиру, океанскую яхту на которой бываешь 1~3 недели в год и прочий «дорого, пафосно и бесполезно».

Классическая https://ru.m.wikipedia.org/wiki/Игра_РП-РџР% где каждый сам за себя и сам по себе что и приводит к https://ru.m.wikipedia.org/wiki/Трагедия_антиобщин в виде проигрыша всех кто в этой «лодке». Ага, оказывается мы все по одну сторону, только на разных уровнях общества и государства, кто-то «как рабы на галерах», кто-то рулевой, кто-то просто разносчик чего-то там и вместо слаженной работы (кооперации) выясняем кто главный, кто-то себе строит плот из обшивки корабля (мне нужнее), кто-то топливо продаёт чтоб купить себе велосипед/трактор, кто-то паруса порезал на воздушный шар. В сумасшедшем доме попытка одиночного побега :-))) В общем, самовыживание без сотрудничества в основе которой «верхи не могут, низы не хотят» что и приводит к внутрикорпоративным войнам на истощение (в живых должен остаться только один).

По некоторым позициям обогнав нас в «эволюционной гонке» прогресса (НТР) на десятилетия (та же микроэлектроника, биоинженерия и пр. промышленное (а не лабораторное) производство).

«Гонка на дно» продолжается.

Всё становится сложнее, когда игрок «я такой внезапный» наталкивается на двухшляпного. В первый день он сделает одну шляпу, а во второй – две. Но далее каждый игрок будет делать по 2 шляпы каждый день. Тогда каждый получит средний выигрыш в 11 евро, так как выигрыш в первый день не имеет значения при вычислении средних над бесконечным периодом.

Согласовав полученные значения, мы переходим к матрице выигрышей, указанной на таблице. Данная таблица  – лишь малая часть общей платёжной матрицы повторяющейся дилеммы заключенных, потому что мы рассмотрели только три стратегии из счётного множества. В полной таблице мы сможем наблюдать бесконечное множество равновесий, так какое же необходимо выбрать? Или к какому сойдётся игра? На самом деле, ответ на данный вопрос получить так просто нельзя, поэтому обычно в задачах просят просто найти множество равновесий по Нэшу, или Парето-оптимум, или, опять же, ставят более явный вопрос.

Смешаные стратегии

Если матрица платежей содержит седловую точку, то существуют хорошие стратегии для обоих игроков. Для однократной игры партнёрам стоит использовать принцип минимакса вне зависимости от того, содержит ли матрица платежей седловую точку или не содержит. Этот же принцип целесообразно использовать и при многократной игре с седловой точкой.

Стратегия меняется, как только речь заходит о многократной игре без седловой точки. В этом случае постоянное повторение стратегии может привести к невыгодным результатам. Например, если мы будем играть в «камень-ножницы-бумагу» и ходить всё время только одинаково, то даже если соперник немного умственно неполноценен, успеха нам это не принесёт.

В повторяющихся играх каждая из стратегий однократной игры называется чистой стратегией.

Смешанная стратегия – это присвоение вероятности каждой чистой стратегии.

Это позволяет игроку случайным образом выбирать чистую стратегию. Поскольку вероятности непрерывны, игроку доступно бесконечно много смешанных стратегий. Интерес к смешанным стратегиям объясняется просто – если соперник определит, какая из ваших стратегий будет применяться в очередной игре, он сможет использовать эти знания для улучшения своего результата (и ухудшения вашего). Поэтому «чем случайнее, тем вернее», именно непредсказуемо случайное чередование стратегий не позволит добиться сопернику выигрыша.

Логично, что  чистые стратегии можно представить как частный случай смешанных, например, в том случае, когда частота одной из стратегий – 1, а остальных – 0.

В оптимальных смешанных стратегиях игрок, отклонившийся от своей оптимальной стратегии, изменяет средний выигрыш в невыгодную для него сторону.

Полностью смешанная стратегия – это смешанная стратегия, в которой игрок присваивает каждой чистой стратегии строго положительную вероятность.

Решение игры есть совокупность применения каждым из игроков своих оптимальных стратегий.

Цена игры – результат, достигнутый при решении игры, то есть, средний выигрыш (математическое ожидание выигрыша) при применении оптимальных стратегий обоими игроками.

Те стратегии, которые присутствуют в оптимальной стратегии игрока с ненулевыми частотами, называются полезными (другое название – активными).

В 1928 году фон Нейман доказал, что для каждой игры имеется не менее одного решения. Это решение может находится в том числе в области смешанных стратегий.