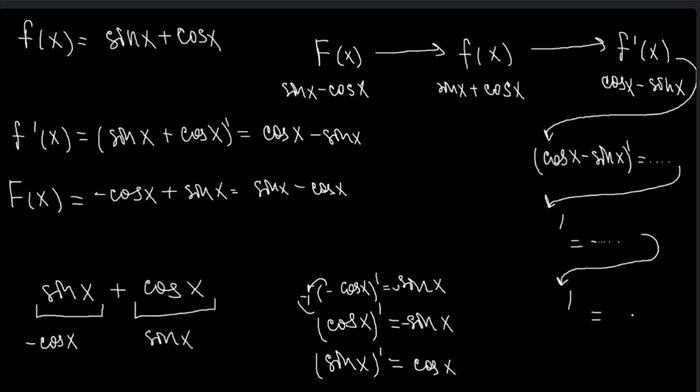Чем занимаются историки математики и в чём заключается феномен Ростовской научной историко-математической школы? В лекции будет рассказано о предпосылках формирования в Ростове-на-Дону исследований историко-математической тематики, о наиболее крупных ростовских математиках, работавших в этой области, и их достижениях, о современном состоянии и перспективах историко-математических исследований в ЮФУ.

Рассказывает Вячеслав Пырков, кандидат педагогических наук, доцент кафедры теории и методики математического образования Института математики, механики и компьютерных наук им. И.И. Воровича ЮФУ.

Наше множество — это жирные красные точки (n, √2n), n∈ℕ₀. И нам нужно доказать такое: если их все заэквивалентить в один квадрат 2π×2π, получим плотное множество. А для этого действуем так.

Ткнём где-то точку (x,y), выберем маленькое ε, и докажем две вещи.

АДЫН. Можно найти точку, достаточно близкую (по эквивалентности) к любому x (на y чхаем).

2πn+x заменим на (2π−6)n+x, ничего не изменится. Обозначим 2π−6≈0,28 за a.

Начнём с x=0 и сделаем несколько шажков этой формулой: на третьем не добираемся до единицы на 0,15, а на четвёртом уже имеем 1,13. Таким образом, мы шажками на a (что эквивалентно шажкам на 2π) можем приблизиться к целому числу не просто на a≈0,28, а на a/2≈0,14 — не только для x=0, а для любого x.

Обозначим эти четыре шага как «шаг второго порядка», и он короче, чем a/2. Шаг третьего порядка, состоящий из семи шагов второго порядка, будет ходить на 0,0088 уже в минус, и так далее — то есть мы можем соорудить шаг короче любого ε.

Что может пойти не так? Только то, что какой-то шаг станет нулём — но это возможно, если изначальный шаг 2π рациональный. То есть мы полагаемся на несоразмерность шагов по разным координатам.

Кроме того, отсюда видно: чтобы добиться точности ε, нужно быстро растущее при ε→0, но всё-таки зависящее только от а и ε (но не от начального x!) количество элементарных шагов s(a,ε). Функция, как уже сказано, определена только для рациональных a, но она симметрична по a, убывает для отрицательных a и возрастает для положительных, и ничего не стоит её доопределить. Чему равна — облом выписывать: скажем, для a≈0,4 и ε=0,05 она s(0,4; 0,1) = 3 + 6·3 + 11·6·3 (ходьба шажками 0,4, затем чуть меньшими 0,2, затем чуть меньшими 0,1).

Поскольку a лежит в пределах ±0,5, и чем оно больше по модулю, тем выше наше потребное количество элементарных шагов s, то у функции есть верхняя грань по a — s(ε) := maxₐ s(a,ε) = s(±0,5, ε).

ДЖВА. Можно найти точку, достаточно близкую к любому x и y.

По первому утверждению приближаемся к нашему x с точностью ε/2. При этом y выходит произвольный.

Опять-таки по первому утверждению добиваемся шажка по x не более ε/2s(ε). Приняв то, что получилось, за базовый шаг, приближаемся к нашему игреку с точностью ε, при этом по x уйдём максимум ещё на ε/2.

Так, речь в байке о Тамме и махновце шла о ряде Маклорена, то есть простом частном случае ряда Тейлора. Тейлор опубликовал свою работу в 1715, и он был не первым, кто пользовался этим рядом. Ряд Тейлора в целом и Маклорена в частности был обоснован еще Ньютоном в неопубликованных работах 1690 годов, а пользовались такими рядами Ньютон, Коллинз, Грегори еще около 1670. Опубликован же подробный анализ рядов Маклорена был самим Маклореном в 1740-х.

Остаточные члены в форме Лагранжа и Коши появились заметно позже: в 1797 и 1823, соответственно. Общей вид дифференциальной формы придуман не то Рошем в 1858, не то Шлемильхом примерно тогда же. Интегральный вид придуман еще Коши в 1821. Остаточный член в форме Пеано появился в 1910-х годах благодаря недавно придуманной нотации о-малого (Э. Ландау, 1909).

Форма Пеано не позволяет сделать численную оценку остаточного члена, так что Тамму из байки про махновца она бы не пригодилась. Для оценки достаточно дифференциальной формы Лагранжа, опубликованной за век до рождения Тамма.

Проходили ли всё это в дореволюционной России? В школах - нет. В 7 классе реальных училищ проходили матан, но так же поверхностно и на пальцах, как сейчас - в 10-11 классах. Киселёв, написавший учебник "Начала дифференциального и интегрального исчислений" в 1908 году, придумал своё, довольно странное и нестрогое основание матанализа. Ряда Тейлора там нет, материал в целом похож на современный для непрофильных классов, типа того, что в учебнике Колмогорова.

Тамм ходил не в реальное училище, а в гимназию, но сомневаюсь, что в гимназиях преподавали намного больше математики.

Другое дело - университеты. Курсы матанализа для студентов появились в России еще в XVIII веке. Так, уже в 1796 году Гиларовский издал учебник "Сокращение вышней математики" для учительских гимназий/семинарий. Не знаю, были ли там ряды Тейлора-Маклорена.

Почти уверен, что остаточный член был в учебнике Зернова (1842): в доступных мне сканах отсутствуют нужные страницы, так что могу лишь утверждать, что сами ряды Тейлора и Маклорена в Зернове точно были, насчет остаточного члена не гарантирую.

И совершенно точно остаточный член в форме Коши был в "Курсе анализа" Хандрикова (1887), причем почти в современной нам нотации:

В целом же в школьной и вузовской программе первых пары курсов по математике нет почти ничего, а по физике - не так много фактов и методов, неизвестных в XIX веке.