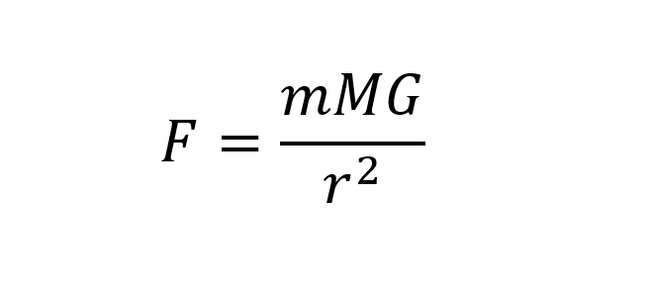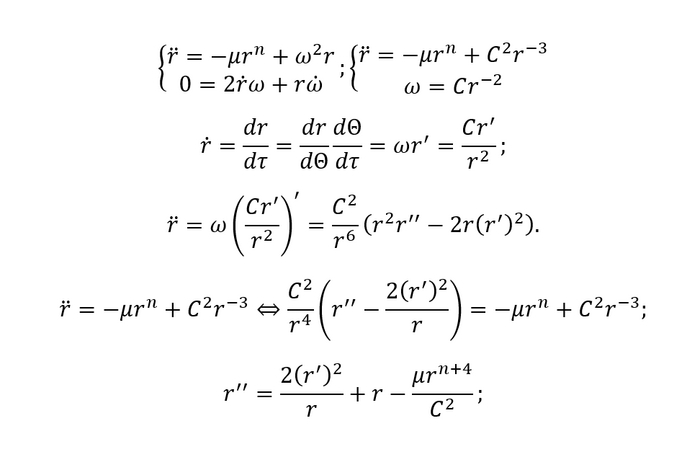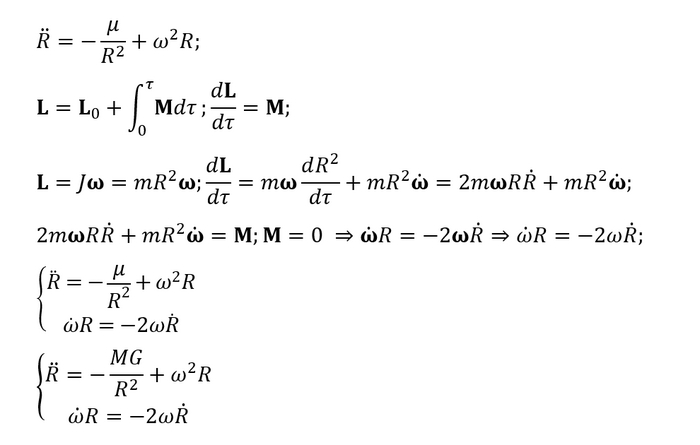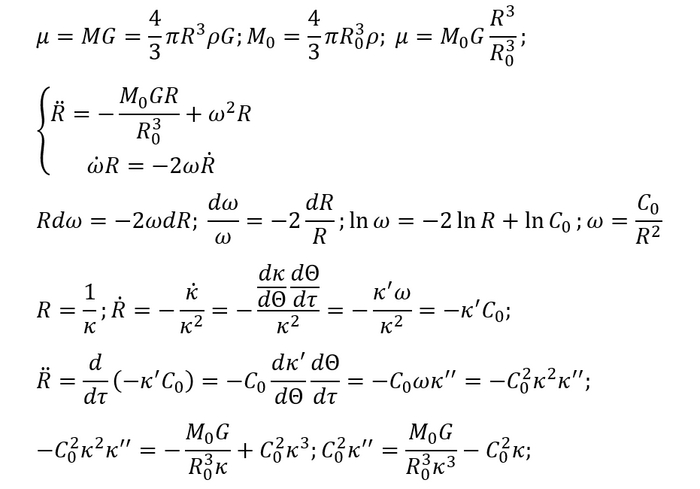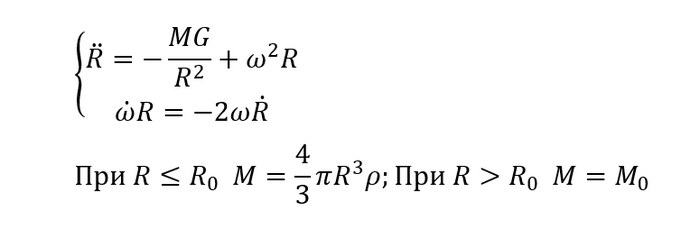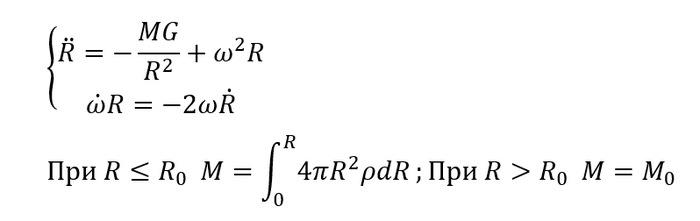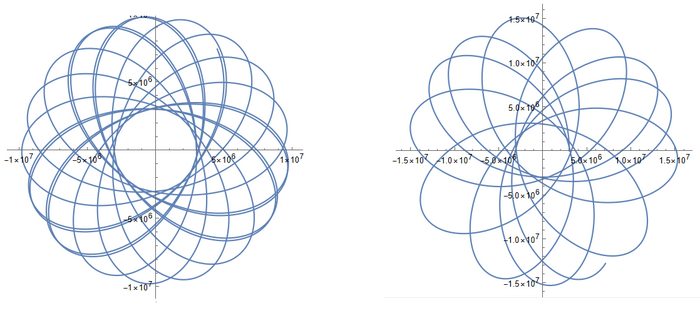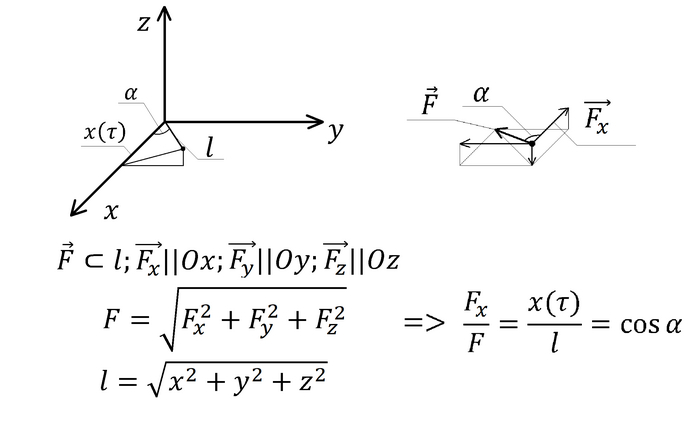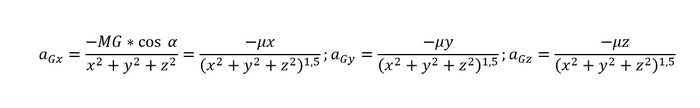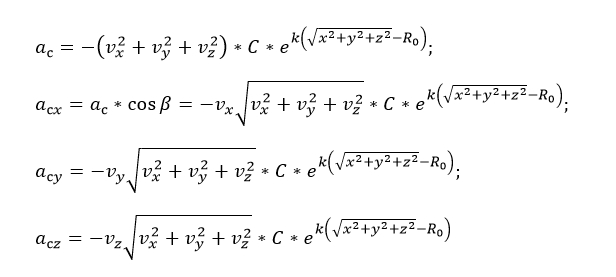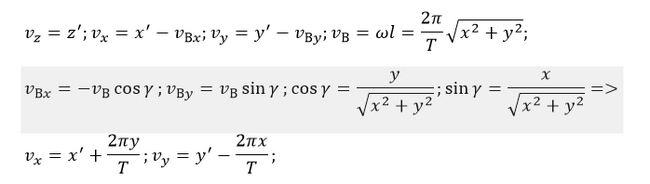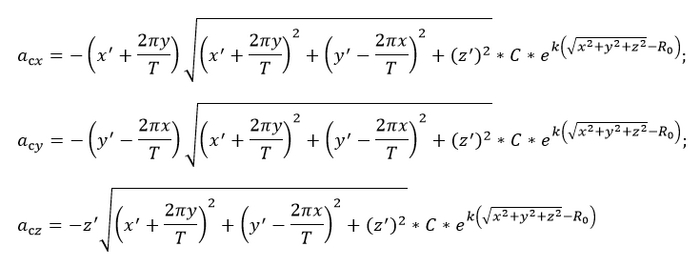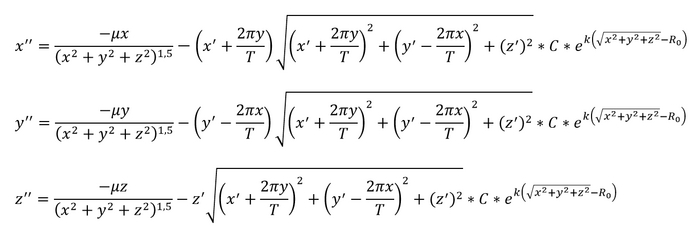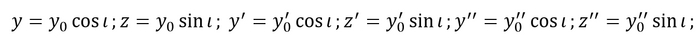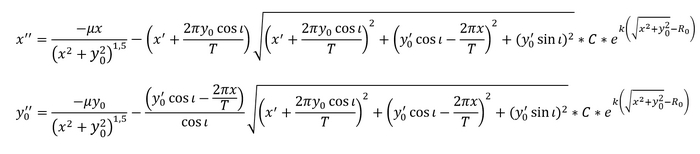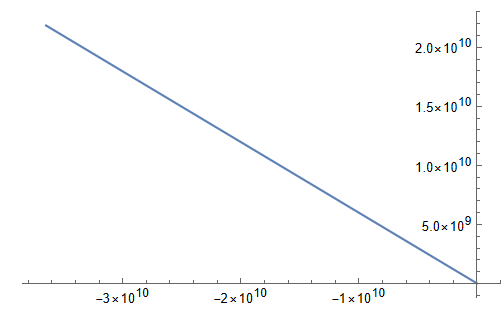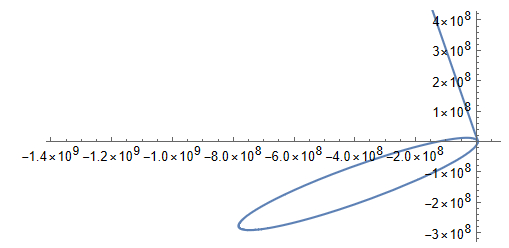Всем доброго времени суток. Чуть менее года назад мне попался пост про SpinLaunch, где в комментариях речь зашла о том, можно ли выйти на орбиту при помощи пушки и без включения двигателей. Ну и мне захотелось узнать ответ на этот вопрос. Захотелось, но то времени не было, то просто лень было что-то делать. Но вот руки дошли до поста, поэтому прямо сейчас проверим, можно ли выйти при помощи пушки на орбиту? А также в конце затрону вопрос о том, как лучше всего выходить на орбиту с использованием и пушки, и двигателей
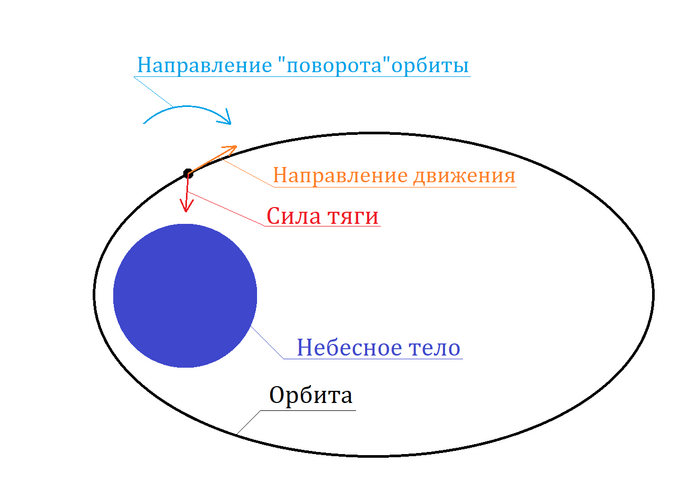
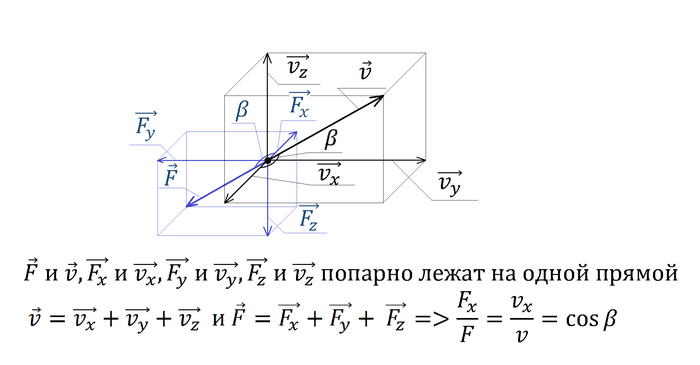
На первый взгляд кажется, что выйти на орбиту, придав спутнику импульс на поверхности планеты, невозможно. Если не учитывать сопротивление воздуха, то точка старта будет принадлежать орбите аппарата, а еще там вертикальная скорость будет положительна, из чего следует, что перицентр окажется ниже поверхности. Но вот если добавить атмосферу, то картина изменится. Спутник всегда будет двигаться только вверх в атмосфере (ему все-таки из нее выбраться надо). Поэтому аэродинамическое сопротивление будет толкать спутник вниз. Если вы знакомы с орбитальной механикой и/или играли в Kerbal Space Program, то, я уверен, знаете, что если включить двигатель по направлению к или от небесного тела, то орбита начнет как бы "поворачиваться" относительно положения аппарата. Более понятно это показано на картинке, где орбита будет отчасти похожа на текущую орбиту нашего спутника в какой-то момент времени при движении в атмосфере:
Можно сразу заметить, что при таком "повороте" орбиты перицентр увеличивается. Значит теоретически может быть такой случай, когда спутник сам выйдет на орбиту. Давайте это проверим и попытаемся найти такой случай
Модель спутника
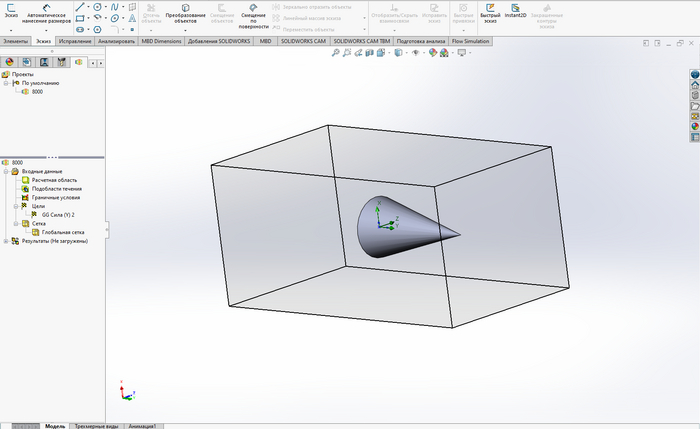
Так как основы никакой нет, то сами выберем, каким будет спутник. В качестве модели я решил взять конус диаметром 1 м, углом раствора 30 градусов и массой 500 кг. Этакий набор кубсатов под бронированным колпаком :)
В полете важную роль будет играть сопротивление воздуха, поэтому вычислим среднее значение коэффициента сопротивления воздуха. Но не совсем того, что нам дает классическая формула F = p * S * c * v^2 / 2, а немного другого. Запишем формулу ускорения от аэродинамического сопротивления: a = p * S * c * v^2 / 2m, заметим, что все, кроме p и v, - это константы. p, то есть плотность среды, мы заменим на p0 * e^(k * H), то есть аппроксимируем плотность от высоты при помощи экспоненты. Перепишем формулу ускорения: a = (p0 * S * c /2m) * v^2 * e^(k * H). Теперь все константы перепишем в одну a = C * v^2 * e^(k * H). Вот эту C мы и найдем
Сама по себе C - это не константа, так как коэффициент сопротивления воздуха для одной и той же формы разный при разных скоростях. Однако на больших скоростях он колеблется незначительно (что мы дальше и увидим), поэтому его можно принять константой (в целом, для более точного решения нужно C найти через интерполяцию его значений при конкретных скоростях, но для этого нужно взять довольно много точек, что делать не особо хочется, да и на точность это сильно не повлияет, зато прибавит лишней работы)
Ну коль надо измерять сопротивление воздуха, то нам понадобится САПР, в моем случае это SolidWorks. Запускаем, создаем модель, заходим во FlowSimulation и создаем проект:
Скорость -30000 м/с - один из расчетных случаев
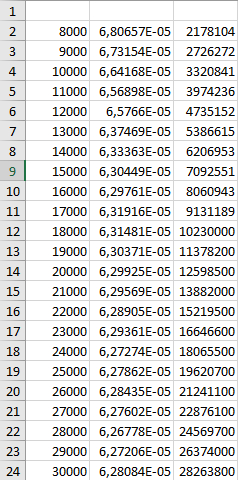
Теперь поставим в проекте цель находить силу по оси Oy и по несколько раз запустим расчет, каждый раз меняя значение скорости потока воздуха. Я буду измерять с 8000 м/с до 30000 м/с с шагом в 1000 м/с. Для каждой скорости записываем действующую силу. Дальше, возвращаясь к формуле ускорения, мы избавимся от e^(k * H). Так как в SolidWorks-е воздух имеет такую же плотность, что и воздух у поверхности Земли при н.у., то переменная H становится равна нулю, а экспонента - единице. Ну а чтобы вычислить тот самый коэффициент, мы будем силу делить на массу и на квадрат скорости (сила на массу даст ускорение, а если ускорение поделить на квадрат скорости, то получим только коэффициент, ну и еще экспоненту, но мы от нее избавились). Короче говоря, пишем таблицу в экселе:
1-ый столбец - скорость, 2-ой - искомый коэффициент, 3-ий - сила, действующая на модель при данной скорости
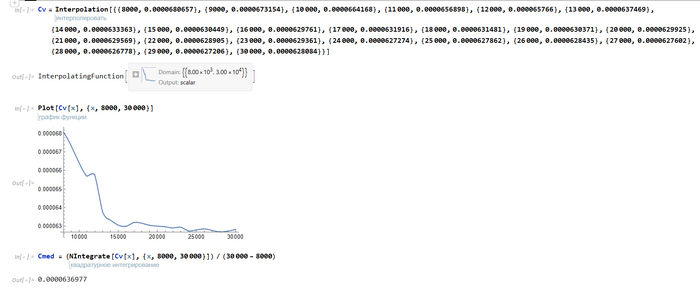
Осталось найти среднее значение. Но как это сделать? Будем действовать так же, как при нахождении средней скорости: проинтегрируем функцию C(v), полученную интерполяцией табличных значений, а затем разделим на разность пределов интегрирования. В качестве пределов интегрирования будут использованы минимальная и максимальная скорость, что логично. Запускаем Wolfram Mathematica, пишем и выполняем следующий код:
Можно заметить, что сам коэффициент колеблется незначительно, что нам на руку
В целом, это все, что нужно знать про модель. В решении мы пренебрежем уменьшением массы от испарения аблятора, напряжения и деформацию рассматривать не будем (так как первое нам не нужно, а второе будет очень маленьким). Также примем, что наш конус при движении острием вперед устойчив, то есть его ось всегда совпадает с вектором скорости воздуха. На деле так случается не всегда, все зависит от центра масс, но будем считать, что спутник мы сделали устойчивым
Плотность атмосферы
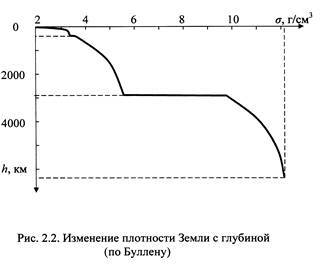
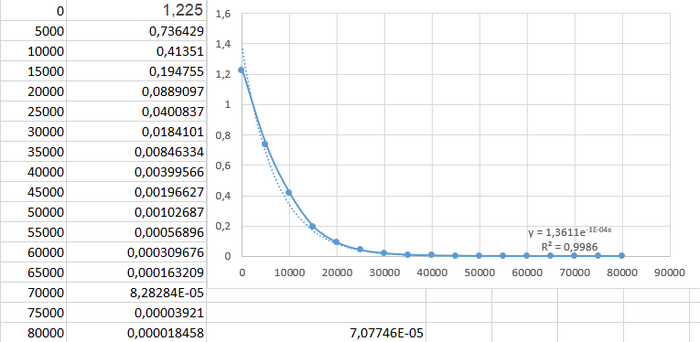
У нас остался неизвестный коэффициент при экспоненте, его тоже надо найти (конечно, можно и плотность интерполировать, но для этого нужно много точек при больших высотах, что, опять же, делать не очень приятно, к тому же приближение через экспоненту работает довольно точно). Находим ГОСТ 4401-81 Атмосфера стандартная и из него берем плотности воздуха при разных высотах, далее записываем их в эксель и строим график. Создаем линию тренда, делаем ее экспоненциальной и выводим уравнение на график
Тут же сразу замечаем, что у полученной функции в нуле плотность не равна плотности воздуха при нулевой высоте. Поэтому полученный прежде коэффициент для сопротивления воздуха нужно переделать. В нем есть начальная плотность, которая как раз равна 1,225 кг/м^3. А при приближении экспонентой она должна быть равна 1,3611 кг/м^3. Поэтому сам коэффициент разделим на 1,225 и домножим на 1,3611. На картинке он есть, вон в низу красуется)
Составление модели полета
Вводные данные есть - значит можем приступать к самой модели полета. Сразу определимся, что в ней будем учитывать, а что не будем. Во-первых, в учет пойдут только сила тяжести и сила сопротивления воздуха. Остальные силы очень малы, поэтому ими можно пренебречь. Помимо этого не будем учитывать моменты. Мы заранее приняли, что аппарат будет устойчив, поэтому можно не записывать уравнения моментов и не вводить зависимость сопротивления воздуха от ориентации: спутник всегда направлен по движению (a.k.a. по програду). Также по мелочи, не будем учитывать изменение радиуса Земли (и эллиптичность самой Земли в сечении) при разной широте старта
Систему координат возьмем декартову, трехмерную. Нуль координат будет совпадать с центром Земли
Приступим к формулам. Нам надо выразить ускорения по 3 осям
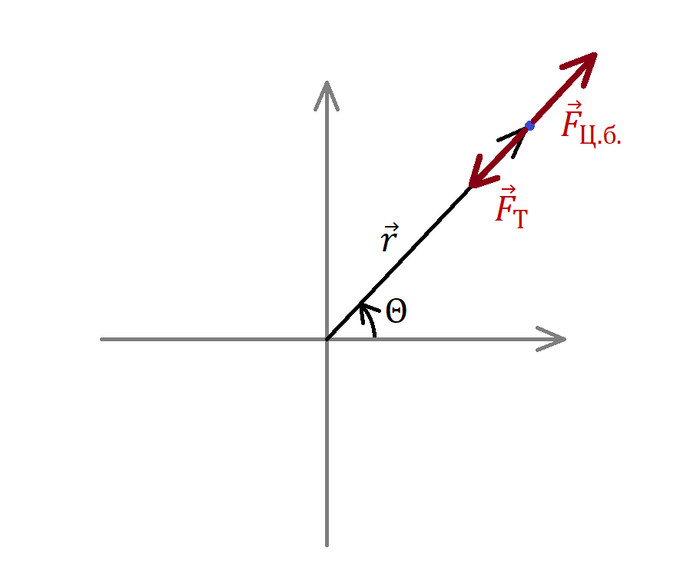
Начнем с силы тяжести. При помощи чертежа находим, как будет зависеть проекция силы на ось от координат тела:
Выражение записано только для оси Ox, однако оно аналогично для и для Oy и Oz
Теперь выражаем F, вернее a, и записываем проекции ускорения от силы тяжести на каждую из осей
Теперь строим чертеж для силы сопротивления воздуха:
И также выражаем ускорение от АС, а затем и ускорение в проекциях
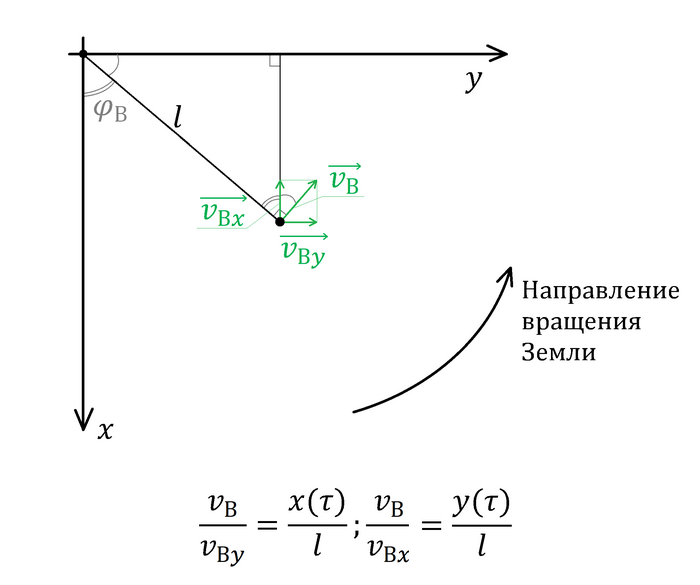
Однако здесь можно сразу заметить один нюанс: мы не все выразили через x, y и z и их производные. Дело в том, что Земля крутится, а вместе с ней и атмосфера. При помощи чертежа определим, как зависит скорость воздуха от координат и перезапишем v-шки через них:
Перезапишем формулы для сопротивления воздуха:
И составим сами уравнения модели:
Казалось бы все, модель готова. Но тут есть нюанс. Работать с трехмерной моделью полета не очень удобно, к тому же это более ресурсозатратно (а еще у меня Wolfram может сильно косячить с графиками в 3D). Поэтому сократим количество измерений до 2
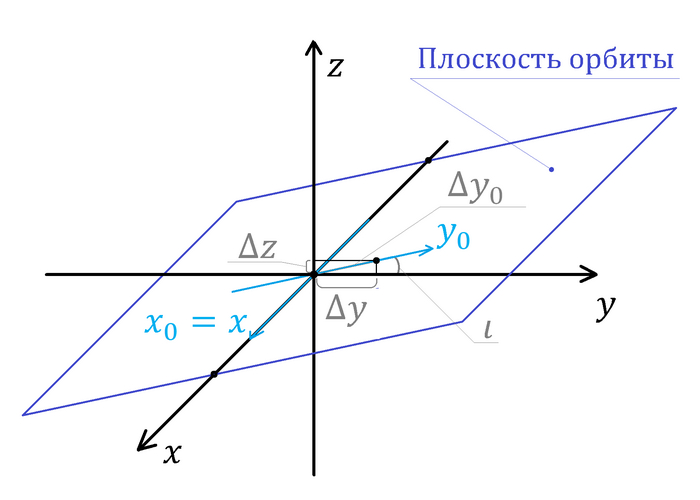
Для этого примем, что орбита находится в одной плоскости (на деле она чуть-чуть смещается, как раз из-за вращения атмосферы, но это смещение довольно мало). Плоскость орбиты должна проходить через место старта и нуль системы координат. Из этого следует, что ее наклон к плоскости Oxy равен широте места старта. Теперь для удобства примем, что ось Ox принадлежит этой плоскости (это соответствует случаю, когда x-координата места старта равна нулю). Теперь на этой плоскости проведем систему координат Ox0y0, причем x0 совпадает с x (поэтому вместо x0 будем писать просто x). Построим чертеж и выразим y и z через y0, а также запишем их производные первого и второго порядка:
Перепишем систему в двух измерениях. y0 выразим из y (выражение через z и y дают разные формулы, которые численно не сильно отличаются. Это как раз из-за того, что на деле орбита не находится в одной плоскости):
Поиск решений для задачи
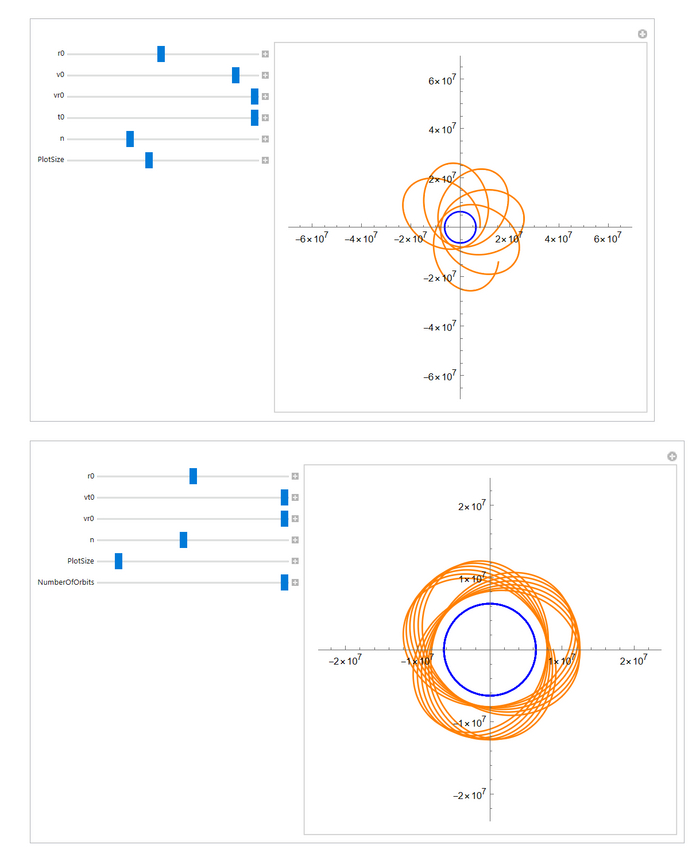
Теперь надо найти такие комбинации начальных скоростей по обеим осям, чтобы аппарат вышел на орбиту (или убедиться, что их нет). Так как данная модель не имеет аналитического решения, то придется просто перебирать решения (сразу добавлю, что для всех параметров сразу все же можно найти решение, для этого нужно решить систему R(t0) = (6371000 + 180000) м) и R'(t0) = 0 (здесь вводится полярная система координат), однако я не нашел способа сделать это в Wolfram-е, а также для такого решения банально не хватает мощностей моего компьютера). Это не даст стопроцентный ответ на поставленный в начале вопрос, но по самим траекториям можно будет предположить, каков ответ
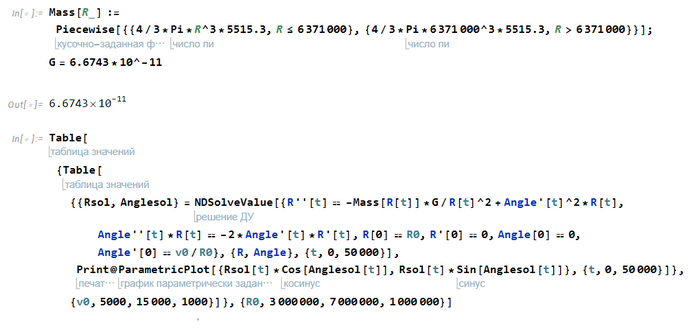
Как будем перебирать? Я решил выбрать более менее подходящий вариант между точностью и затратами на расчет, поэтому выбрал ограничения для начальных горизонтальной и вертикальной скоростей в 3000 м/с и 8000 м/с соответственно снизу и 30000 м/с сверху (да, стоило в начале посчитать коэффициент вплоть до 30000*Sqrt(2) м/с, но коэффициент ведь считаем постоянным, а поэтому можно использовать и тот, что есть). Шаг для обеих скоростей выберу в 500 м/с. В итоге получим 2475 траекторий, которые надо отсмотреть и проанализировать
Также в решении надо будет ввести ограничение по времени внутри системы (то есть от какого до какого момента моделировать полет). Для этого нижнее (оно же начальное) значение времени будет равно 0, а верхнее я решил принять равным орбитальному периоду для спутника на эллиптической орбите с апогеем ровно на границе сферы тяготения и перигеем в 180 км (число взято не совсем из головы, изначально я предполагал вводить уплощенную модель, которая имеет аналитическое решение, чтобы определить, среди каких скоростей искать решение, и вот там как раз спутник должен был выйти на орбиту с перигеем в 180 км. Но решение этой модели давало вообще неправильные цифры (для примера - чтоб хотя бы просто не упасть на Землю, нужна была горизонтальная скорость в ~150 км/с, что в полной модели давало достижение второй космической), поэтому я от него отказался)
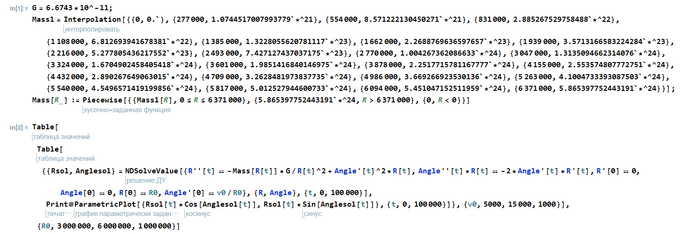
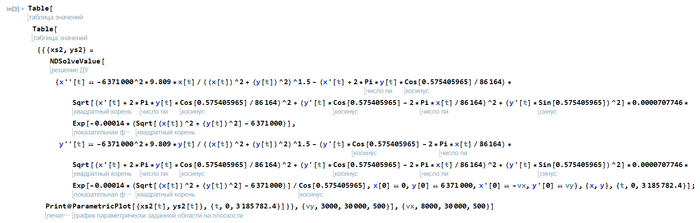
Итак, пишем код, запускаем его и идем пить чай, че еще делать то)
Через несколько минут приходим назад и мотаем вниз в поиске кучи надписей Null в фигурных скобочках. Если они есть и новых графиков не появляется, значит расчет окончен. Можем приступать к анализу
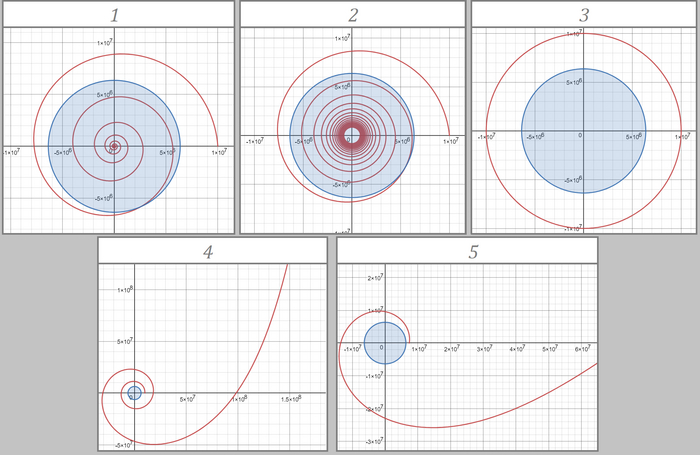
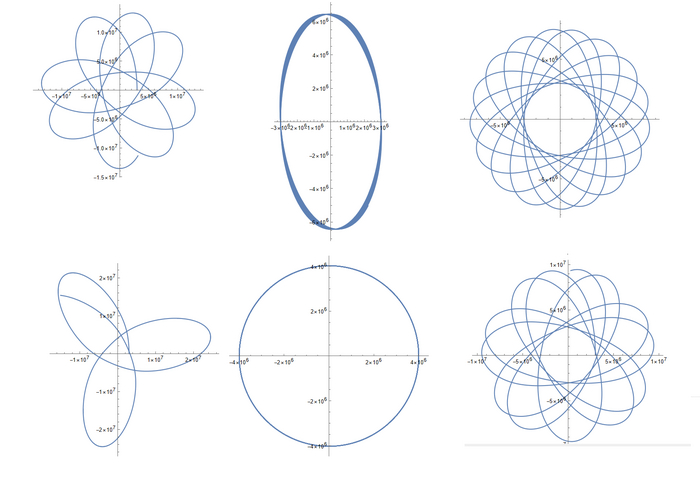
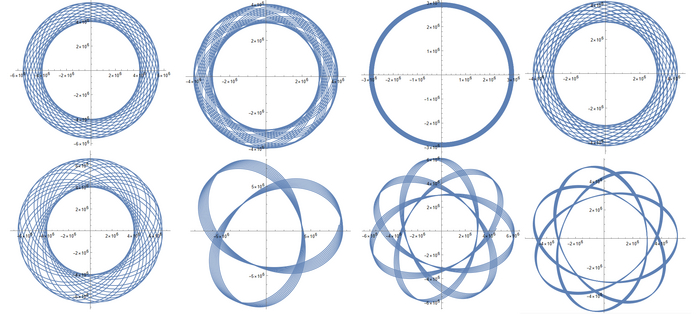
Но перед этим сразу определим, какие графики мы можем теоретически получить. Их 4 типа:
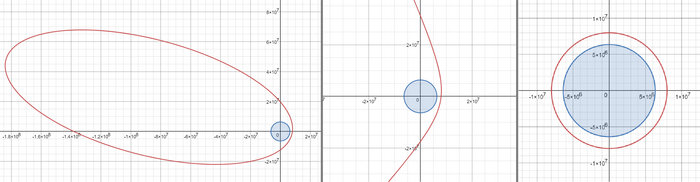
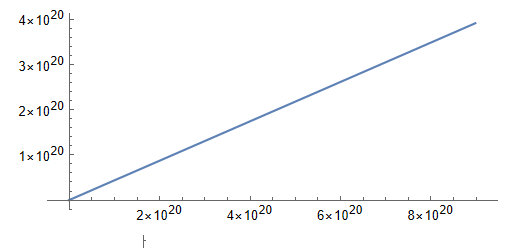
Прямая с малой кривизной. На координатных осях значения до примерно 1*10^11. Это случай, когда аппарат набрал вторую космическую скорость и покинул сферу тяготения Земли
Прямая с малой кривизной. На координатных осях очень большие значения, больше чем в первом типе. Это случай когда спутник упал на Землю. Из-за экспоненциальности плотности воздуха и учета вращения атмосферы спутник, оказавшись под поверхностью планеты, начинает испытывать очень сильное действие силы сопротивления воздуха, которое не останавливает его, а заставляет двигаться. В купе с этим из-за перехода к 2 измерениям спутник не движется по "орбите" под землей, а очень сильно ускоряется крутящейся атмосферой, из-за чего набирает гигантскую скорость и улетает от Земли на миллионы световых лет
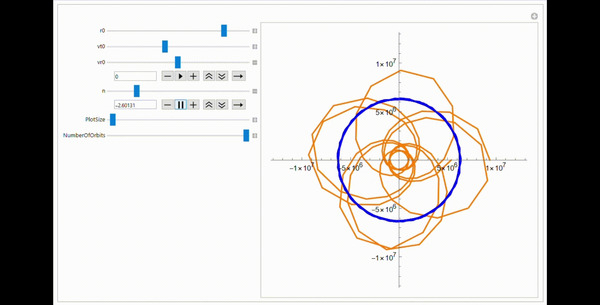
Разомкнутый эллипс. Это тот случай, когда апогей оказался не сильно выше границы сферы тяготения. Так как есть ограничение по времени, заданное максимально высокой орбитой, то при апогее ниже границы, эллипс должен быть замкнутым (или почти замкнутым, но там расстояние между началом и концом кривых должно быть маленьким)
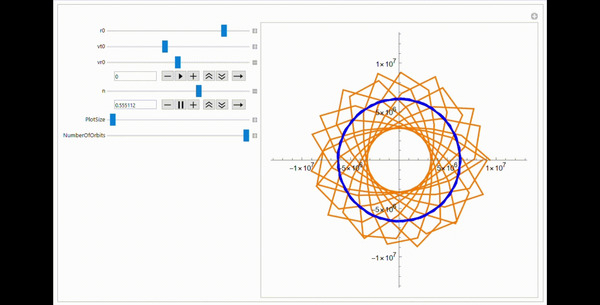
Замкнутый эллипс. Это как раз стабильная орбита. Эллипс может быть чуть-чуть разомкнутым, об этом написал выше
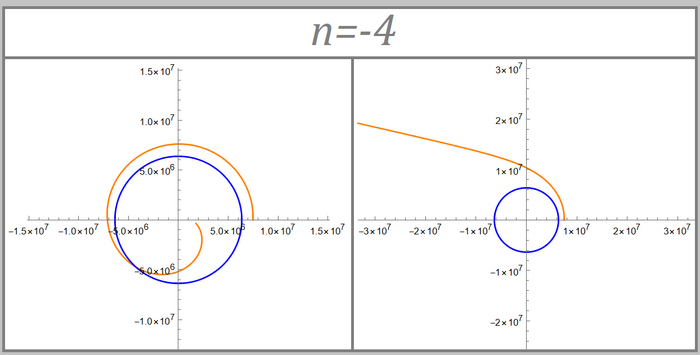
И теперь скроллим все две с половиной тысяч графиков и смотрим на них. Пока прикреплю пару примеров:
Второй тип траектории. Видны очень большие значения координат на осях
Эллипс, который "не шмог" ) Неизвестно, какой у него перигей, но вот апогей оказался выше границы сферы тяготения, поэтому на такую траекторию в реальности все же не выйти. Ах да, это третий тип
Еще один довольно причудливый график. Здесь спутник вышел из атмосферы, сделал виток и упал на Землю (об этом говорит последний кусок траектории), после чего полетел далеко-далеко от Земли. Ну и это второй тип траектории
Как вы могли заметить, я не привел пример 4 типа графиков. А все потому что таковых не было. Хоть выборка и довольно грубая (шаг аж в 500 м/с), она дает понять, что скорее всего выйти на орбиту без включения двигателей не получится (на самом деле то довольно много есть итераций, в которых спутник покинул атмосферу, но потом упал на Землю). Что ж, удручающе, хотелось найти какое-нибудь решение. Хоть и такой результат неудивителен
Как все же можно выйти на орбиту?
Но представим, что нам ну очень хочется на орбиту. Мы уже и пушку купили, и спутник. Логичным становится то, что к спутнику нужно приделать ступень. Представили, что приделали, теперь надо узнать, как из пушки нужно выстрелить и сколько надо дельты
Пусть мы хотим выйти на круговую орбиту радиусом R + R0. Если в описанной прежде системе закрепить угол наклона к горизонту и менять только скорость, то можно заметить, что при росте скорости растет апогей (ну то есть высота апогея от скорости - функция монотонная). А значит, для данного угла существует только одно значение скорости, которому соответствует требуемое значение апогея. Тогда общее множество решений для случая, когда апогей равен R, является некоторой кривой (при решении R(t) = R + R0 это будет поверхность t(v0, a), и это будут все траектории, проходящие через R + R0. Так как при увеличении скорости растет апогей, то нам для каждого угла a нужна одна скорость, которая будет минимальна для этого угла a в t(v0, a). А это как раз и получается кривая)
Теперь из этого множества решений нужно взять одно подходящее. И оно соответствует той комбинации угла наклона и начальной скорости, при которой последняя будет минимальна. Это следует из того, что с ростом скорости максимальное значение силы сопротивления воздуха растет квадратично, а скорость в апогее - приблизительно линейно. В данном случае увеличение скорости незначительно понизит нужную дельту (линейно уменьшится), зато сильно повысит массу конструкции спутника и ступени (будет также увеличиваться квадратично). Учитывая сильный рост массы конструкции, чтоб дельты было достаточно, нужно будет также увеличить начальную массу по сравнению со случаем для минимальной скорости (это следует из того, что нужная дельта убывает медленнее, чем растет масса конструкции). В итоге получим большие затраты по топливу, материалам для ступени, большие ограничения на спутник из-за перегрузок и большие энергозатраты на запуск из пушки. А это нам не особо надо. Конечно, могут быть случаи, когда подходящая начальная скорость не равна минимальной. Но тут уже нужно конкретно рассматривать конкретную ступень и спутник.
Если сократить, то получим, что для выхода на орбиту нужно решить один из вариантов модели полета из поста (в идеале - трехмерную, используя плотность и коэффициент сопротивления воздуха как функции, полученные интерполяцией, а также учитывая все все все силы, испарение аблятора, моменты и т.д.) в параметрическом виде, причем в полярных координатах (перейти к ним не сложно: выражаем декартовы координаты через произведения радиуса и синусов/косинусов угла/углов -, так что это не проблема), далее найти функцию t(v0, a), удовлетворяющую условию R(v0, a)(t) = R + R0, затем найти кривую, в которой каждому a соответствует минимальная v0 и среди v0, принадлежащих этой кривой, найти либо минимальную v0 (то есть минимальную v0 для t(v0, a)), либо найти такую v0, которая даст минимум массы спутника со ступенью (в большинстве случаев она совпадает с минимальной). Затем по v0 найти a, решить модель с заданными параметрами и уже по ней определить все остальные требования к спутнику (дельта, прочностные характеристики и т.п.). Замечу, что процесс итерационный, так как коэффициент сопротивления воздуха берется из модели аппарата, а модель из характеристик, которые берутся из решения модели полета, для которой нужен коэффициент сопротивления воздуха...
Ну а на этом пост заканчивается, ведь ответы на все вопросы из его начала получены. Надеюсь, читать было интересно, а содержание было понятным. Если есть какие-либо вопросы или что-то оказалось непонятным - пишите в комментариях, постараюсь более подробно разобрать. Буду рад критике, советам и дополнениям к содержанию поста.
Всем добра и с прошедшим Новым годом)