Всё что вам надо знать о 3D печати, но вы боитесь спросить
Зашли как-то математик, ЧПУ-шник и программист в опиумокурильню... А бариста им и говорит: а слабо разработать 3D принтер?
Так родилась DELTA-кинематика
Зашли как-то математик, ЧПУ-шник и программист в опиумокурильню... А бариста им и говорит: а слабо разработать 3D принтер?
Так родилась DELTA-кинематика
Всем доброго времени суток
В школе на уроках физики каждый проходил закон всемирного тяготения: "Сила гравитационного взаимодействия прямо пропорциональна массам взаимодействующих объектов и обратно пропорциональна квадрату расстояния":
Именно при таком законе тяготения мы можем наблюдать привычные нам орбиты (эллипс, гипербола, парабола). Но что, если бы закон был немного другим, как бы тогда выглядели орбиты?
На это мы сейчас и посмотрим. Ну а самый удобный способ посмотреть на ньютоновскую гравитацию - нарисовать орбиты, поэтому именно так будем определять, что было бы, если бы гравитация работала по-другому. А заодно вы сможете сами и без математики покрутить и повертеть эти орбиты, в конце поста оставлю файл и инструкцию к нему
Ну и оставлю небольшое уточнение перед прочтением: во всех случаях коэффициенты подобраны так, что сохраняется ускорение свободного падения на Земле (а не ее масса). Сделал это для удобства, иначе была бы куча мучений со скоростями). Ну и да, орбиты вокруг Земли, хотя это не особо важно
Прежде чем начать смотреть на красивые графики и страшные формулы, разберемся, что мы вообще хотим поменять. Ну, очевидно, не гравитационную постоянную, ведь принципиально от этого ничего не изменится. Также очевидно, что и не степени или коэффициенты при массах, так как в таком случае мы по сути будем просто менять константы при формуле, опять-таки, принципиальной разницы не будет
Однако, если менять степень при расстоянии, то вот тогда мы получим принципиальные различия. Ведь сменой степени мы по сути поменяем и характер уравнений, описывающих движение (что будет видно дальше)
Замечу, что еще можно не только что-то менять в самой формуле, но и дополнять ее. Однако способов ее дополнить в значительно раз больше, чем способов изменить, поэтому на все подобные дополнения поста уж точно не хватит. Так что введение чего-то нового в формулу оставлю читателям в качестве упражнения)
Но начнем мы все таки с того, как и почему возникают привычные нам формы орбит. Тут на самом деле все довольно просто, но, как мне кажется, будет полезным показать, как все это дело получается. Записываем уравнения движения в полярной системе координат и решаем их:
Подумайте над тем, откуда берутся исходные уравнения и как константы в конечном уравнении связаны со скоростью и расстоянием до центра в начальный момент времени. Это, так сказать, еще одно упражнение для читателей
Полученное уравнение, хоть это и не выглядит очевидным, описывает кривые второго порядка с фокусом, лежащим в начале системы координат. То есть мы получаем наши привычные эллипсы, гиперболы, параболы (ну и окружности с прямыми). Покрутить их можно здесь. А, ну и пару картинок, как полагается:
Помимо случая с квадратом радиуса есть еще один вариант, для которого можно решить уравнения движения - кубическая зависимость от расстояния. Правда, здесь решение будет более громоздким, поэтому часть выкладок, использованных выше, я опущу:
Во всех трех случаях (кроме 2 при нулевой вертикальной скорости) формулы задают спирали (видно на картинке ниже). Первая, с экспонентами, и вторая при направленной вниз вертикальной скорости дают спирали, которые стремятся к центру планеты (1 и 2 на картинке соответственно). Вторая при направленной вверх вертикальной скорости и третья дают спирали, которые наоборот "уходят" от планеты (4 и 5 соответственно). И только 2 случай при нулевой вертикальной скорости (3 на картинке) дает привычную круглую орбиту
В реальности (ну как реальности, в жизни все таки в уравнениях не куб) вероятность выпадения вот такой удобной конфигурации скоростей (скорость в точности равна первой космической и в точности направлена в горизонт) у спутников да и у чего угодно равна примерно ноль целых хрен десятых, так что с такой гравитацией появление звездных систем просто-напросто невозможно. Поэтому давайте порадуемся за квадрат в наших уравнениях, а то не видать бы нам красивых восходов и закатов, луны на небе, да и года отмерять нечем было бы, нового года бы не отмечали) Правда и отмечать было бы некому)
Ах да, покрутить такие орбиты тоже можно, вот ссыль
Для всех других степеней у расстояния, увы, аналитических решений нет. Но не беда, ведь есть тяжелая артиллерия в виде численного моделирования)
К этому сейчас и приступим, но сперва пошаманим над формулами. Перепишем исходную систему в более общем виде через параметр в степени расстояния, а также перепишем систему так, чтобы заменить время на угол:
Система позволяет моделировать через время, а конечное уравнение - через угол. Пользоваться будем и тем, и тем, в зависимости от того, какая модель будет удобнее
Итак, пишем код для каждой модели
В отличие от моих предыдущих постов, где я выводил набор графиков, здесь я решил добавить ползунки и пользоваться ими. Графики кстати выглядят вот так:
Ну и теперь наконец смотрим на орбиты. Коэффициент при степени я подписал над графиками:
Эти графики я объединил на одной картинке потому, что они не сильно отличаются друг от друга. В целом, для n > -1 графики будут довольно похожи друг на друга, несмотря на различные n. То же самое с графиками у которых n < -3
Вот такая красота получается. Особенно интересными графики выглядят при n > -3, образуя интересные и красивые узоры
А еще смотрите как прикольно витки орбиты "складываются" в окрестности n = -2 (привычная гравитация) и n = 1 (может получиться при привычной гравитации если лететь сквозь равномерный по плотности шар, об это рассказывал здесь):
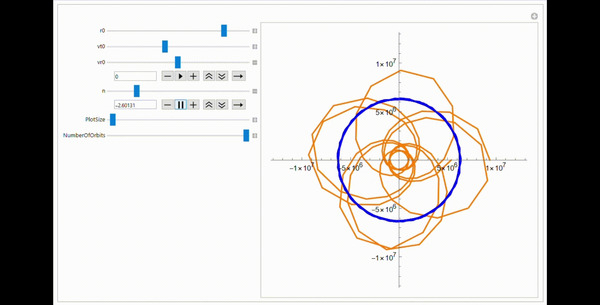
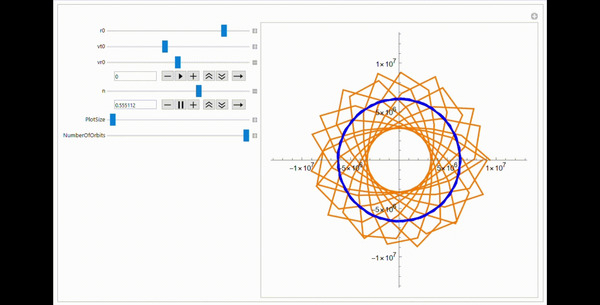
Да, на гифках графики выглядят сильно ломаными, это потому, что Wolfram при изменении параметров делает расчет менее точным, чтобы графики не подвисали и можно было примерно видеть, что будет получаться
Подметим еще два интересных факта:
1. Если буква n не меньше -1, то бессмысленно понятие второй космической, так как она будет бесконечна. Это вытекает из потенциальной энергии на бесконечном расстоянии. Проверить этот факт легко, поэтому оставлю это как еще одно упражнение для читателей)
2. Если n = -1, то первая космическая скорость будет всюду одинакова. Проверить тоже несложно, поэтому также оставлю в качества упражнения для читателей)
Как и обещал, оставлю модели для собственного ковыряния орбит (также можно посмотреть частные случаи в Desmos-е, дублирую ссылки [n=-2], [n=-3]). Обе численные модели вы можете скачать с ЯДиска по этой ссылке (представлены в файле формата .CDF)
Чтобы открыть их, нужно установить себе прогу Wolfram Player (ссыль на оф. сайт, она бесплатная) и запустить через нее скачанный файл
Внутри там все будет написано, так что проблем с пониманием чаво и каво возникнуть не должно. Также не бойтесь, если график становится красным или выдает ошибку, это нормально, связано с "сингулярностями" в некоторых точках при вычислении. Если возникают какие-то проблемы с моделью, либо хотите поменять границы у ползунков - пишите в комментарии, буду исправлять и дополнять. Ну и оставлю картинкой интерфейс программки:
Осматриванием прикольных картинок, ой, то есть путем сложных научных изысканий можно понять, что стоит порадоваться за наш удобный закон тяготения) Ведь при других коэффициентах звездных систем или бы не было, или Вселенная скорее всего не успела бы развиться (для n >= - 1, ну когда второй космической нет), или орбиты были бы такие, что и не разберешься, что за ужас в космосе творится (а то попробуй по тем узорчикам разбери, как гравитация устроена :) )
На такой веселой ноте пост заканчивается. Однако, помимо классического "Надеюсь, было интересно и познавательно, если что-то было непонятно - спрашивайте", хотел бы спросить у вас, как вам добавление упражнений для самостоятельного решения читателями? Мне идея показалась хорошей, так как и материал особо не выдергивается, и есть возможность читающим самим что-то дополнительно повысчитывать, и хотелось бы какой-никакой фидбэк
За сим окончательно откланиваюсь, и всем желаю удачи, счастья, успехов и нормальной гравитации в Новом 2024 году!!!
Всем доброго времени суток
Как можно заметить по названию, идея для этого поста появилась не очень обычно. В ленте мне попался пост из категории жести (ссылка на него, описывать что там не буду, кому надо - тот посмотрит, кому не надо - не прочтет), где в комментариях был вопрос про скорость падения. Ну и раз вы видите этот пост то, я думаю, понимаете, кто взялся за ответ
Начну я не со скорости, а с более интересного - со связи скорости с высотой падения. Это гораздо более общая, более сложная и более интересная задача, о которой и есть смысл рассказать в посте. А уже после этого отвечу на вопросы из "жести", чтобы те, кто пришел только за физикой, могли спокойно пропустить тривиальные и не очень приятные вычисления
В падении на тело действуют две силы: сила тяжести и сила сопротивления воздуха:
С силой тяжести все разобрались еще в школе - классическая формула равноускоренного движения. А вот аэродинамическое сопротивление - штука довольно сложная, и в полностью общем виде аналитических решений не видать. Но, как говорила моя преподавательница по физике, "Физика точна своей неточностью", а потому наложим кое-какие условия, с которыми мы сможем и рыбку съе..., а, в смысле, и аналитически решить, и точность неплохую сохранить. Для этого сначала посмотрим на наш диффур:
Здесь можно сразу заметить, что будет очень удобным назвать все буквы, кроме y, константами. А можно ли так сделать? - Да, вполне. Мы можем признать, что плотность воздуха не зависит от высоты, если расчет проводим для довольно небольших высот (а для них как раз и проводим), мы можем принять коэффициент сопротивления формы постоянным, так как скорость на таких высотах будет сильно ниже скорости звука, мы можем сказать, что площадь миделя будем считать постоянной, предполагая падение в стабильной ориентации. А, ну и еще g назвать константой, но тут это и так понятно
Итак, наше приближение готово, и работать оно будет вполне хорошо для небольших (<~1 км) высот. Теперь приступим к диффуру. А, ну только еще вот этот ворох констант заменим на одну, в остальном все
Первым делом решим его для скорости, тут самое обычное разделение переменных (только сразу учитываем начальные условия):
Конечно, можно было сразу заменить dt = dy / v_y и не париться с решением для времени, однако более длинным способом по пути мы выведем еще и формулы связи со временем, поэтому я предпочту длинное, но более информативное решение
Проинтегрировав скорость по времени, мы получим координату, поэтому берем вытянутую S в одну руку, дифференциал времени в другую и считаем (а, ну и опять начальные условия наложить не забываем, произвольные константы нам не нужны):
Мы получили формулы для скорости и координаты от времени (что кстати довольно приятно, ведь не всегда их можно определить аналитически). Можно ими полюбоваться, можно по ним считать, за какое время какое расстояние пролетит в тот или иной объект, а можно из них получить связь между высотой и скоростью. Мы займемся последним: выразим время через скорость и подставим в формулу для координаты:
И мы полчили довольно маленькую и красивую формулу. Тоже, как по мне, интересный факт: связь координаты со временем и скорости со временем выглядят стремно, зато вместе дают красивый результат. А еще интересно заметить то, как отличаются между собой формулы без учета сопротивления среды и с ее учетом:
Ну и удобно будет посмотреть на расхождение на графике
На этом физика заканчивается, надеюсь вам было интересно узнать про то, как что-либо падает (и как неточна школьная физика, хе-хе), если есть вопросы или дополнения - пишите в комментарии, стараюсь всегда и всем отвечать
Ну а теперь я перейду к ответу на тот пост
Перед тем, как приступлю к вычислениям, хочу сказать, что событие, безусловно, печальное: родители уже собирались видеть своего ребенка взрослым, да и для пацана близилась взрослая жизнь, универ, тусовки, а тут... Грустно, в общем.
Но начнем наши вычисления. Чтобы приблизительно определить скорость падения, нужно, можно сказать, численно продифференцировать: взять два соседних кадра, посчитать перемещение. Я выбрал следующие два кадра:
На первом кадре проведены следующие построения. Отрезками (белые) проложен рост парня (~135,851 пикселя), желтым отрезком обозначено перемещение (93 пикселя), голубым отрезком проложена длина ступеньки у подъезда (~21,932 пикселя)
Все эти длины мы сейчас свяжем с метрами. Длина ступеньки согласно данным из интернета должна составлять 300 мм, ввиду искажения при съемке возьмем 250 мм, откуда отношение между метрами и пикселями (далее обозначу за k) будет равно 0,011399 м/пикс. Да, значение не совсем точное из-за искажения изображения, но погрешность будет не слишком большая. Также определим k, соотнеся с ростом парня. На глаз рост составляет ~165-170 см, с учетом того, что из-за поворота размер искажается, примем для соотношения рост в 150 см, тогда k = 0,011042 м/пикс. Чтобы повысить точность, будем использовать среднее арифметическое двух полученных значений. Тогда по итогу k = 0,0112205 м/пикс., а перемещение составит ~ 1,044 м. А тогда скорость приближенно равна 31,64 м/с.
Теперь на основе общей формулы из начала поста можем узнать, с какой высоты упал десятиклассник. Установившаяся скорость свободного падения по данным из интернета составляет около 55 м/с. Тогда несложно вычислить c для общей формулы:
Подставляя скорость, коэффициент сопротивления и ускорение свободного падения, получим высоту в 70 м, что составляет ~25 этажей (округление в меньшую сторону). Число этажей выглядит довольно значительным, и, вероятно, является слегка завышенным, так как выведенная формула требует постоянства коэффициента сопротивления, чего при подобном падении достичь невозможно. Ну и также 55 м/с (предельная скорость) - это для падения "плашмя", на фото человек летит не так. Скинув в 2,5 раза (цифра примерная и на глаз исходя из изменения миделевого сечения при падении боком)) коэффициент сопротивления получим 54,7 м или 20 этажей. Возможно, цифра еще меньше, но тут я упираюсь в погрешность при подсчете скорости и в собственные (масса, коэффициент сопротивления, площадь миделя) характеристики падавшего, поэтому более точные данные дадут уже только сотрудники органов
На этом пост уже точно заканчивается. Понимаю, что строить научпоп с расчетами вокруг жести не очень хорошее занятие, но надеюсь, что пост не вызовет негатива от читателей. Всем добра, и поменьше бы таких случаев, а в идеале вообще 0
Мне нужна помощь, подсказка.
Хочу собрать круглый подиум (стекло, клей, механизм), чтобы он раскачивался от некоего механизма (направление север-юг). Нечто такое, что можно будет привязать и управлять скоростью (раскачивающийся, баллансирующий). В перспективе это некая светодинамическая домашняя игрушка, которая будет качаться от величины и количества НЧ (бас, темп).
Основа -
Вес - 0.5-+ кг.