Мягкий робот использует механику движения как у растений. (прототип)
Перевод (от ТС):
Он растет, как усик побега, разворачиваясь изнутри наружу, используя пластиковую трубку под давлением. Может растянуться до 72м от стартовой точки. Уникальный дизайн сводит внешнее трение к нулю, позволяя боту перемещаться в сложных средах без каких-либо загвоздок. Он может протискиваться куда угодно, от слоев липкой бумаги до клеевой ванны и узкого коридора с гвоздями.
Может осуществлять самостоятельную навигацию как растение, двигаясь к свету. Для вычисления курса используется видеокамера, выведенная наружу пластиковой кишки, в то время как мелкие воздушные камеры на пластиковой кишке надуваются для поворачивания
(робот перед самым выплевыванием кишки наружу цепляет или надрезает нужные карманы в еще свернутой кишке перед самым ее выходом, хотя это пока прототип и по видео складывается подозрение, что функция толком не реализована, и все повороты и мешочки заранее установлены в кишке в нужных местах, просто чтобы обкатать технологию и понять саму возможность подобного управления - предположение ТС).
Робот вроде этого может юзаться при катастрофах и ЧС. Он достаточно гибок, чтобы протиснуться в крошечные щели и довольно легок, чтобы держаться на воде. Но также он и достаточно силен, чтобы поднимать тяжелые объекты и применять силу, например, чтобы закрыть вентиль. Бот легко преодолевает завалы хлама и мусора, которые затруднили бы перемещение ботам другой топологии.
Другие видео:
Тык
Компиляция всех видео Лиги легенд
Инверсная кинематика (2 сегмента, один эффектор и узел)
Здорово, народ!
Судя по тому, сколько людей ждёт этот пост, деваться особо некуда.
Как и обещал, рассказываю о том, каким образом проводилось вычисление положения частей рук относительно их крепления к туловищу.
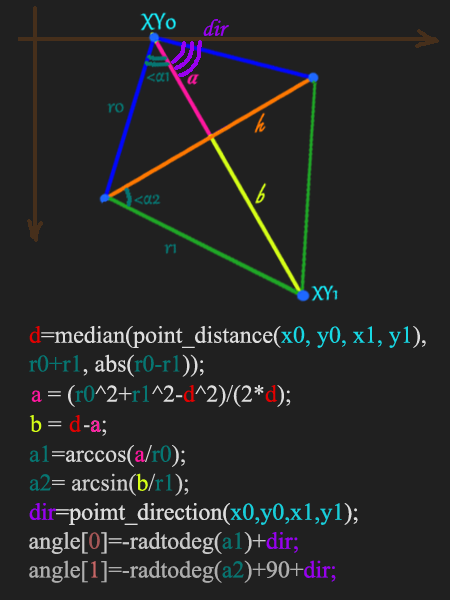
Для начала вообще нужно уяснить, какие данные мы хотим дать игре, чтобы она произвела расчет. У нас всегда есть (по крайней мере, должна быть) х- и y-координата точки крепления руки к телу и длина частей руки. А вот дальше интереснее: если нам дан угол сочленения - то эта прямая кинематика и задача состоит в том, чтобы найти х- и y-координаты кисти воображаемой руки; ну а если даны эти самые координаты - то мы работаем с обратной (инверсной) кинематикой и найти нужно как раз углы, задающие положения сегментов в пространстве.
Как решать?
Для начала d - это расстояние от XY0 до XY1, но с небольшой оговоркой. Нельзя допустить, чтобы d было больше суммы длин наших сегментов, потому что при d равном этой величине мы получим максимально возможный угол - развернутый (180 градусов). Также резонно указать нижнюю границу, модуль разности длин сегментов вполне подойдет.
Получив а и b, работаем с прямоугольными треугольниками и получаем значения углов в радианах. Для того, чтобы их применить на ручках, остается только перевести их в градусную меру и прибавить к ним отклонение от оси ОХ (расчет углов ведется против часовой стрелки, поэтому чтобы направить ручки вниз, отнимаем их от дефолтных 0 градусов).
Важно: здесь мы никак не задаем ограничение на поворот вокруг XY0.
Для удобства можно вогнать это всё в скрипт:
GML: script get_angle
var x1=argument0, y1=argument1, x2=argument2, y2=argument3, r0=argument4, r1=argument5,GML: вызов скрипта get_angle (пример):
d=median(point_distance(x1, y1, x2, y2), r0+r1, max(r0, r1)-min(r0, r1);
var a, b, dir, angle;
a=(sqr(r0)-sqr(r1)+sqr(d))/(2*d)
b=d-a
dir=point_direction(x1, y1, x2, y2)
angle[0]=-radtodeg(arccos(a/r0)+dir
angle[1]=-radtodeg(arcsin(b/r1))+dir+90;
return angle
langle=get_angle(xl,yl,xr+lengthdir_x(38, arms_angle),yr+7+lengthdir_y(38, arms_angle)-8,r0,r1);
Возникает вопрос, а какие точки можно использовать в качестве XY1?
Такой скрипт можно использовать для разных целей.
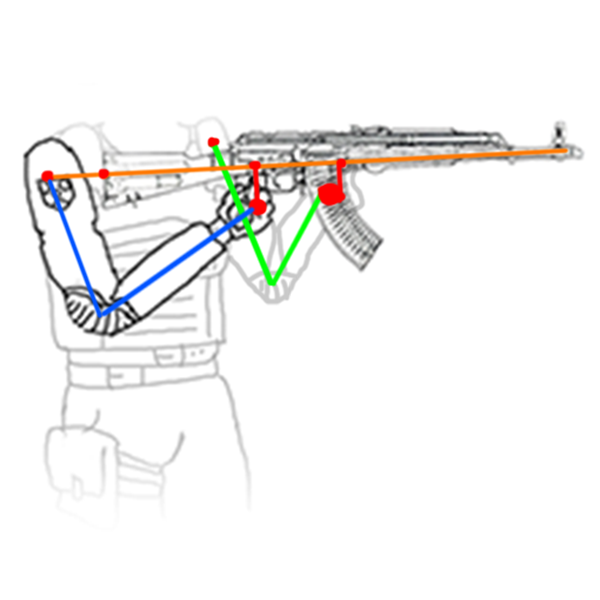
Вот, допустим, нам нужно, чтобы игрок держал автомат с упором к плечу. В таком случае естественно, что он будет держаться руками на рукоятку и цевье/магазин.
Если упором является плечо, то резонно будет осью считать саму точку упора. Оружие будет вращаться вслед за мышью по этой оси.
Например, для правой руки с координатами крепления rx1,ry1, вызов скрипта будет выглядеть так:
GML: get_angle для правой руки, отрисовка:
rangle=get_angle(xr,yr,xr+lengthdir_x(30, arms_angle),yr+lengthdir_y(30, arms_angle),r0,r1)
Xright=xr+lengthdir_x(r0, rangle[0])*player_xscale;
Yright=yr+lengthdir_y(r0, rangle[0]);
draw_sprite_ext(kombineson[4], 1, Xright, yr+lengthdir_y(l1, rangle[0])+sinready, 1, 1, rangle[1], c_white, 1)
draw_sprite_ext(kombineson[4], 0, xr, yr+sinready, 1, 1, rangle[0], c_white, 1)
Где 30 - это длина в пикселях от плечевого упора до рукоятки, за которую держится кисть.
Что примечательно, левая рука при прибавлении к координатам lx1,ly1 поправки будет ориентироваться на место крепления правой руки, так как ось вращения автомата с самой левой рукой никакой связи, кроме как точки lx2,ly2, не имеет:
GML: get_angle для левой руки, отрисовка:
langle=get_angle(xl,yl,xr+lengthdir_x(38, arms_angle),yr+7+lengthdir_y(38, arms_angle)-8,r0,r1)
Xleft=xl+lengthdir_x(r0, langle[0])*player_xscale;
Yleft=yl+lengthdir_y(r0, langle[0]);
draw_sprite_ext(kombineson[3], 0, xl, yl+sinready, 1, 1, langle[0], c_white, 1)
draw_sprite_ext(kombineson[3], 1, Xleft, Yleft+sinready, 1, 1, langle[1], c_white, 1)
Где 38 - это расстояние от плечевого упора до передней части магазина, к которой и крепится lx2,ly2.
Принципиальных отличий в алгоритме при реализации на других ЯП вроде как нет.
Надеюсь, пост окажется полезным для ваших собственных разработок!
Всем добра и до скорого!