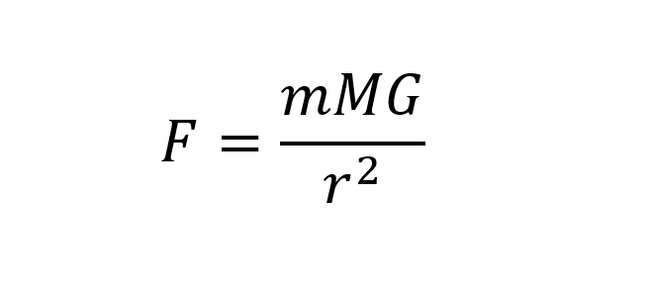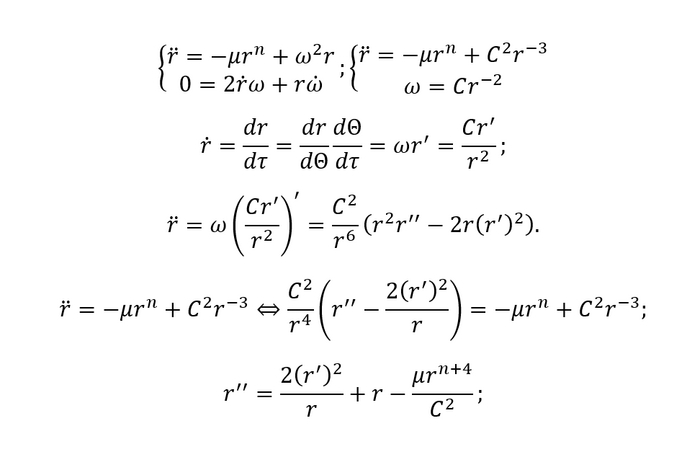Что больше - "е" в степени "Пи" или "Пи" в степени "е"?
Просто решил выложить решение небольшой интересной задачки.
Все сводится к исследованию функции на экстремум, в принципе эту же задачу можно расширить и на другие числа, например е^100 и 100^e, а если очень постараться то и на a^b и b^a
Проект Эйлера: Когда тривиальные задачи с CodeWars надоели и хочется настоящих головоломок
Привет друзья! Если вы не любитель математики или вам неинтересно разбираться в дебрях формул то пропускайте эту статью) если же вам нечем занять свое время нравятся нестандартные задачи, то велком к прочтению!
Сегодня я хочу рассказать вам об одном интересном проекте, который называется Проект Эйлера. Этот проект был создан в честь известного швейцарского математика Леонарда Эйлера и представляет собой серию из 64 математических задач различной сложности. Набор интригующих задач по математике и программированию, для решения которых, однако, недостаточно одной только математической интуиции. Разумеется, математика поможет прийти к красивому и элегантному решению, но для успешного решения большинства задач без навыков программирования не обойтись.
Ссылка на русскоязычный сайт - тык
Создатели проекта - группа энтузиастов, во главе которой стоит Джозеф Синклер. Он же является основателем сайта ProjectEuler (оригинал на английском), на котором можно найти все задачи и ответы к ним. Проект был запущен в 2001 году, и с тех пор его популярность только растет.
Все задачи в Проекте Эйлера разделены на уровни сложности. Начинающим участникам предлагаются задачи начального уровня, для решения которых достаточно знаний арифметики. Продвинутые участники могут попробовать свои силы в решении задач продвинутого уровня, требующих глубоких знаний в области теории чисел, комбинаторики и других разделах математики.
Математические задачи в программировании полезны тем, что они помогают развивать логическое мышление и умение решать проблемы. Кроме того, они учат работать с числами, анализировать данные и создавать алгоритмы. Это очень важные навыки для любого программиста.
Если вы интересуетесь Python и хотите узнать больше об этом языке программирования, то приглашаю вас подписаться на мой канал! https://t.me/python_scrypt
Я буду делиться полезными материалами, уроками и новостями из мира программирования. Подписывайся, и мы будем вместе продвигаться сквозь дебри кода Python!
Помощь
Как настроить выход с помощью модуляции второстепенных переходов каскада
Много было по этому поводу споров и, как я понял, к единому мнению так никто и не пришел. Не вижу смысла описывать вводную часть скважных переходов в виду распространенности этой проблемы. В этом посте я постараюсь рассказать свое видение решения этого вопроса и начать нужно с того, что блоки информации которые поступают из выходного сигнала стоит интерпретировать не как константу, а как разрозненные пакеты с переменной составляющей. Если рассматривать каждый пакет по отдельности, то положительные и отрицательные каскады будут иметь не определенный характер и по этому в таблице переменных мы будем видеть нисходящую волну ниже третьего уровня по Скендфилду. С другой стороны электронный потенциал в поле ионного и пост- ионного выхода показывает нам что быстрые вылеты никак не влияют на закрытие поля. А вообщем, то что я написал выше, не имеет никакого смысла. Все термины выдуманы и не имеют никакого отношения к науке. С наступающим!)
Что если бы гравитация работала по-другому?
Всем доброго времени суток
В школе на уроках физики каждый проходил закон всемирного тяготения: "Сила гравитационного взаимодействия прямо пропорциональна массам взаимодействующих объектов и обратно пропорциональна квадрату расстояния":
Именно при таком законе тяготения мы можем наблюдать привычные нам орбиты (эллипс, гипербола, парабола). Но что, если бы закон был немного другим, как бы тогда выглядели орбиты?
На это мы сейчас и посмотрим. Ну а самый удобный способ посмотреть на ньютоновскую гравитацию - нарисовать орбиты, поэтому именно так будем определять, что было бы, если бы гравитация работала по-другому. А заодно вы сможете сами и без математики покрутить и повертеть эти орбиты, в конце поста оставлю файл и инструкцию к нему
Ну и оставлю небольшое уточнение перед прочтением: во всех случаях коэффициенты подобраны так, что сохраняется ускорение свободного падения на Земле (а не ее масса). Сделал это для удобства, иначе была бы куча мучений со скоростями). Ну и да, орбиты вокруг Земли, хотя это не особо важно
Что будем менять в гравитации?
Прежде чем начать смотреть на красивые графики и страшные формулы, разберемся, что мы вообще хотим поменять. Ну, очевидно, не гравитационную постоянную, ведь принципиально от этого ничего не изменится. Также очевидно, что и не степени или коэффициенты при массах, так как в таком случае мы по сути будем просто менять константы при формуле, опять-таки, принципиальной разницы не будет
Однако, если менять степень при расстоянии, то вот тогда мы получим принципиальные различия. Ведь сменой степени мы по сути поменяем и характер уравнений, описывающих движение (что будет видно дальше)
Замечу, что еще можно не только что-то менять в самой формуле, но и дополнять ее. Однако способов ее дополнить в значительно раз больше, чем способов изменить, поэтому на все подобные дополнения поста уж точно не хватит. Так что введение чего-то нового в формулу оставлю читателям в качестве упражнения)
Немножко про обычный закон тяготения
Но начнем мы все таки с того, как и почему возникают привычные нам формы орбит. Тут на самом деле все довольно просто, но, как мне кажется, будет полезным показать, как все это дело получается. Записываем уравнения движения в полярной системе координат и решаем их:
Подумайте над тем, откуда берутся исходные уравнения и как константы в конечном уравнении связаны со скоростью и расстоянием до центра в начальный момент времени. Это, так сказать, еще одно упражнение для читателей
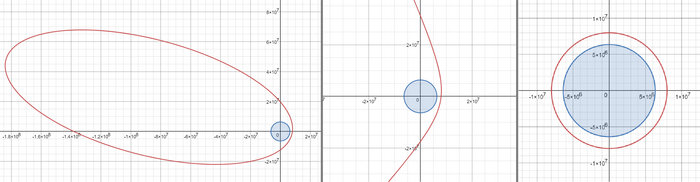
Полученное уравнение, хоть это и не выглядит очевидным, описывает кривые второго порядка с фокусом, лежащим в начале системы координат. То есть мы получаем наши привычные эллипсы, гиперболы, параболы (ну и окружности с прямыми). Покрутить их можно здесь. А, ну и пару картинок, как полагается:
Еще один частный случай закона тяготения
Помимо случая с квадратом радиуса есть еще один вариант, для которого можно решить уравнения движения - кубическая зависимость от расстояния. Правда, здесь решение будет более громоздким, поэтому часть выкладок, использованных выше, я опущу:
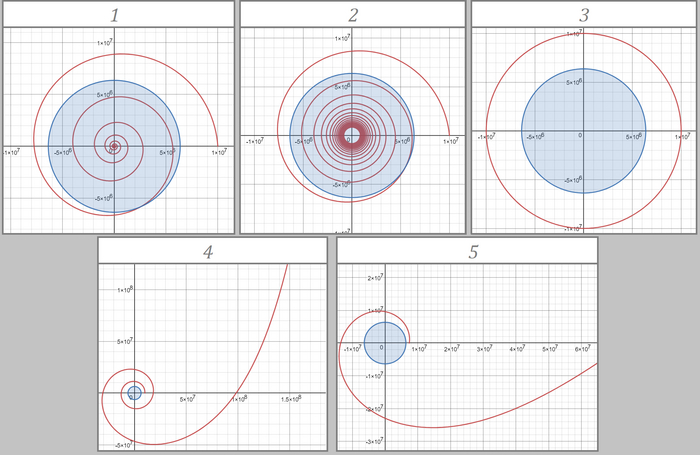
Во всех трех случаях (кроме 2 при нулевой вертикальной скорости) формулы задают спирали (видно на картинке ниже). Первая, с экспонентами, и вторая при направленной вниз вертикальной скорости дают спирали, которые стремятся к центру планеты (1 и 2 на картинке соответственно). Вторая при направленной вверх вертикальной скорости и третья дают спирали, которые наоборот "уходят" от планеты (4 и 5 соответственно). И только 2 случай при нулевой вертикальной скорости (3 на картинке) дает привычную круглую орбиту
В реальности (ну как реальности, в жизни все таки в уравнениях не куб) вероятность выпадения вот такой удобной конфигурации скоростей (скорость в точности равна первой космической и в точности направлена в горизонт) у спутников да и у чего угодно равна примерно ноль целых хрен десятых, так что с такой гравитацией появление звездных систем просто-напросто невозможно. Поэтому давайте порадуемся за квадрат в наших уравнениях, а то не видать бы нам красивых восходов и закатов, луны на небе, да и года отмерять нечем было бы, нового года бы не отмечали) Правда и отмечать было бы некому)
Ах да, покрутить такие орбиты тоже можно, вот ссыль
А что там с остальными степенями
Для всех других степеней у расстояния, увы, аналитических решений нет. Но не беда, ведь есть тяжелая артиллерия в виде численного моделирования)
К этому сейчас и приступим, но сперва пошаманим над формулами. Перепишем исходную систему в более общем виде через параметр в степени расстояния, а также перепишем систему так, чтобы заменить время на угол:
Система позволяет моделировать через время, а конечное уравнение - через угол. Пользоваться будем и тем, и тем, в зависимости от того, какая модель будет удобнее
Итак, пишем код для каждой модели
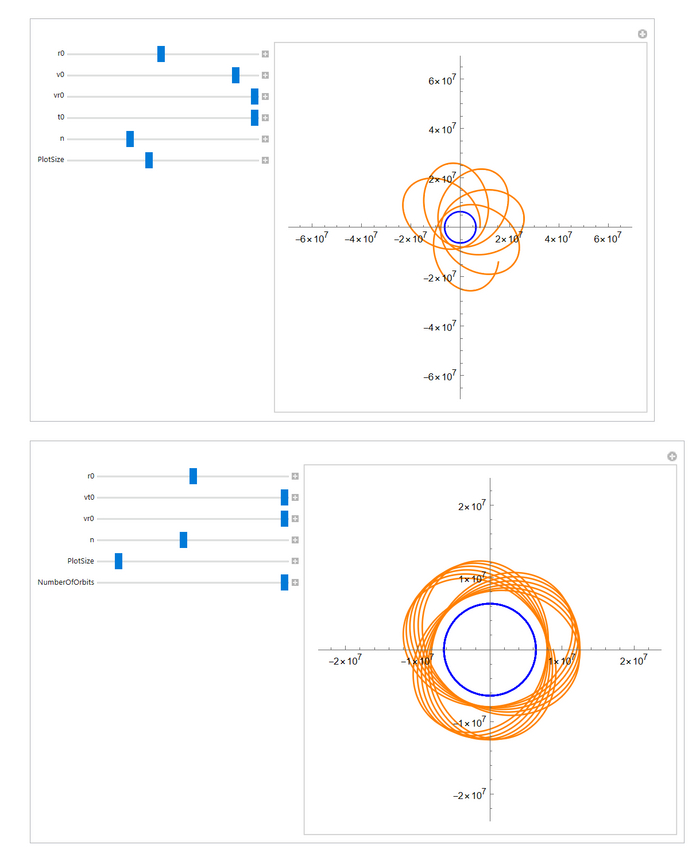
В отличие от моих предыдущих постов, где я выводил набор графиков, здесь я решил добавить ползунки и пользоваться ими. Графики кстати выглядят вот так:
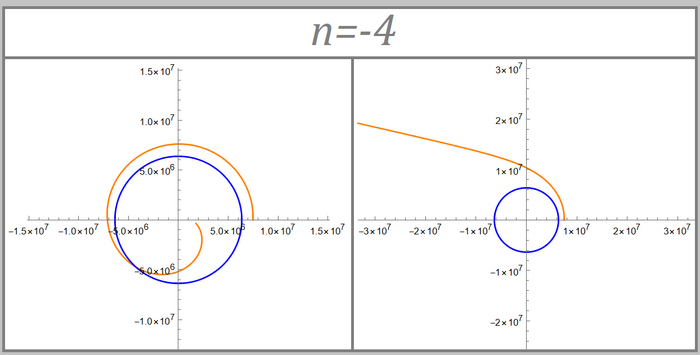
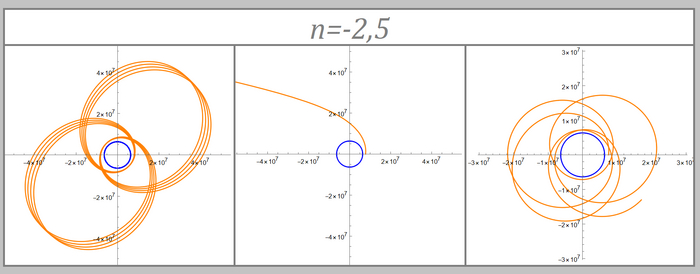
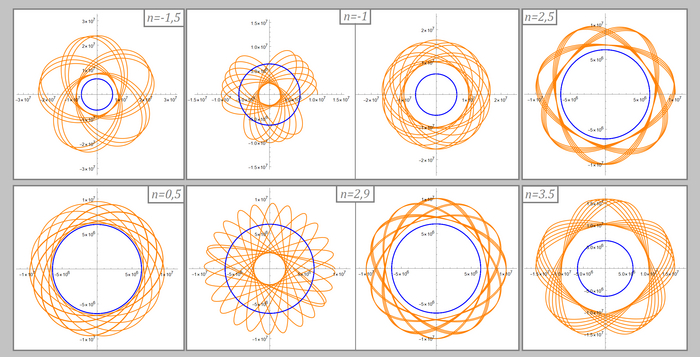
Ну и теперь наконец смотрим на орбиты. Коэффициент при степени я подписал над графиками:
Эти графики я объединил на одной картинке потому, что они не сильно отличаются друг от друга. В целом, для n > -1 графики будут довольно похожи друг на друга, несмотря на различные n. То же самое с графиками у которых n < -3
Вот такая красота получается. Особенно интересными графики выглядят при n > -3, образуя интересные и красивые узоры
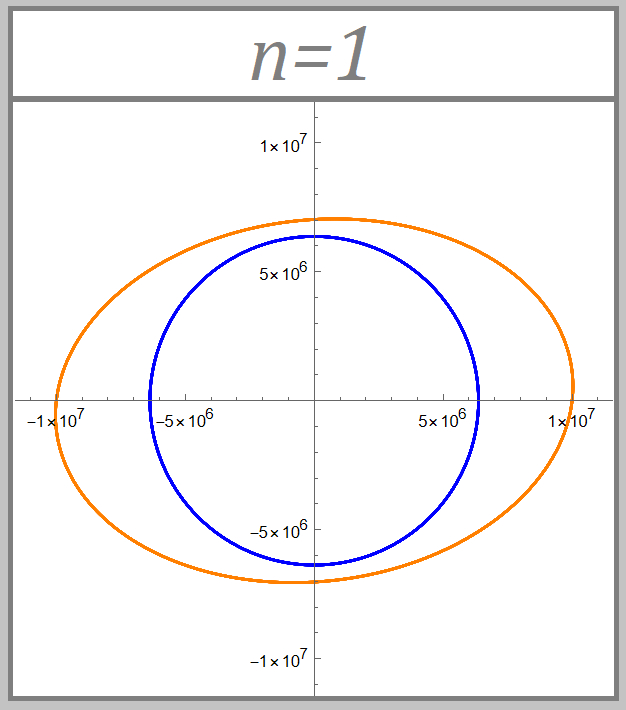
А еще смотрите как прикольно витки орбиты "складываются" в окрестности n = -2 (привычная гравитация) и n = 1 (может получиться при привычной гравитации если лететь сквозь равномерный по плотности шар, об это рассказывал здесь):
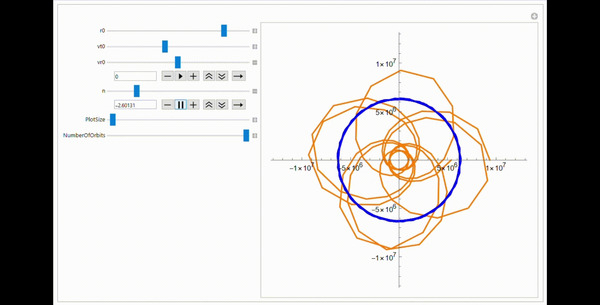
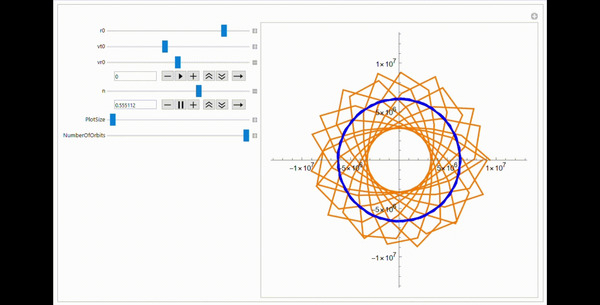
Да, на гифках графики выглядят сильно ломаными, это потому, что Wolfram при изменении параметров делает расчет менее точным, чтобы графики не подвисали и можно было примерно видеть, что будет получаться
Подметим еще два интересных факта:
1. Если буква n не меньше -1, то бессмысленно понятие второй космической, так как она будет бесконечна. Это вытекает из потенциальной энергии на бесконечном расстоянии. Проверить этот факт легко, поэтому оставлю это как еще одно упражнение для читателей)
2. Если n = -1, то первая космическая скорость будет всюду одинакова. Проверить тоже несложно, поэтому также оставлю в качества упражнения для читателей)
Как самому повертеть орбиты?
Как и обещал, оставлю модели для собственного ковыряния орбит (также можно посмотреть частные случаи в Desmos-е, дублирую ссылки [n=-2], [n=-3]). Обе численные модели вы можете скачать с ЯДиска по этой ссылке (представлены в файле формата .CDF)
Чтобы открыть их, нужно установить себе прогу Wolfram Player (ссыль на оф. сайт, она бесплатная) и запустить через нее скачанный файл
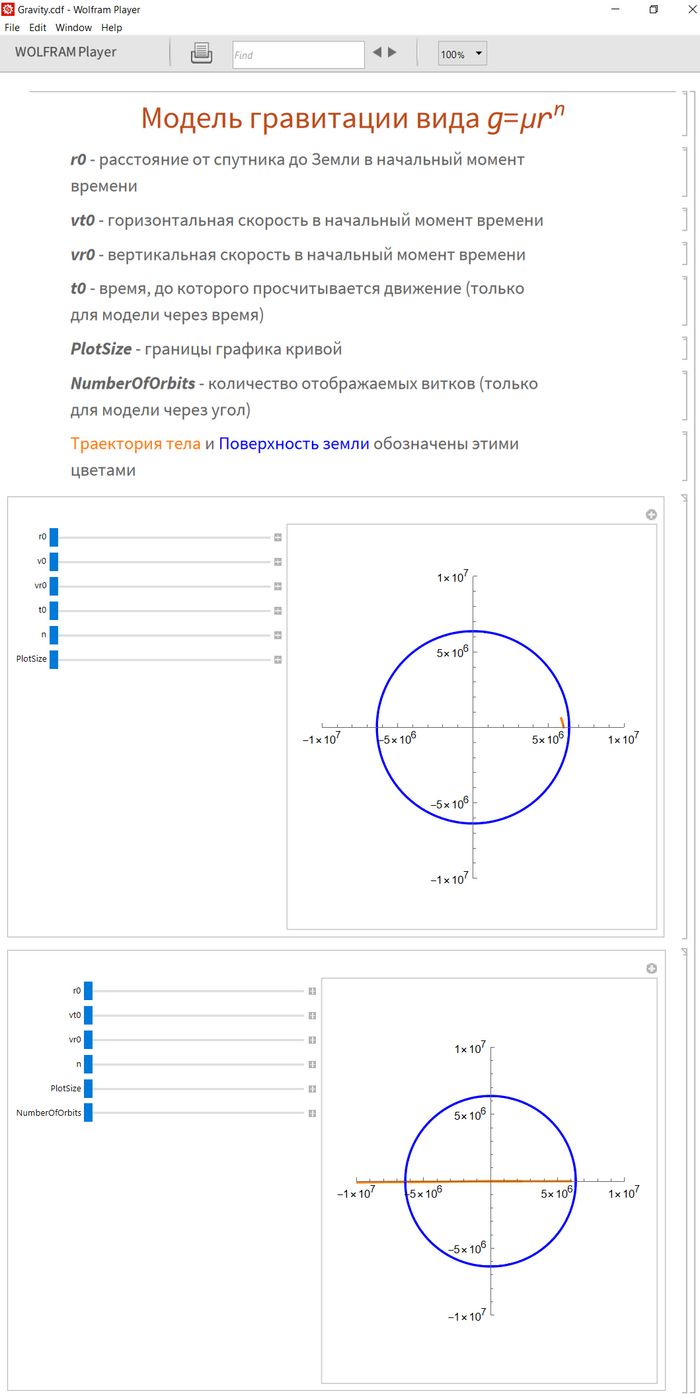
Внутри там все будет написано, так что проблем с пониманием чаво и каво возникнуть не должно. Также не бойтесь, если график становится красным или выдает ошибку, это нормально, связано с "сингулярностями" в некоторых точках при вычислении. Если возникают какие-то проблемы с моделью, либо хотите поменять границы у ползунков - пишите в комментарии, буду исправлять и дополнять. Ну и оставлю картинкой интерфейс программки:
Что по итогу?
Осматриванием прикольных картинок, ой, то есть путем сложных научных изысканий можно понять, что стоит порадоваться за наш удобный закон тяготения) Ведь при других коэффициентах звездных систем или бы не было, или Вселенная скорее всего не успела бы развиться (для n >= - 1, ну когда второй космической нет), или орбиты были бы такие, что и не разберешься, что за ужас в космосе творится (а то попробуй по тем узорчикам разбери, как гравитация устроена :) )
На такой веселой ноте пост заканчивается. Однако, помимо классического "Надеюсь, было интересно и познавательно, если что-то было непонятно - спрашивайте", хотел бы спросить у вас, как вам добавление упражнений для самостоятельного решения читателями? Мне идея показалась хорошей, так как и материал особо не выдергивается, и есть возможность читающим самим что-то дополнительно повысчитывать, и хотелось бы какой-никакой фидбэк
За сим окончательно откланиваюсь, и всем желаю удачи, счастья, успехов и нормальной гравитации в Новом 2024 году!!!
Математический анализ!
Помогите решить задание, пожалуйста! Задание по предмету математический анализ: При помощи линии уровня найти наибольшее и наименьшее значение функции z = x^2 + y^2 в области G: 3x+2y<=6; x >=0; y >=0.