Всем привет! Я продолжаю свою серию постов по популяризации науки :) Пока я выкладываю материалы по теории игр.

Прошлые посты тут:

Игра с природой, или что такое математическое ожидание? : Часть 1, Часть 2

«Дилемма заключенного» – это «игрушечная» игра. Вы можете не ожидать оказаться в такой ситуации, но подобные эффекты окружают нас повсюду. Рассмотрим эту «дилемму» с большим количеством действующих лиц, которую иногда называют «общественной трагедией».

Например, на дорогах бывают пробки, и у меня есть выбор: ехать на работу на машине или на автобусе. Другие участники дорожного движения также будут принимать свои решения. Если я возьму машину, и все решат подобное одновременно, то будет пробка, но в целом все будут сидеть в относительно комфортных персональных автомобилях. Если я поеду на автобусе, то пробка всё ещё никуда не исчезнет (мы предполагаем, что другие участники игры своего решения не поменяли), но я, сидя в автобусе, чувствую себя менее комфортно, да ещё и он не объезжает пробки по обочинам, так что этот результат еще хуже. Если все едут на автобусе, то я, сделав так же, доберусь до работы достаточно быстро и без пробок. Но если я в таких условиях поеду туда на машине, то доберусь так же быстро, но ещё и с комфортом. Таким образом, наличие пробки не зависит от моих действий. У нас тут есть так называемое равновесие Нэша: в данном случае, все рациональные игроки предпочитают ездить на машине (если она у них есть и мы не принимаем во внимание такие дополнительные факторы, как цена бензина, цена билета на транспорт, и т д). Что бы ни делали другие, я лучше выберу машину, потому что не важно, будет ли пробка или нет, я все равно доберусь с большим комфортом, чем если поеду на автобусе. Это доминирующая стратегия. Так что в итоге каждый ездит на своей машине, что мы зачастую видим в крупных городах. Одна из целей государства – сделать общественный транспорт лучшим вариантом для наибольшего числа людей, поэтому существуют городские сборы, парковки и т. д. В этом случае платежные матрицы меняются, и равновесие становится другим.

Еще одна классическая история касается рационального невежества избирателей. Представьте, что вы не знаете результатов выборов заранее. Вы можете изучить программу всех кандидатов, послушать дебаты и проголосовать за лучших. Вторая стратегия заключается в том, чтобы пойти на избирательный участок и проголосовать случайным образом или за того, кого чаще всего видели по телевидению (ну или о ком больше всего слышали от друзей). Каково оптимальное поведение, если мой голос никогда не будет решающим (всё-таки, во Франции, а автор книги говорит именно об этой стране, население составляет 67 миллионов человек)? Конечно, я хочу, чтобы в стране был хороший президент, но я знаю, что больше никто не будет внимательно изучать программы кандидатов. Поэтому не тратить время на эту тему – доминирующая поведенческая стратегия.

Дилемма заключённого в группе. Игра в конкурирующие фирмы.

Поскольку у вас, вероятно, есть несколько друзей, вы можете захотеть попробовать поиграть во что-то, подобное «дилемме заключенного» сразу в группе. Рассмотрим одну из версий дилеммы заключенного в группе.

В аналогичную игру играл профессор Рэймонд С. Батталио из Texas A&M University.

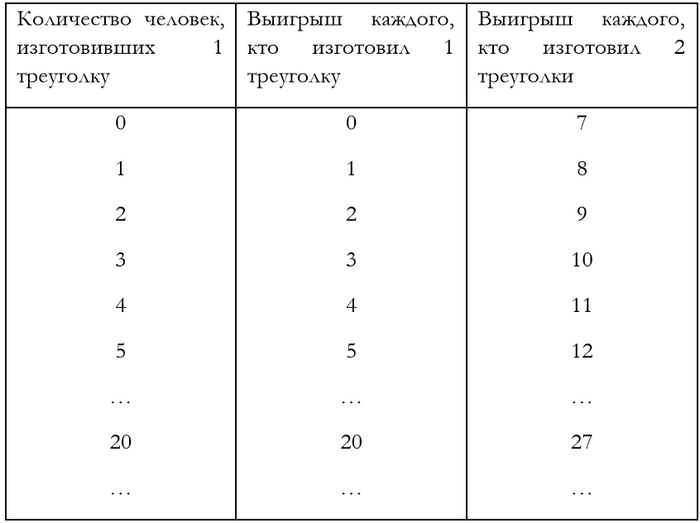
Представим, что все вы – владельцы гипотетических компаний, и все вы должны решить, какой объём продукции, например, треуголок, будет выпускать ваша компания. Это решение нужно написать на листке бумаги, независимо от окружающих (лучше в тайне от них). Листочки надо подписать и кинуть, например, в шляпу.

Если вы хотите выпускать 1 единицу товара, то совокупное предложение сохранится на низком уровне, а, соответственно, цены – на высоком.

Если вы хотите выпускать 2 единицы товара, то вы получите дополнительный доход за счёт других, но цены уменьшатся.

Чтобы не углубляться совсем в экономику, пусть ваш выигрыш будет осуществляться по следующей схеме:

Таким образом, люди, решившие изготовить 2 треуголки, всегда будут получать на 7 баллов больше, чем люди, решившие произвести только одну. Но с другой стороны, чем больше людей решат произвести 2 треуголки, тем ниже их совокупный выигрыш.

Вы также можете снова сыграть в ту же игру, теперь вы должны предварительно обсудить свои стратегии друг с другом.

Изменились ли ваши результаты, когда вы предварительно обсудили свои стратегии? Если да, то с чем это может быть связано?

Эксперименты с реальным денежным выигрышем, проведенные в МФТИ, показали, что большинство участников сделали выбор в пользу производства двух треуголок. Игры для сотрудников RATP Smart Systems были без реального вознаграждения, там выбор участников игры был более однородным (примерно поровну «эгоистов» и «альтруистов»).

Теоретическое и практическое значение этой дилеммы огромно. С теоретической точки зрения это очень просто доказывает, что индивидуальный интерес может резко противоречить интересу коллективному: здесь мы находим явный предел либеральной концепции экономики, постулирующей существование механистической природы («невидимой руки» рынка Адама Смита или «аукциониста» Леона Вальраса), делающей возможным достижение коллективного благополучия исключительно благодаря стремлению к благополучию индивидуальному.

Всем привет! Я продолжаю свою серию постов по популяризации науки :) Пока я выкладываю материалы по теории игр.

Прошлые посты тут:

Игра с природой, или что такое математическое ожидание? : Часть 1, Часть 2

Сегодня, мы перейдём непосредственно к играм рациональных игроков.

Дилемма заключенного

Наверное, самая известная из модельных задач − так называемая «Дилемма заключённого». Она была формализована в 1950 году Альбертом Такером в Принстоне, но сформулирована ещё до него Мерриллом Фладом и Мелвином Дрешером.

Одна из её формулировок звучит следующим образом:

Дилемма заключённого. Окружной прокурор в городе Чикаго знает, что Франкенштейн и Дракула − гангстеры, которые являются виновными в совершении тяжкого преступления, но он не может уличить их в этом, если ни один из них не сознается. Он приказывает арестовать их и по отдельности (да они и так не смогли бы договориться) предлагает каждому следующий контракт:

Если Вы признаете вину, а ваш соучастник не захочет признаться, тогда вы идете домой и вообще свободны, ибо мы сможем забыть, что вы соучастник за ваше признание. Если вы не готовы признать вину, но ваш соучастник признает, то вы будете осуждены и приговорены к максимальному сроку в тюрьме. Если вы оба признаетесь, то вы оба будете осуждены, но не на максимальный срок. Если ни один не признается, то я ненадолго посажу обоих, а за что, уж будьте уверены --- найду.

Здесь речь идет о не очень честном прокуроре, который может сфабриковать дело, чтобы посадить этих персонажей в тюрьму.

При данном условии, Дракула и Франкенштейн играют в некую игру. Для каждого из них есть две стратегии: «Признать вину» и «Молчать».

Условимся записывать каждую возможную ситуацию, как пару выбранных стратегий, где на первом месте стоит выбор Франкенштейна, а на втором − Дракулы. Например, пара («Признать вину», «Молчать») означает, что Франкенштейн заложил Дракулу, который решил, что он добренький.

Так как сидеть в тюрьме, а, особенно, сидеть в тюрьме долго, никому не хочется, будем считать, что цель каждого игрока − минимизировать свой срок заключения. Срок будем записывать в виде чисел, обозначающих потерю очков.

Рассмотрим все возможные ситуации для того, чтобы составить так называемую платёжную матрицу данной игры. В каждой ячейке данной матрицы указана пара чисел, показывающая выигрыши игроков при выборе данной пары стратегий.

Допустим, Франкенштейн выбирает молчание, а Дракула признаётся, тогда Франкенштейна выставляют единственным виновным, и он получает максимальный срок в 10 лет. Мы записываем этот исход как −10 очков для Франкенштейна по стратегии («Молчать», «Признать вину»), и 0 очков для Дракулы по данной стратегии.

Если Франкенштейн признаётся, а Дракула молчит, то Франкенштейна отпускают − записываем Франкенштейну 0 очков по стратегии («Признать вину», «Молчать»), а Дракуле --- −10 очков.

Если же оба решат скрыть все свои тайны, получаем стратегию («Молчать», «Молчать»). По правилам, в таком случае окружной прокурор фабрикует какое-нибудь мелкое дело, и оба идут в тюрьму на 1 год. Записываем −1 очко каждому при данной стратегии.

Наконец, если оба признают вину, то и Франкенштейн и Дракула должны были бы сесть на 10 лет, но так как признание есть смягчающее обстоятельство, то оба в итоге получают по 9 лет. Запишем обоим −9 по стратегии («Признать вину», «Признать вину»).

Мы только что составили матрицу платежей. Сразу введём следующее определение.

Нормальная, или стратегическая форма игры − есть спецификация пространства стратегий и функций выигрышей каждого игрока на всех возможных стадиях игры. Таким образом, игра описывается её платёжной матрицей. Обе стороны матрицы − игроки. Стратегии первого игрока определяются строками, стратегии второго − столбцами, пересечение строк --- выигрыши игроков.

Заметим, что у нас есть проблема: ни Дракула не знает, какую стратегию изберёт Франкенштейн, ни Франкенштейн не знает, какую стратегию изберёт Дракула. Иначе они бы только глянули на соответствующую стратегии другого игрока строку или столбец и выбрали бы лучший исход из предлагаемых им.

В данной игре, на самом деле, всё просто − какую бы стратегию не выбрал соперник, признание всегда ведёт к максимизации очков. Но в таком случае, оба игрока признаются и оба попадут на нары на 9 лет, хотя могли бы оба смолчать и получить всего по 1 году заключения.

Как же так? Почему рациональные действия двух человек привели к настолько нерациональному исходу? А вот это и является дилеммой...

На самом деле, критикам теории игр вообще не нравится дилемма заключенного, потому что они видят, что и Дракуле, и Франкенштейну было бы лучше, если бы они оба молчали. Если бы вместо Франкенштейна поймали подругу Дракулу, Мину Харкер, возможно, они бы так и поступили, но, на самом деле, если люди не связаны до игры, поступки большинства из нас будут достаточно эгоистичными. Если вы посидите на ютубе, вы обнаружите, например, примеры телешоу, основанные на дилемме заключенного, например, шоу «Golden Balls ».

Одна из многочисленных попыток решить парадокс рациональности в дилемме заключенных − это использовать симметрию игры, рассматривая Дракулу и Франкенштейна как близнецов.

Это выглядит следующим образом:

Две рациональных человека, перед которыми стоит одна и та же проблема, придут к такому же выводу. Поэтому Дракула должен исходить из того, что Франкенштейн сделает такой же выбор, как и он. Поэтому либо оба идут в тюрьму на девять лет, или они оба идут в тюрьму на один год. Поскольку последний вариант является предпочтительным, Дракула должен молчать. Так как Франкенштейн его близнец, он будет рассуждать таким же образом и тоже будет молчать.

Но есть одна проблема: это, по сути, превращает данную игру в игру с одним игроком, то есть, дилемма перестаёт быть дилеммой как таковой. Дилемма как раз и заключается в независимости принимаемых игроками решений.

Данная статья относится к Категории 🔮 Появление нового жанра

«Отличие романа от повести, хроники, мемуаров или другой прозаической формы заключается в том, что роман - композиционно замкнутое, протяжённое и законченное в себе повествование о судьбе одного лица или целой группы лиц. Жития святых, при всей разработанности фабулы, не были романами, потому что в них отсутствовал светский интерес к судьбе персонажей, а иллюстрировалась общая идея. […]

Если первоначально действующие лица романа были люди необыкновенные, одарённые, то на склоне европейского романа наблюдается обратное явление: героем романа становится заурядный человек, и центр тяжести переносится на социальную мотивировку, то есть настоящим, действующим лицом является уже общество, как, например, у Бальзака или уЗоля.

Всё это наводит на догадку о связи, которая существует между судьбой романа и положением в данное время вопроса о судьбе личности в истории; здесь не приходится говорить о действительных колебаниях роли личности в истории, а лишь о распространённом ходячем решении этого вопроса в данную минуту, постольку, поскольку оно воспитывает и образует умы современников.

Расцвет романа в XIX веке следует поставить в прямую зависимость от наполеоновской эпопеи, чрезвычайно повысившей акции личности в истории и через БальзакаиСтендаля утучнившей почву для всего французского и европейского романа. Типическая биография захватчика и удачника Бонапарта распылилась у Бальзака в десятки так называемых «романов удачи» (roman de reussite), где основная движущая сила - не любовь, а карьера, то есть стремление пробиться из низших и средних социальных слоев в верхние.

Ясно, что, когда мы вступили в полосу могучих социальных движений, массовых организованных действий, акции личности в истории падают и вместе с ними падают влияние и сила романа, для которого общепризнанная роль личности в истории служит как бы манометром, показывающим давление социальной атмосферы. Мера романа - человеческая биография или система биографий. С первых же шагов новый романист почувствовал, что отдельной судьбы не существует, и старался нужное ему социальное растение вырвать из почвы со всеми корнями, со всеми спутниками и атрибутами; таким образом, роман всегда предлагает нам систему явлений, управляемую биографической связью, измеряемую биографической мерой, и лишь постольку держится роман композитивно, поскольку в нём живёт центробежная тяга планетной системы, поскольку центростремительная тяга, тяга от центра к периферии, не возобладала окончательно над центробежной.

Последним примером центробежного биографического европейского романа можно считать «Жан Кристофа» Ромена Роллана, эту лебединую песнь европейской биографии, величавой плавностью и благородством синтетических приемов приводящую на память «Вильгельма Мейстера» Гёте. «Жан Кристоф» замыкает круг романа; при всей своей современности это - старомодное произведение; в нем собран старинный центробежный мед германской и латинской расы.

Для того, чтобы создать последний роман, понадобилось две расы, сочетавшиеся в личности Ромена Роллана, но этого было всё-таки мало. «Жан Кристоф» приводится в движение тем же мощным толчком наполеоновского революционного удара, как и весь европейский роман, - через бетховенскую биографию Кристофа, через соприкосновение с мощной фигурой музыкального мифа, рождённого тем же наполеоновским половодьем в истории.

Дальнейшая судьба романа будет не чем иным, как историей распыления биографии, как формы личного существования, даже больше чем распыления - катастрофической гибели биографии».

Мандельштам О.Э., Конец романа / Собрание сочинений в 4-х томах, М., «Арт-Бизнес-Центр», Том 2, 1999 г., с. 201-203.

Источник — портал VIKENT.RU

Дополнительные материалы

см. термин Среднеарифметический гражданин в 🔖 Словаре проекта VIKENT.RU

+ Плейлист из 24-х видео: ИНТЕЛЛЕКТУАЛЬНЫЕ РАЗОБЛАЧЕНИЯ от портала VIKENT.RU

+ Ваши дополнительные возможности:Воскресным вечером 02 октября 2022 в 19:59 (мск) на ютуб-канале VIKENT.RU пройдёт онлайн-лекция № 291:

Также, идёт приём Ваших новых вопросов по более чем 400-м направлениям творческой деятельности – на онлайн-консультацию 16 октября 2022 года в 19:59 мск (воскресенье). Это принципиально бесплатный формат.

Изображения в статье

Осип Эмильевич Мандельштам — отечественный поэт / Мандельштамовский центр & Изображение Tumisu с сайта Pixabay

Изображение mohamed Hassan с сайта Pixabay