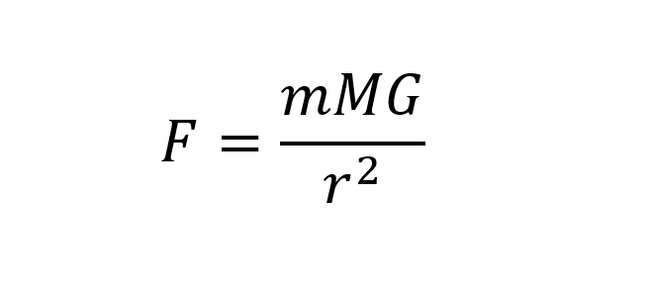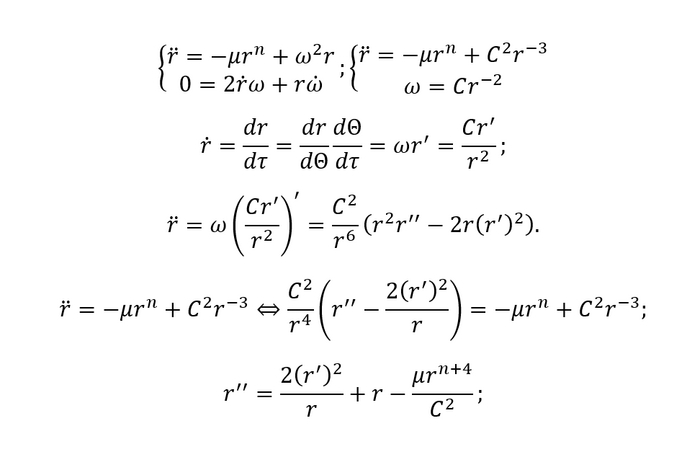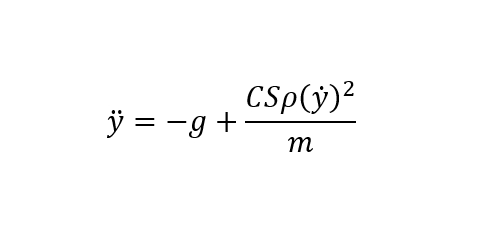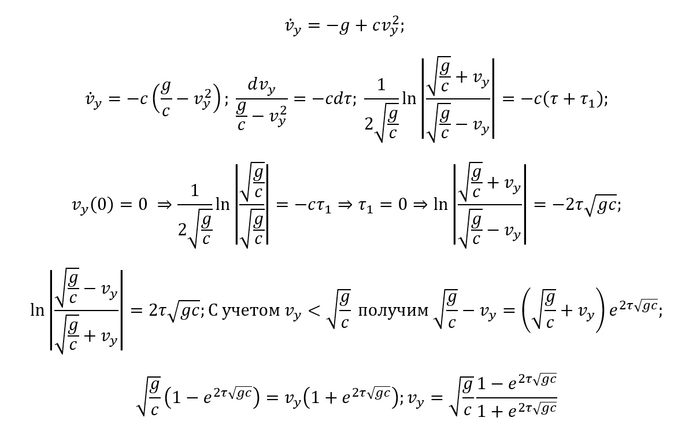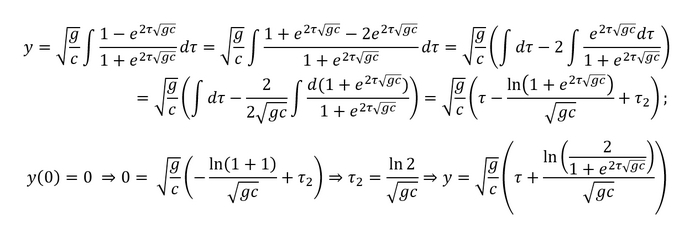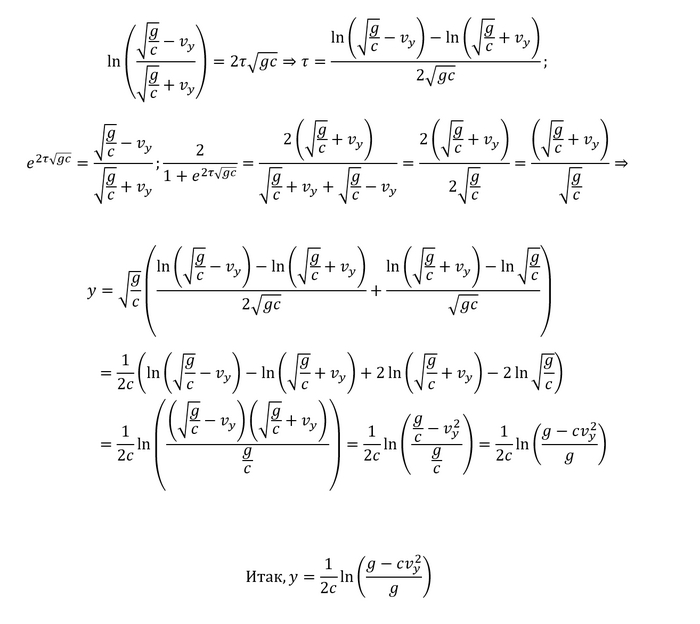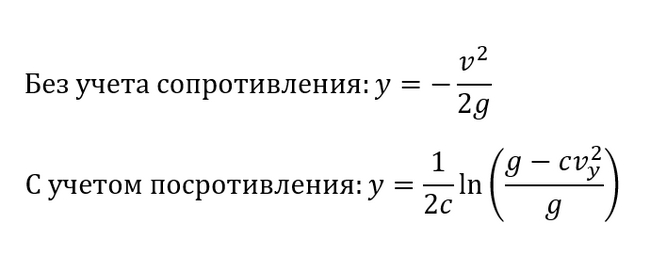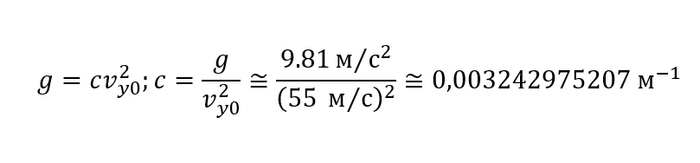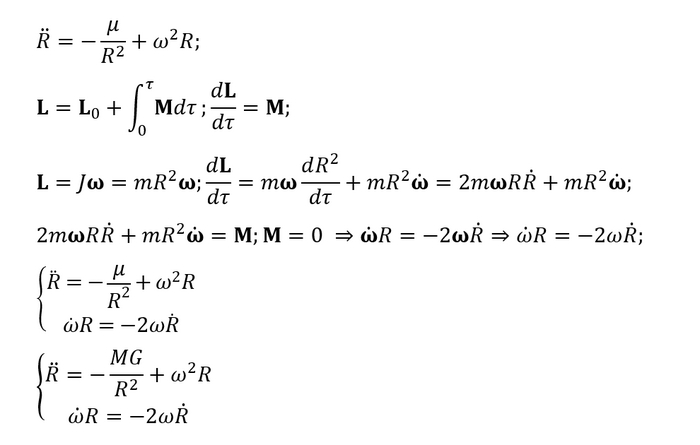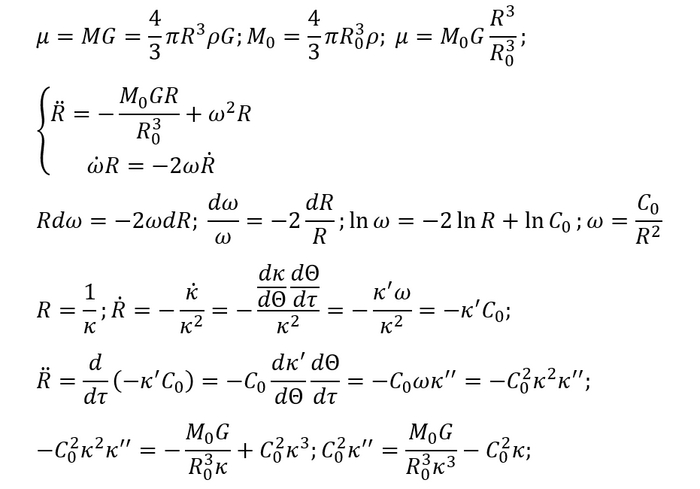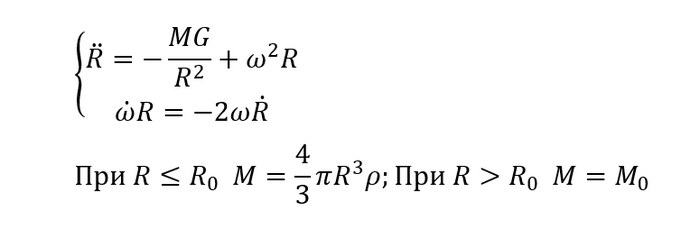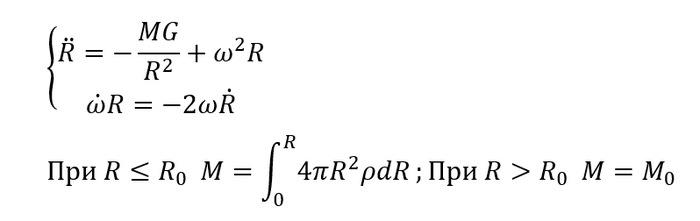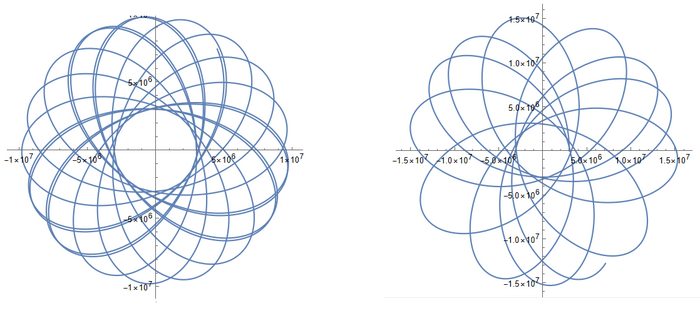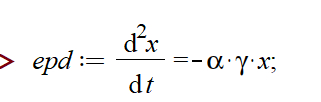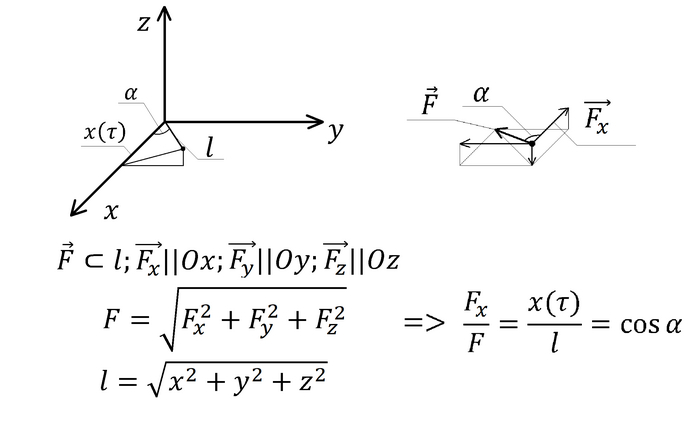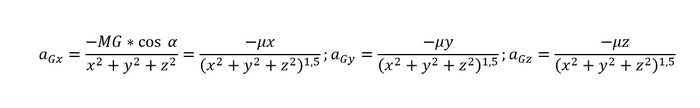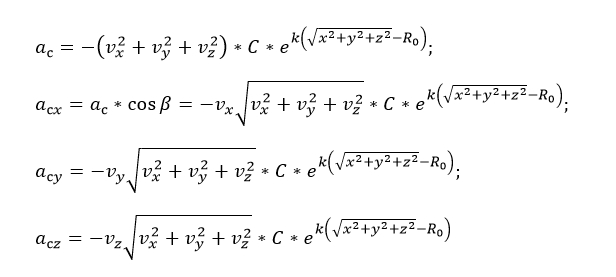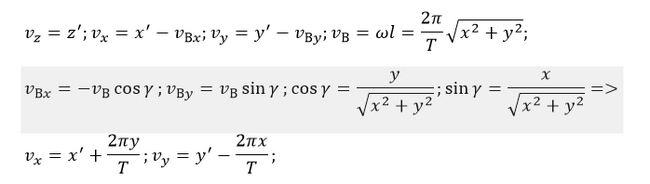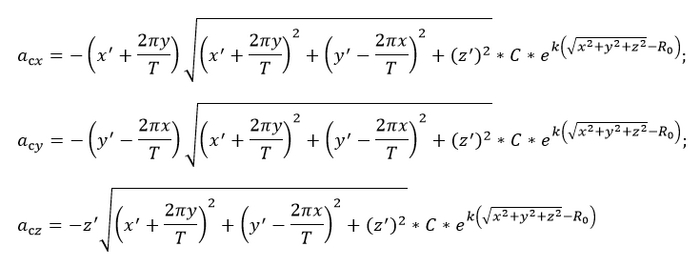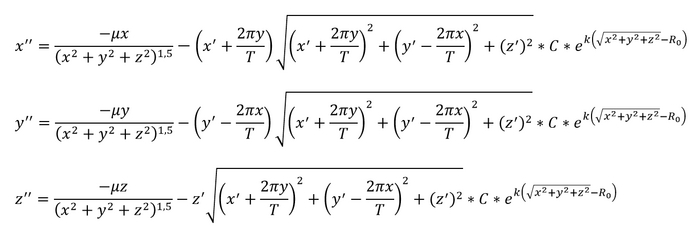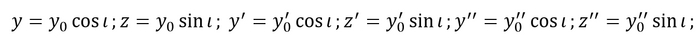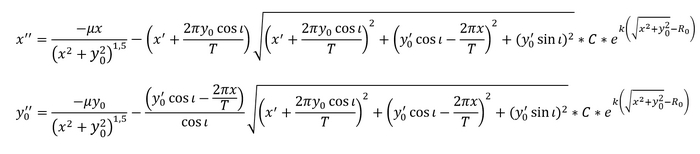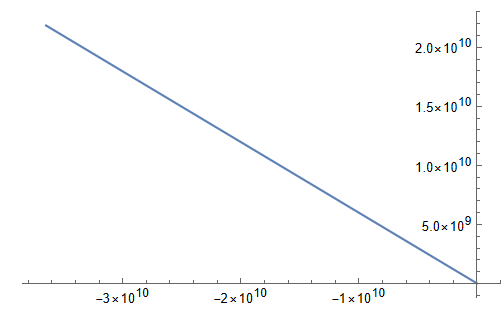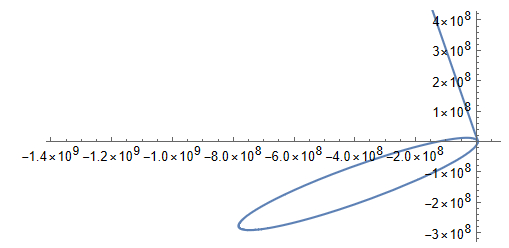Что если бы гравитация работала по-другому?
Всем доброго времени суток
В школе на уроках физики каждый проходил закон всемирного тяготения: "Сила гравитационного взаимодействия прямо пропорциональна массам взаимодействующих объектов и обратно пропорциональна квадрату расстояния":
Именно при таком законе тяготения мы можем наблюдать привычные нам орбиты (эллипс, гипербола, парабола). Но что, если бы закон был немного другим, как бы тогда выглядели орбиты?
На это мы сейчас и посмотрим. Ну а самый удобный способ посмотреть на ньютоновскую гравитацию - нарисовать орбиты, поэтому именно так будем определять, что было бы, если бы гравитация работала по-другому. А заодно вы сможете сами и без математики покрутить и повертеть эти орбиты, в конце поста оставлю файл и инструкцию к нему
Ну и оставлю небольшое уточнение перед прочтением: во всех случаях коэффициенты подобраны так, что сохраняется ускорение свободного падения на Земле (а не ее масса). Сделал это для удобства, иначе была бы куча мучений со скоростями). Ну и да, орбиты вокруг Земли, хотя это не особо важно
Что будем менять в гравитации?
Прежде чем начать смотреть на красивые графики и страшные формулы, разберемся, что мы вообще хотим поменять. Ну, очевидно, не гравитационную постоянную, ведь принципиально от этого ничего не изменится. Также очевидно, что и не степени или коэффициенты при массах, так как в таком случае мы по сути будем просто менять константы при формуле, опять-таки, принципиальной разницы не будет
Однако, если менять степень при расстоянии, то вот тогда мы получим принципиальные различия. Ведь сменой степени мы по сути поменяем и характер уравнений, описывающих движение (что будет видно дальше)
Замечу, что еще можно не только что-то менять в самой формуле, но и дополнять ее. Однако способов ее дополнить в значительно раз больше, чем способов изменить, поэтому на все подобные дополнения поста уж точно не хватит. Так что введение чего-то нового в формулу оставлю читателям в качестве упражнения)
Немножко про обычный закон тяготения
Но начнем мы все таки с того, как и почему возникают привычные нам формы орбит. Тут на самом деле все довольно просто, но, как мне кажется, будет полезным показать, как все это дело получается. Записываем уравнения движения в полярной системе координат и решаем их:
Подумайте над тем, откуда берутся исходные уравнения и как константы в конечном уравнении связаны со скоростью и расстоянием до центра в начальный момент времени. Это, так сказать, еще одно упражнение для читателей
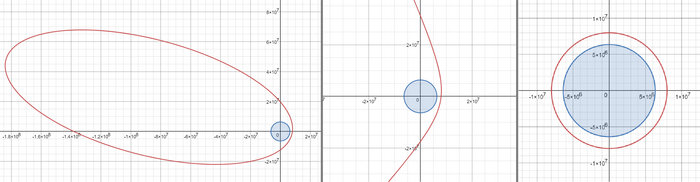
Полученное уравнение, хоть это и не выглядит очевидным, описывает кривые второго порядка с фокусом, лежащим в начале системы координат. То есть мы получаем наши привычные эллипсы, гиперболы, параболы (ну и окружности с прямыми). Покрутить их можно здесь. А, ну и пару картинок, как полагается:
Еще один частный случай закона тяготения
Помимо случая с квадратом радиуса есть еще один вариант, для которого можно решить уравнения движения - кубическая зависимость от расстояния. Правда, здесь решение будет более громоздким, поэтому часть выкладок, использованных выше, я опущу:
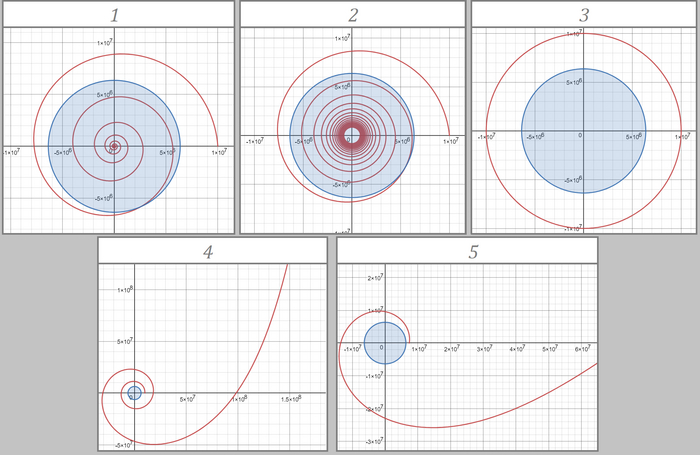
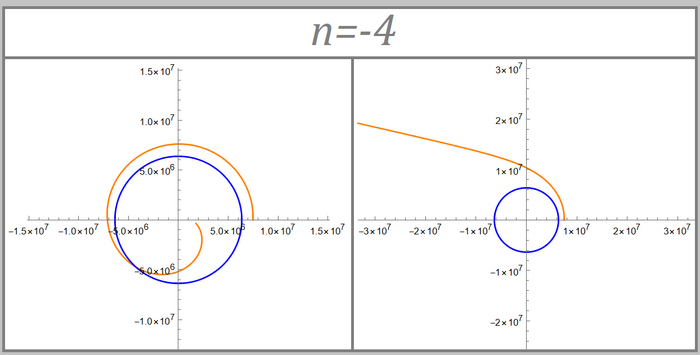
Во всех трех случаях (кроме 2 при нулевой вертикальной скорости) формулы задают спирали (видно на картинке ниже). Первая, с экспонентами, и вторая при направленной вниз вертикальной скорости дают спирали, которые стремятся к центру планеты (1 и 2 на картинке соответственно). Вторая при направленной вверх вертикальной скорости и третья дают спирали, которые наоборот "уходят" от планеты (4 и 5 соответственно). И только 2 случай при нулевой вертикальной скорости (3 на картинке) дает привычную круглую орбиту
В реальности (ну как реальности, в жизни все таки в уравнениях не куб) вероятность выпадения вот такой удобной конфигурации скоростей (скорость в точности равна первой космической и в точности направлена в горизонт) у спутников да и у чего угодно равна примерно ноль целых хрен десятых, так что с такой гравитацией появление звездных систем просто-напросто невозможно. Поэтому давайте порадуемся за квадрат в наших уравнениях, а то не видать бы нам красивых восходов и закатов, луны на небе, да и года отмерять нечем было бы, нового года бы не отмечали) Правда и отмечать было бы некому)
Ах да, покрутить такие орбиты тоже можно, вот ссыль
А что там с остальными степенями
Для всех других степеней у расстояния, увы, аналитических решений нет. Но не беда, ведь есть тяжелая артиллерия в виде численного моделирования)
К этому сейчас и приступим, но сперва пошаманим над формулами. Перепишем исходную систему в более общем виде через параметр в степени расстояния, а также перепишем систему так, чтобы заменить время на угол:
Система позволяет моделировать через время, а конечное уравнение - через угол. Пользоваться будем и тем, и тем, в зависимости от того, какая модель будет удобнее
Итак, пишем код для каждой модели
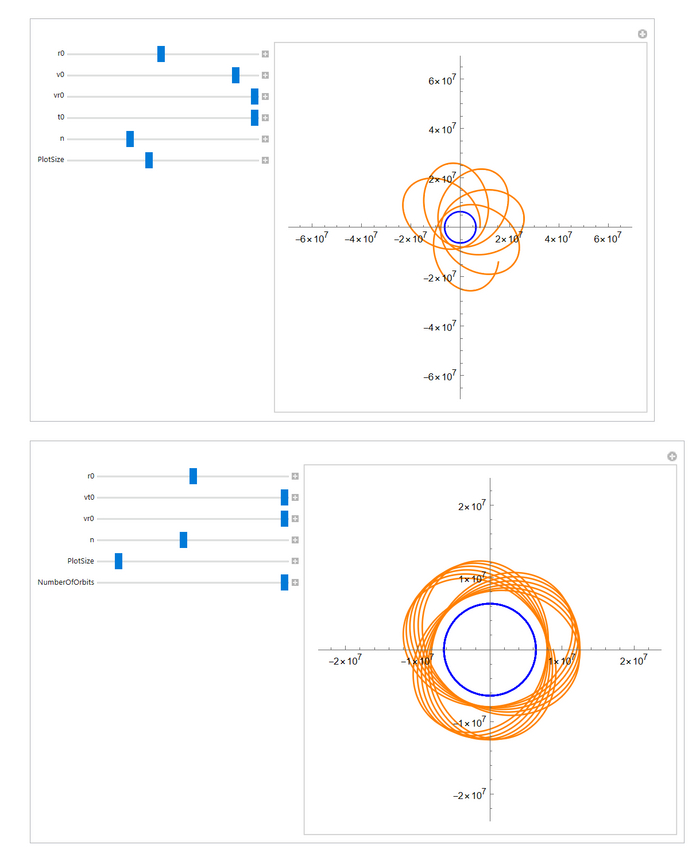
В отличие от моих предыдущих постов, где я выводил набор графиков, здесь я решил добавить ползунки и пользоваться ими. Графики кстати выглядят вот так:
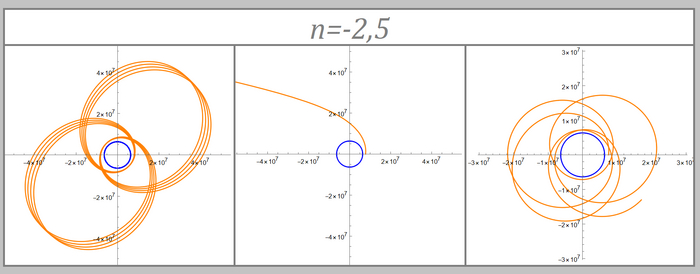
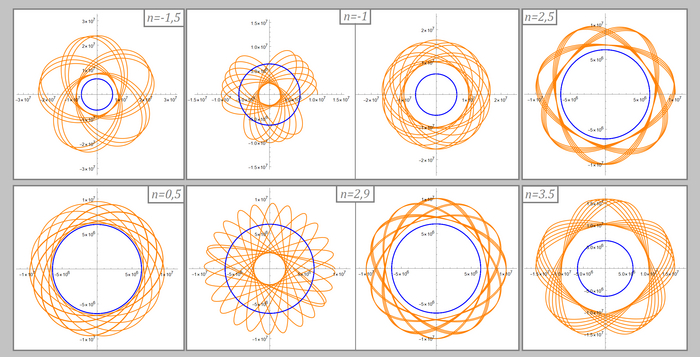
Ну и теперь наконец смотрим на орбиты. Коэффициент при степени я подписал над графиками:
Эти графики я объединил на одной картинке потому, что они не сильно отличаются друг от друга. В целом, для n > -1 графики будут довольно похожи друг на друга, несмотря на различные n. То же самое с графиками у которых n < -3
Вот такая красота получается. Особенно интересными графики выглядят при n > -3, образуя интересные и красивые узоры
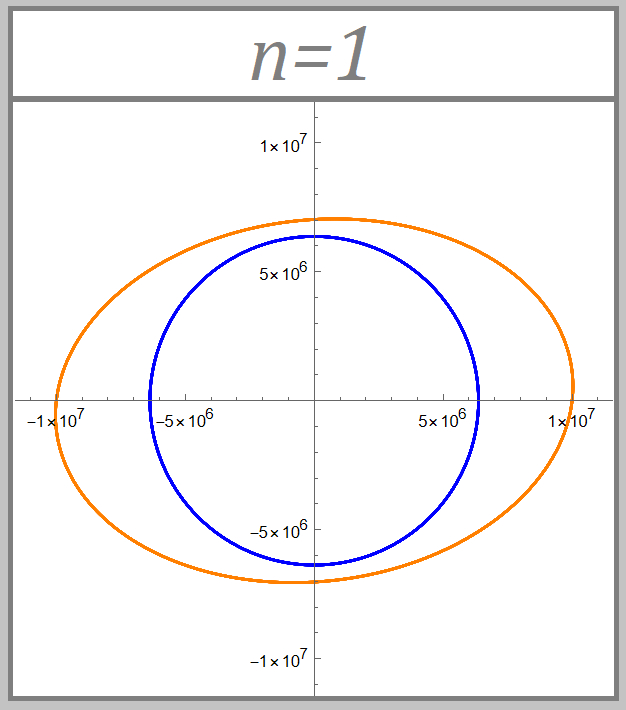
А еще смотрите как прикольно витки орбиты "складываются" в окрестности n = -2 (привычная гравитация) и n = 1 (может получиться при привычной гравитации если лететь сквозь равномерный по плотности шар, об это рассказывал здесь):
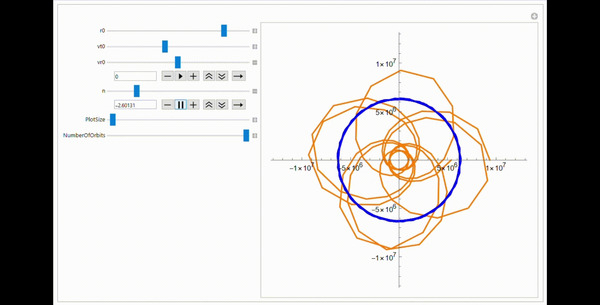
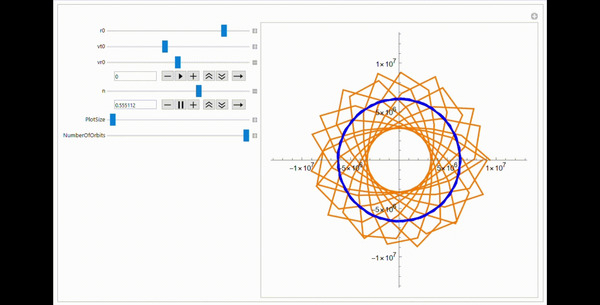
Да, на гифках графики выглядят сильно ломаными, это потому, что Wolfram при изменении параметров делает расчет менее точным, чтобы графики не подвисали и можно было примерно видеть, что будет получаться
Подметим еще два интересных факта:
1. Если буква n не меньше -1, то бессмысленно понятие второй космической, так как она будет бесконечна. Это вытекает из потенциальной энергии на бесконечном расстоянии. Проверить этот факт легко, поэтому оставлю это как еще одно упражнение для читателей)
2. Если n = -1, то первая космическая скорость будет всюду одинакова. Проверить тоже несложно, поэтому также оставлю в качества упражнения для читателей)
Как самому повертеть орбиты?
Как и обещал, оставлю модели для собственного ковыряния орбит (также можно посмотреть частные случаи в Desmos-е, дублирую ссылки [n=-2], [n=-3]). Обе численные модели вы можете скачать с ЯДиска по этой ссылке (представлены в файле формата .CDF)
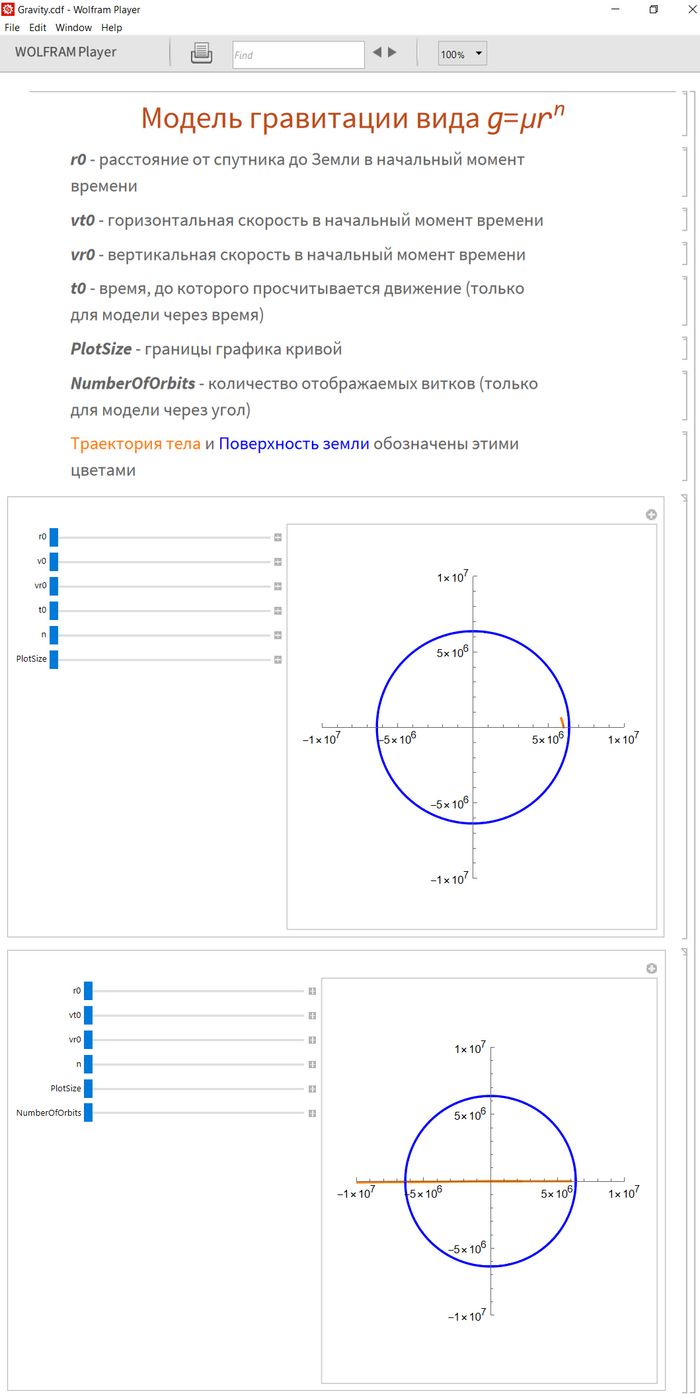
Чтобы открыть их, нужно установить себе прогу Wolfram Player (ссыль на оф. сайт, она бесплатная) и запустить через нее скачанный файл
Внутри там все будет написано, так что проблем с пониманием чаво и каво возникнуть не должно. Также не бойтесь, если график становится красным или выдает ошибку, это нормально, связано с "сингулярностями" в некоторых точках при вычислении. Если возникают какие-то проблемы с моделью, либо хотите поменять границы у ползунков - пишите в комментарии, буду исправлять и дополнять. Ну и оставлю картинкой интерфейс программки:
Что по итогу?
Осматриванием прикольных картинок, ой, то есть путем сложных научных изысканий можно понять, что стоит порадоваться за наш удобный закон тяготения) Ведь при других коэффициентах звездных систем или бы не было, или Вселенная скорее всего не успела бы развиться (для n >= - 1, ну когда второй космической нет), или орбиты были бы такие, что и не разберешься, что за ужас в космосе творится (а то попробуй по тем узорчикам разбери, как гравитация устроена :) )
На такой веселой ноте пост заканчивается. Однако, помимо классического "Надеюсь, было интересно и познавательно, если что-то было непонятно - спрашивайте", хотел бы спросить у вас, как вам добавление упражнений для самостоятельного решения читателями? Мне идея показалась хорошей, так как и материал особо не выдергивается, и есть возможность читающим самим что-то дополнительно повысчитывать, и хотелось бы какой-никакой фидбэк
За сим окончательно откланиваюсь, и всем желаю удачи, счастья, успехов и нормальной гравитации в Новом 2024 году!!!
Как движется тело в свободном падении или ответ на "Жесть"
Всем доброго времени суток
Как можно заметить по названию, идея для этого поста появилась не очень обычно. В ленте мне попался пост из категории жести (ссылка на него, описывать что там не буду, кому надо - тот посмотрит, кому не надо - не прочтет), где в комментариях был вопрос про скорость падения. Ну и раз вы видите этот пост то, я думаю, понимаете, кто взялся за ответ
Начну я не со скорости, а с более интересного - со связи скорости с высотой падения. Это гораздо более общая, более сложная и более интересная задача, о которой и есть смысл рассказать в посте. А уже после этого отвечу на вопросы из "жести", чтобы те, кто пришел только за физикой, могли спокойно пропустить тривиальные и не очень приятные вычисления
Связь между скоростью и высотой
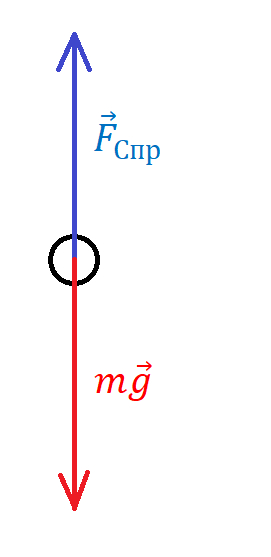
В падении на тело действуют две силы: сила тяжести и сила сопротивления воздуха:
С силой тяжести все разобрались еще в школе - классическая формула равноускоренного движения. А вот аэродинамическое сопротивление - штука довольно сложная, и в полностью общем виде аналитических решений не видать. Но, как говорила моя преподавательница по физике, "Физика точна своей неточностью", а потому наложим кое-какие условия, с которыми мы сможем и рыбку съе..., а, в смысле, и аналитически решить, и точность неплохую сохранить. Для этого сначала посмотрим на наш диффур:
Здесь можно сразу заметить, что будет очень удобным назвать все буквы, кроме y, константами. А можно ли так сделать? - Да, вполне. Мы можем признать, что плотность воздуха не зависит от высоты, если расчет проводим для довольно небольших высот (а для них как раз и проводим), мы можем принять коэффициент сопротивления формы постоянным, так как скорость на таких высотах будет сильно ниже скорости звука, мы можем сказать, что площадь миделя будем считать постоянной, предполагая падение в стабильной ориентации. А, ну и еще g назвать константой, но тут это и так понятно
Итак, наше приближение готово, и работать оно будет вполне хорошо для небольших (<~1 км) высот. Теперь приступим к диффуру. А, ну только еще вот этот ворох констант заменим на одну, в остальном все
Первым делом решим его для скорости, тут самое обычное разделение переменных (только сразу учитываем начальные условия):
Конечно, можно было сразу заменить dt = dy / v_y и не париться с решением для времени, однако более длинным способом по пути мы выведем еще и формулы связи со временем, поэтому я предпочту длинное, но более информативное решение
Проинтегрировав скорость по времени, мы получим координату, поэтому берем вытянутую S в одну руку, дифференциал времени в другую и считаем (а, ну и опять начальные условия наложить не забываем, произвольные константы нам не нужны):
Мы получили формулы для скорости и координаты от времени (что кстати довольно приятно, ведь не всегда их можно определить аналитически). Можно ими полюбоваться, можно по ним считать, за какое время какое расстояние пролетит в тот или иной объект, а можно из них получить связь между высотой и скоростью. Мы займемся последним: выразим время через скорость и подставим в формулу для координаты:
И мы полчили довольно маленькую и красивую формулу. Тоже, как по мне, интересный факт: связь координаты со временем и скорости со временем выглядят стремно, зато вместе дают красивый результат. А еще интересно заметить то, как отличаются между собой формулы без учета сопротивления среды и с ее учетом:
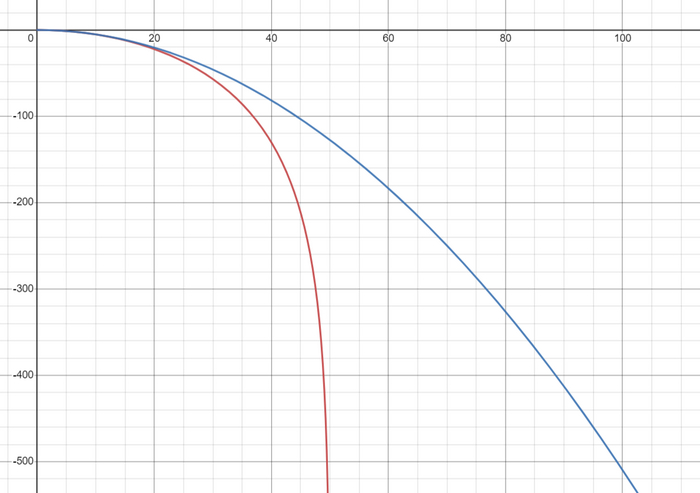
Ну и удобно будет посмотреть на расхождение на графике
На этом физика заканчивается, надеюсь вам было интересно узнать про то, как что-либо падает (и как неточна школьная физика, хе-хе), если есть вопросы или дополнения - пишите в комментарии, стараюсь всегда и всем отвечать
Ну а теперь я перейду к ответу на тот пост
Определяем скорость и высоту падения из поста
Перед тем, как приступлю к вычислениям, хочу сказать, что событие, безусловно, печальное: родители уже собирались видеть своего ребенка взрослым, да и для пацана близилась взрослая жизнь, универ, тусовки, а тут... Грустно, в общем.
Но начнем наши вычисления. Чтобы приблизительно определить скорость падения, нужно, можно сказать, численно продифференцировать: взять два соседних кадра, посчитать перемещение. Я выбрал следующие два кадра:
На первом кадре проведены следующие построения. Отрезками (белые) проложен рост парня (~135,851 пикселя), желтым отрезком обозначено перемещение (93 пикселя), голубым отрезком проложена длина ступеньки у подъезда (~21,932 пикселя)
Все эти длины мы сейчас свяжем с метрами. Длина ступеньки согласно данным из интернета должна составлять 300 мм, ввиду искажения при съемке возьмем 250 мм, откуда отношение между метрами и пикселями (далее обозначу за k) будет равно 0,011399 м/пикс. Да, значение не совсем точное из-за искажения изображения, но погрешность будет не слишком большая. Также определим k, соотнеся с ростом парня. На глаз рост составляет ~165-170 см, с учетом того, что из-за поворота размер искажается, примем для соотношения рост в 150 см, тогда k = 0,011042 м/пикс. Чтобы повысить точность, будем использовать среднее арифметическое двух полученных значений. Тогда по итогу k = 0,0112205 м/пикс., а перемещение составит ~ 1,044 м. А тогда скорость приближенно равна 31,64 м/с.
Теперь на основе общей формулы из начала поста можем узнать, с какой высоты упал десятиклассник. Установившаяся скорость свободного падения по данным из интернета составляет около 55 м/с. Тогда несложно вычислить c для общей формулы:
Подставляя скорость, коэффициент сопротивления и ускорение свободного падения, получим высоту в 70 м, что составляет ~25 этажей (округление в меньшую сторону). Число этажей выглядит довольно значительным, и, вероятно, является слегка завышенным, так как выведенная формула требует постоянства коэффициента сопротивления, чего при подобном падении достичь невозможно. Ну и также 55 м/с (предельная скорость) - это для падения "плашмя", на фото человек летит не так. Скинув в 2,5 раза (цифра примерная и на глаз исходя из изменения миделевого сечения при падении боком)) коэффициент сопротивления получим 54,7 м или 20 этажей. Возможно, цифра еще меньше, но тут я упираюсь в погрешность при подсчете скорости и в собственные (масса, коэффициент сопротивления, площадь миделя) характеристики падавшего, поэтому более точные данные дадут уже только сотрудники органов
На этом пост уже точно заканчивается. Понимаю, что строить научпоп с расчетами вокруг жести не очень хорошее занятие, но надеюсь, что пост не вызовет негатива от читателей. Всем добра, и поменьше бы таких случаев, а в идеале вообще 0
Наглядная экономика
Имея некоторую дисперсию опоздания на работу - имею наглядную модель поведения переходных баянистов: они дифференцируют трёхмерный поток денежной масса и меняют переходы наблюдая экстремумы.
Для дифференцирования трехмерного потока денежной массы, мы можем использовать оператор набла ₽
Пусть у нас есть трёхмерный поток плотности массы, заданный в виде векторной функции:
ρ(r, t) = ρx(x, y, z, t) i + ρy(x, y, z, t) j + ρz(x, y, z, t) k,
r = (x, y, z) - трехмерный вектор позиции
t - время
Тогда дифференцирование такого потока будет выглядеть следующим образом:
€ρ = (∂/∂x)ρx i + (∂/∂y)ρy j + (∂/∂z)ρz k + (∂/∂t)ρx i + (∂/∂t)ρy j + (∂/∂t)ρz k
Оператор набла ₽ выполняет дифференцирование по каждой переменной (x, y, z, t) отдельно
Полученные производные представляют собой скорость изменения плотности денежной массы в каждом направлении и скорость изменения плотности денежной массы с течением времени.
Расчётливые бабки переходов и инфляция ранней вселенной пенсии.
Как выглядит орбита спутника под землей?
Всем доброго времени суток
Когда речь заходит об орбитах и спутниках, мы заранее предполагаем, что они движутся над поверхностью планеты, что логично: целым пролететь сквозь землю он не может. Но. Что если предположить, что может. Допустим, люди придумали такой материал, что он может без какого-либо сопротивления проходить сквозь другие тела. И сделали из него спутник. И запустили на орбиту. Как будет выглядеть такая орбита? В этом сейчас и будем разбираться
Почему орбиты под землей и над землей отличаются
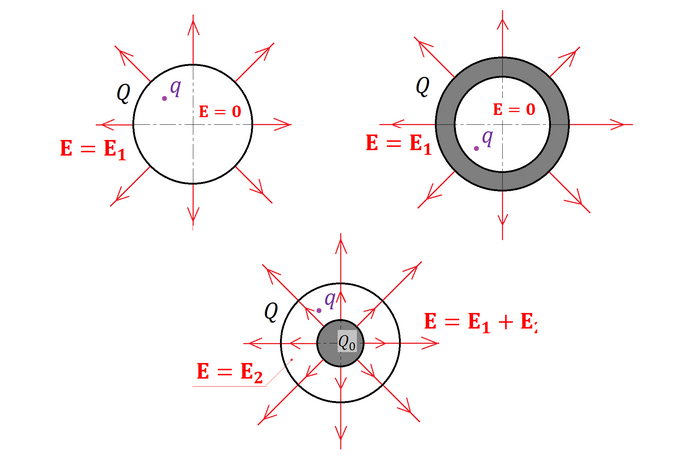
Чтобы разобраться, почему орбиты будут отличаться, зайдем немного издалека и вспомним электродинамику. В школьном курсе физики рассказывают, что если равномерно нанести заряд на сферу, то электрическое поле будет только снаружи сферы, но не внутри. Более наглядно это показано на картинке:
Видно, что электрическое поле есть только вне сферы. Еще на 3 картинке показано, что если есть 2 сферы, то под большей поле будет создавать только меньшая. Если поместить под сферы заряд q << Q (значительно меньший, чем заряд сферы), сферы на заряд действовать не будут (кроме малого шара на 3 картинке)
А теперь представим, что какой-то пробный заряд движется внутри заряженного шара. По его объему заряд распределен так, что его плотность зависит только от расстояния от центра (то есть, отступая от центра шара на одинаковые расстояния в 2 случайных направлениях, мы придем в точки с одинаковым зарядом). Как определить, с какой силой такой шар действует на заряд? Думаю уже все догадались: нужно шар разбить на шар поменбше и толстостенную сферу побольше, да так, что бы пробный заряд был над первым, но под второй:
Зазор на 2 картинке представлен для наглядности, в действительности он бесконечно мал
В данном случае у нас также на заряд действует только шар поменбше, а вот внешняя сфера заряд никак не трогает. Соответственно, если сместим заряд внутри сферы, то как бы изменим заряд того тела, что действует на нашу частичку q (естественно в самой сфере ничего не меняется, меняются заряды только в уравнениях движения)
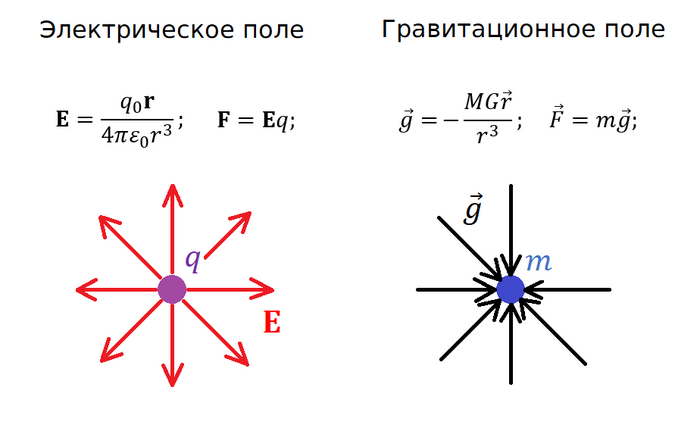
Но что это мы все про заряды да про заряды? Зачем они нам, если мы на орбиты и гравитацию смотреть собрались? А вот зачем. Взгляните на формулы для полей и сил электрического и гравитационного взаимодействия:
Формулы по сути отличаются только буквами (ну и еще минус у гравитации), а значит то, что я только что рассказывал про заряды, работает и для гравитации. То есть на спутник, летящий под землей, будет действовать только та часть планеты, которая находится под ним, как это было с зарядом в сфере (планеты, в данном случае Земля, принимаются сферическими). Ну а значит теперь мы знаем, в чем отличие движений под и над землей, и можем составлять уравнения движения
Но перед этим оставлю небольшое дополнение для самых диких математиков тех, кому интересно, почему все-таки под сферой поля нет
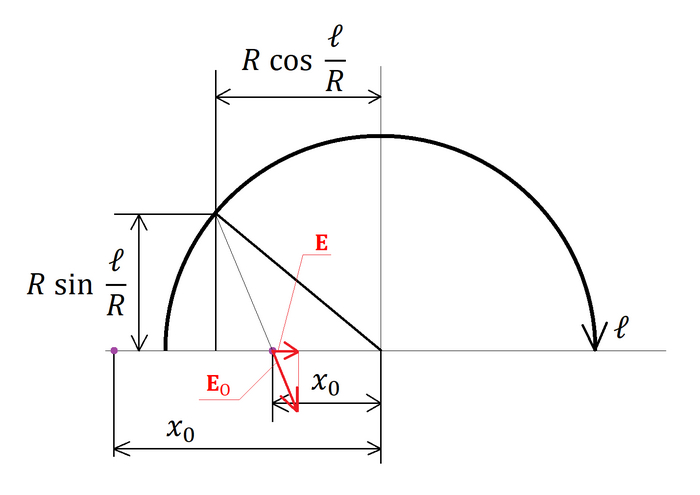
Проведем систему координат с нулем в центре сферы. Проведем кривую ось l вдоль сферы так, чтобы она лежала в плоскости xOy. Будем рассматривать поле в точке, смещенной из нуля по оси Ox (смещение по всем 3 осям равнозначно смещению по одной из осей, просто значения координат поменяются). Вернее, проекцию поля на ось Ox, по другим направлениям (перпендикулярно Ox) поля, очевидно, нет в силу симметрии:
Вдоль оси l разбиваем сферу на множество колец толщиной dl, выражаем заряд dq на кольцах, затем поле dE каждого из колец, суммируем, короче, все тривиально:
Итак, поле есть только вне сферы. Если построить график проекции поля, то может показаться что само поле отрицательно, но это не так, просто проекции получились на ось, противоположно направленную оси Ox
Уравнения движения
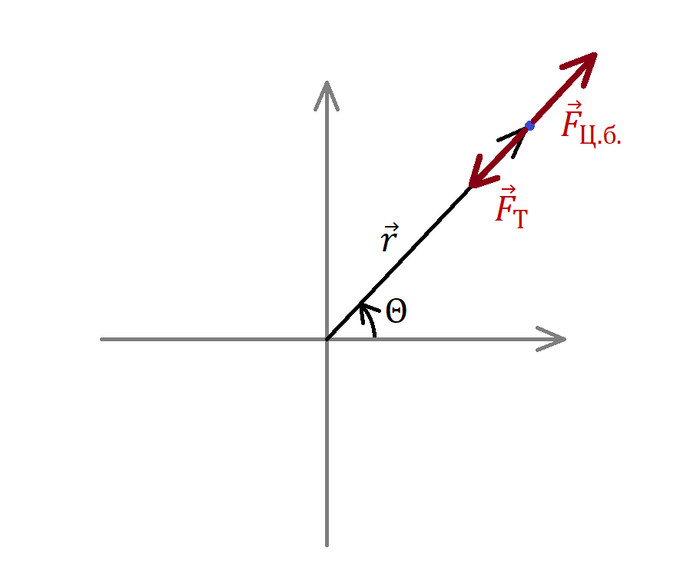
Движение будем рассматривать в полярной системе координат, ибо так удобнее, а силами сопротивления будем пренебрегать, все-таки спутник у нас сквозь всего проходит. Вдоль радиуса (от центра Земли до спутника) будут действовать только 2 силы: сила тяжести и центробежная сила:
Записать уравнение движения для этого направления несложно, обычный 2 закон Ньютона. Лучше разберемся, как записать уравнение для угла и угловой скорости. И сделать это проще всего через закон сохранения момента импульса (момент импульса - мера вращательного движения, то есть тот же привычный импульс p = m * v, только для вращения). Записываем, дифференцируем и компонуем оба уравнения (для радиуса и для угла) в одну систему
Вот уравнения и готовы. Почти. В первом выражении у нас осталась не определена функция массы планеты от расстояния до ее центра. Массы, которая притягивает, а не всей массы планеты, разумеется. И определим мы ее 2 разными способами
Орбиты при постоянной плотности Земли
Начнем с чего-нибудь попроще. Представим, что плотность постоянна, тогда масса будет иметь самый простецкий вид: объем шара некоторого радиуса умножить на плотность. Запишем уравнения в такой форме и попробуем ручками решить эту систему:
Иии... В поиске аналитического решения меня поджидало фиаско. Сколько я ни пытался придумать подстановки, ничего толкового не выходило. Собственно, те преобразования, которые вы видите - замена переменных: теперь мы ищем, как радиус зависит от текущего угла. Однако здесь нас поджидает нелинейный диффур, который браться не очень хочет. К слову, если забить уравнение в Wolfram, то он таки его решит, вернее из дифференциального сделает обычным. Вот только то обычное уравнение не имеет аналитического решения, а значит и диффур тоже. Жаль, а ведь можно было бы и новые законы Кеплера придумать :)
Но да ладно, еще раз запишем уравнения, только теперь сделаем M кусочно-заданной, ну то бишь с какого-то радиуса будем делать ее константой. Это добавит в модель поверхность Земли, и по итогу орбита спутника сможет проходить и под и над Землей:
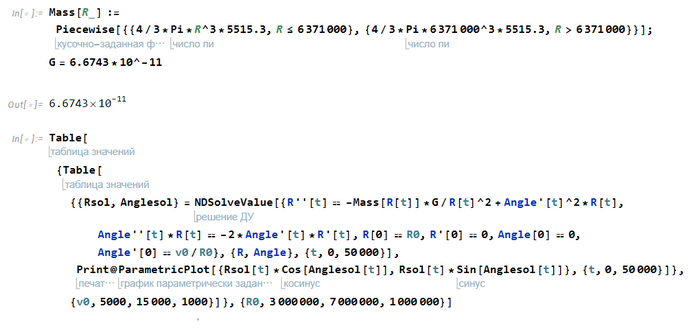
Теперь запишем это все на языке Wolfram-а, смоделируем несколько траекторий...
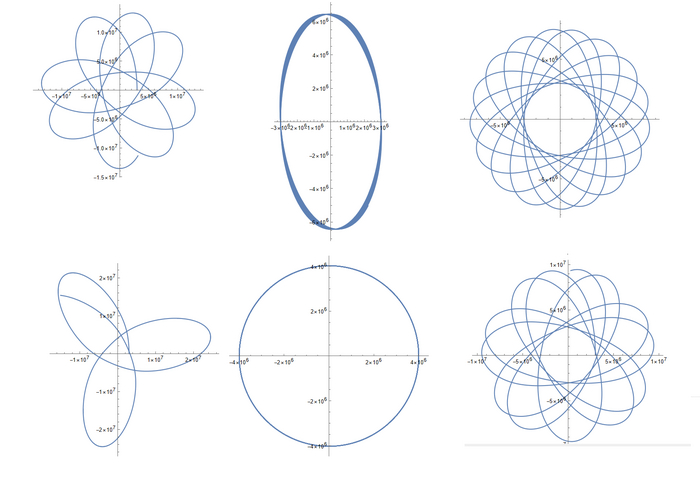
... и получим вот такие довольно красивые графики
Честно говоря, не ожидал, что спутник будет лететь по столь интересным траекториям. Но да ладно, их вы и сами посмотреть можете, а я лучше расскажу, как они устроены.
Если спутник летит полностью под землей, то его траектория - эллипс, центр которого совпадает с центром Земли
Если же спутник движется и под и над поверхностью планеты, то его траектория чередуется из эллипсов (под - эллипс с центром в центре Земли, над - эллипс с центром Земли в фокусе). Но упрощенно ее можно представить так: берем один из вариантов траектории и с каждым витком поворачиваем траекторию на какой-то угол. Если в основном спутник летит под землей, то выбираем траекторию подземного спутника и постоянно ее вращаем. Если в основном над землей - вращаем траекторию надземного спутника. Чем-то похоже на очень сильную прецессию перицентра, хотя, конечно, прецессия исходит из теории относительности, а не из подземных полетов :)
Орбиты с реальной плотностью Земли
Естественно в действительности плотность Земли меняется с глубиной. И это тоже нужно учесть
Первым делом запишем уравнения движения, они по сути такие же, только формула массы другая:
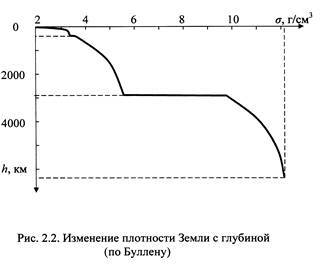
Ну что ж, теперь нужно найти график плотности. В интернете мне удалось найти только одно изображение, где показан график зависимости плотности от глубины, им и будем пользоваться
Выбрав несколько точек с каждого гладкого участка, мы можем при помощи интерполяции сделать похожую на каждый из участков функцию. Затем соединяя отдельные участки в кусочно-заданную функцию получим полноценную функцию плотности, из которой интегрированием можно получить функцию массы. Ну значит запускаем Wolfram и вперед... А нет! Если мы просто проинтегрируем, то Wolfram будет жутко тормозить. Поэтому посчитаем массу Земли при конкретных значениях радиуса и из них, опять-таки интерполяцией, сделаем функцию массы. Я решил взять 27 точек, так как число 6371 делится нацело на 27 (Радиус Земли составляет 6371 км):
Код, вычисляющий точки для дальнейшей интерполяции
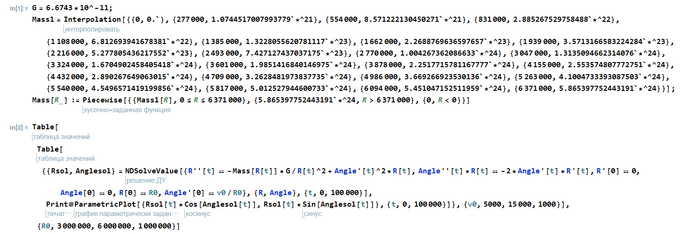
Теперь запишем другой код. В нем как раз мы будем интерполировать массу, а также в нем запустим расчет и выведение траекторий:
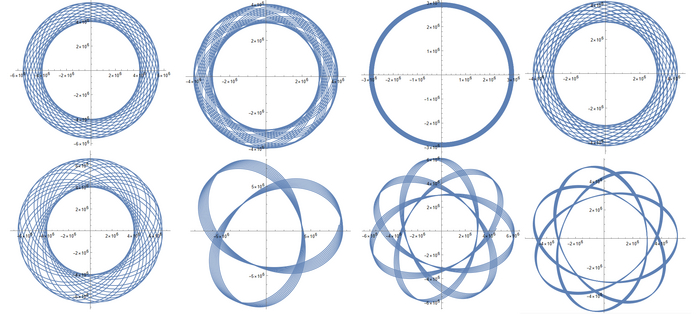
И получим... Еще более красивые графики:
И да, это все траектории, а не просто придуманные красивые графики. Код я написал так, что Wolfram считает первые 100 000 секунд полета, за которые спутник успевает сделать много витков. Вот и получаются такие красивые колечки или просто симметричные узоры. К слову, есть и графики, похожие на случай с постоянной плотностью:
В случае с переменной плотностью траектория остается похожей на эллипс, но теперь он вращается вообще всегда. К слову, можно также заметить, что если спутник движется в основном под землей, то центр Земли находится рядом с центром эллипса, а если над землей - рядом с фокусом эллипса
Есть, конечно, и привычные траектории вроде гипербол, которые получаются, если спутник двигался слишком быстро:
Как самому строить такие траектории
Полагаю, такие красивые графики могут вызвать желание самому их построить, попробовать разные параметры орбит и прочего. И на этот случай я решил оставить код для Wolfram Mathematica, при помощи которого вы сможете сами позапускать спутники под землю. На компьютере, естественно :). Ctrl + C, Ctrl + V, ну и подставить нужные вам цифры:
Для постоянной плотности:
Запустить 1 раз, перед построением графиков: Mass[R_] :=Piecewise[{{4/3*Pi*R^3*5515.3,
R <= 6371000}, {4/3*Pi*6371000^3*5515.3, R > 6371000}}]; G =
6.6743*10^-11
Для построения графика запускаете этот код: v0 = 5000; R0 = 3000000; t0 = 100000; {Rsol, Anglesol} =NDSolveValue[{R''[t] == -Mass[R[t]]*G/R[t]^2 + Angle'[t]^2*R[t],
Angle''[t]*R[t] == -2*Angle'[t]*R'[t], R[0] == R0, R'[0] == 0,
Angle[0] == 0, Angle'[0] == v0/R0}, {R, Angle}, {t, 0,
t0}]; ParametricPlot[{Rsol[t]*Cos[Anglesol[t]],
Rsol[t]*Sin[Anglesol[t]]}, {t, 0, t0}]
Для реальной плотности:
Запустить 1 раз, перед построением графиков: G = 6.6743*10^-11; Mass1 =Interpolation[{{0, 0.`}, {277000, 1.0744517007993779`*^21}, {554000,
8.571222130450271`*^21}, {831000,
2.885267529758488`*^22}, {1108000,
6.812693941678381`*^22}, {1385000,
1.3228055620781117`*^23}, {1662000,
2.2688769636597657`*^23}, {1939000,
3.5713166583224284`*^23}, {2216000,
5.277805436217552`*^23}, {2493000,
7.427127437037175`*^23}, {2770000,
1.004267362086633`*^24}, {3047000,
1.3135094662314076`*^24}, {3324000,
1.6704902458405418`*^24}, {3601000,
1.9851416840146975`*^24}, {3878000,
2.2517715781167777`*^24}, {4155000,
2.553574807772751`*^24}, {4432000,
2.890267649063015`*^24}, {4709000,
3.2628481973837735`*^24}, {4986000,
3.669266923530136`*^24}, {5263000,
4.1004733393087503`*^24}, {5540000,
4.5496571419199856`*^24}, {5817000,
5.012527944600733`*^24}, {6094000,
5.451047152511959`*^24}, {6371000, 5.865397752443191`*^24}}];
Mass[R_] :=
Piecewise[{{Mass1[R], 0 <= R <= 6371000}, {5.865397752443191`*^24,
R > 6371000}, {0, R < 0}}]
Для построения графика запускаете этот код:v0 = 5000; R0 = 3000000; t0 = 100000; {Rsol, Anglesol} =NDSolveValue[{R''[t] == -Mass[R[t]]*G/R[t]^2 + Angle'[t]^2*R[t],
Angle''[t]*R[t] == -2*Angle'[t]*R'[t], R'[0] == 0, Angle[0] == 0,
R[0] == R0, Angle'[0] == v0/R0}, {R, Angle}, {t, 0,
t0}]; ParametricPlot[{Rsol[t]*Cos[Anglesol[t]],
Rsol[t]*Sin[Anglesol[t]]}, {t, 0, t0}]
Первые 3 переменные (v0, R0 и t0) задаете сами, это начальная скорость (м/с), начальное расстояние от центра Земли (м) и время (с), до которого будет рассчитана траектория соответственно, изначально там будут указаны стартовые значения. Также сразу предупрежу: весь код для одного случая (например, код для постоянной плотности) нужно писать в одном файле, но в этот же файл нельзя писать код для другого случая (для переменной плотности)
Что-то похожее на заключение
На это пост заканчивается. Надеюсь, материал был понятен и интересен... ну или графики хотя бы глаз порадовали) Если есть вопросы - пишите в комментариях, будем разбираться
Всем добра и побольше аналитических решений)
Дифф. уравнение в Maple
Добрый день! Возможно, кто-то работает в Maple или понимает его лучше (гораздо лучше) меня.
Мне нужно решить дифф. уравнение в аналитическом виде. alpha и gamma – коэффициенты (можно обозначить и иначе).
При попытке записать уравнение в переменную получается ошибка: Error, invalid derivative
Поскольку мне ни разу не приходилось решать такие уравнения даже в Maple, я не могу разобраться, что здесь не так.
Уравнение является уравнением гармонического осциллятора (по какой причине следует построить и соответствующий plot).
Буду благодарен за любую содержательную помощь. Спасибо!
Как выйти на орбиту при помощи пушки
Всем доброго времени суток. Чуть менее года назад мне попался пост про SpinLaunch, где в комментариях речь зашла о том, можно ли выйти на орбиту при помощи пушки и без включения двигателей. Ну и мне захотелось узнать ответ на этот вопрос. Захотелось, но то времени не было, то просто лень было что-то делать. Но вот руки дошли до поста, поэтому прямо сейчас проверим, можно ли выйти при помощи пушки на орбиту? А также в конце затрону вопрос о том, как лучше всего выходить на орбиту с использованием и пушки, и двигателей
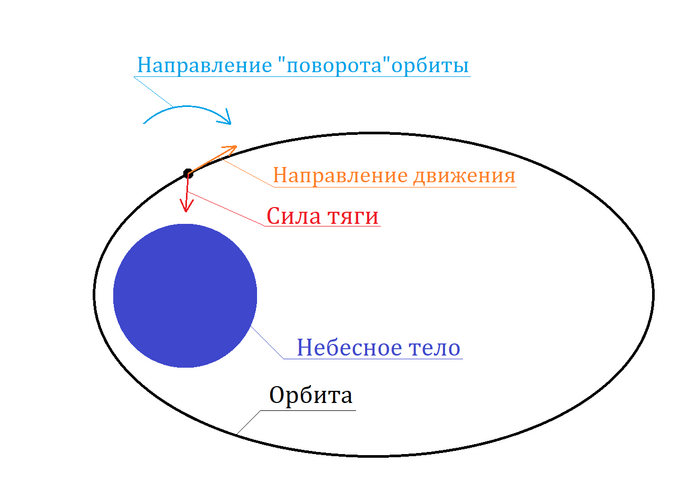
На первый взгляд кажется, что выйти на орбиту, придав спутнику импульс на поверхности планеты, невозможно. Если не учитывать сопротивление воздуха, то точка старта будет принадлежать орбите аппарата, а еще там вертикальная скорость будет положительна, из чего следует, что перицентр окажется ниже поверхности. Но вот если добавить атмосферу, то картина изменится. Спутник всегда будет двигаться только вверх в атмосфере (ему все-таки из нее выбраться надо). Поэтому аэродинамическое сопротивление будет толкать спутник вниз. Если вы знакомы с орбитальной механикой и/или играли в Kerbal Space Program, то, я уверен, знаете, что если включить двигатель по направлению к или от небесного тела, то орбита начнет как бы "поворачиваться" относительно положения аппарата. Более понятно это показано на картинке, где орбита будет отчасти похожа на текущую орбиту нашего спутника в какой-то момент времени при движении в атмосфере:
Можно сразу заметить, что при таком "повороте" орбиты перицентр увеличивается. Значит теоретически может быть такой случай, когда спутник сам выйдет на орбиту. Давайте это проверим и попытаемся найти такой случай
Модель спутника
Так как основы никакой нет, то сами выберем, каким будет спутник. В качестве модели я решил взять конус диаметром 1 м, углом раствора 30 градусов и массой 500 кг. Этакий набор кубсатов под бронированным колпаком :)
В полете важную роль будет играть сопротивление воздуха, поэтому вычислим среднее значение коэффициента сопротивления воздуха. Но не совсем того, что нам дает классическая формула F = p * S * c * v^2 / 2, а немного другого. Запишем формулу ускорения от аэродинамического сопротивления: a = p * S * c * v^2 / 2m, заметим, что все, кроме p и v, - это константы. p, то есть плотность среды, мы заменим на p0 * e^(k * H), то есть аппроксимируем плотность от высоты при помощи экспоненты. Перепишем формулу ускорения: a = (p0 * S * c /2m) * v^2 * e^(k * H). Теперь все константы перепишем в одну a = C * v^2 * e^(k * H). Вот эту C мы и найдем
Сама по себе C - это не константа, так как коэффициент сопротивления воздуха для одной и той же формы разный при разных скоростях. Однако на больших скоростях он колеблется незначительно (что мы дальше и увидим), поэтому его можно принять константой (в целом, для более точного решения нужно C найти через интерполяцию его значений при конкретных скоростях, но для этого нужно взять довольно много точек, что делать не особо хочется, да и на точность это сильно не повлияет, зато прибавит лишней работы)
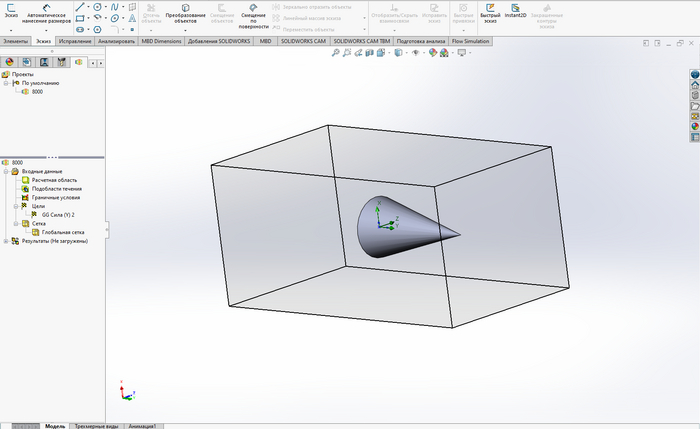
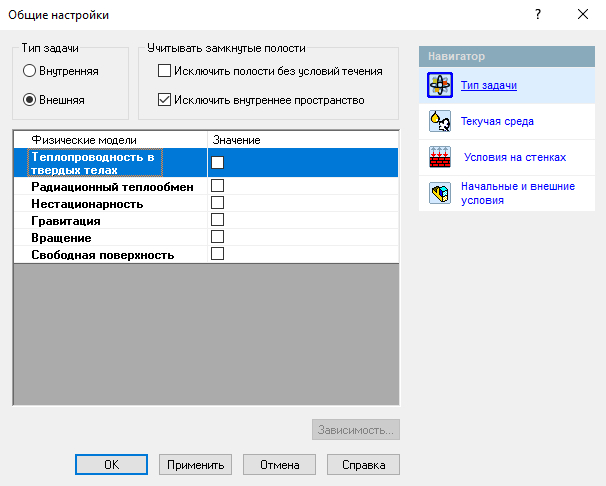
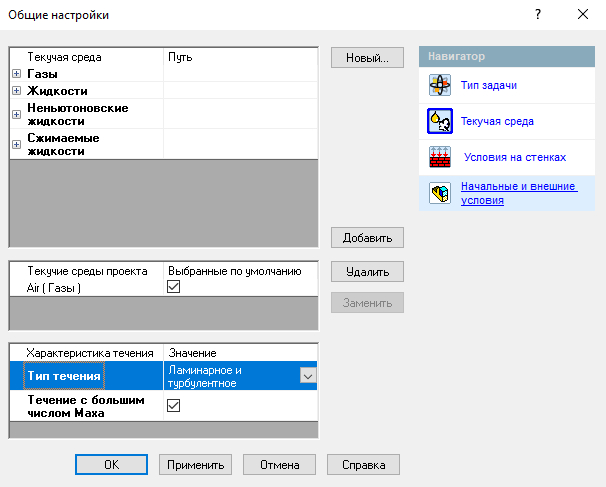
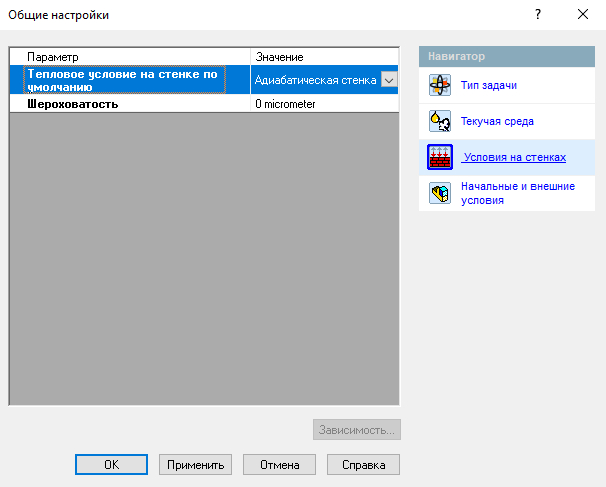
Ну коль надо измерять сопротивление воздуха, то нам понадобится САПР, в моем случае это SolidWorks. Запускаем, создаем модель, заходим во FlowSimulation и создаем проект:
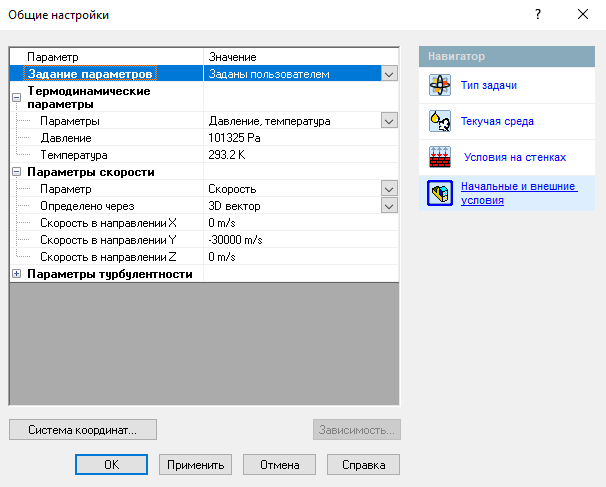
Скорость -30000 м/с - один из расчетных случаев
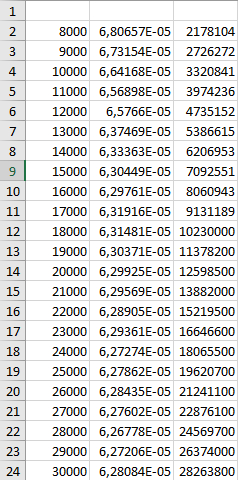
Теперь поставим в проекте цель находить силу по оси Oy и по несколько раз запустим расчет, каждый раз меняя значение скорости потока воздуха. Я буду измерять с 8000 м/с до 30000 м/с с шагом в 1000 м/с. Для каждой скорости записываем действующую силу. Дальше, возвращаясь к формуле ускорения, мы избавимся от e^(k * H). Так как в SolidWorks-е воздух имеет такую же плотность, что и воздух у поверхности Земли при н.у., то переменная H становится равна нулю, а экспонента - единице. Ну а чтобы вычислить тот самый коэффициент, мы будем силу делить на массу и на квадрат скорости (сила на массу даст ускорение, а если ускорение поделить на квадрат скорости, то получим только коэффициент, ну и еще экспоненту, но мы от нее избавились). Короче говоря, пишем таблицу в экселе:
1-ый столбец - скорость, 2-ой - искомый коэффициент, 3-ий - сила, действующая на модель при данной скорости
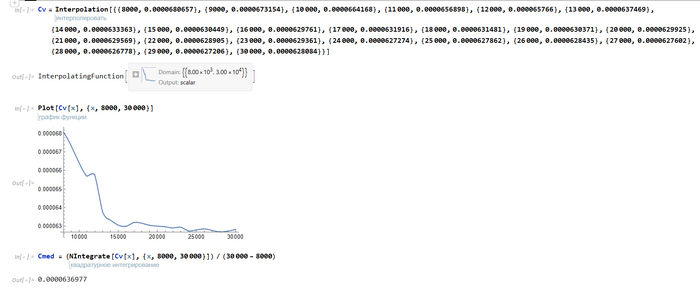
Осталось найти среднее значение. Но как это сделать? Будем действовать так же, как при нахождении средней скорости: проинтегрируем функцию C(v), полученную интерполяцией табличных значений, а затем разделим на разность пределов интегрирования. В качестве пределов интегрирования будут использованы минимальная и максимальная скорость, что логично. Запускаем Wolfram Mathematica, пишем и выполняем следующий код:
Можно заметить, что сам коэффициент колеблется незначительно, что нам на руку
В целом, это все, что нужно знать про модель. В решении мы пренебрежем уменьшением массы от испарения аблятора, напряжения и деформацию рассматривать не будем (так как первое нам не нужно, а второе будет очень маленьким). Также примем, что наш конус при движении острием вперед устойчив, то есть его ось всегда совпадает с вектором скорости воздуха. На деле так случается не всегда, все зависит от центра масс, но будем считать, что спутник мы сделали устойчивым
Плотность атмосферы
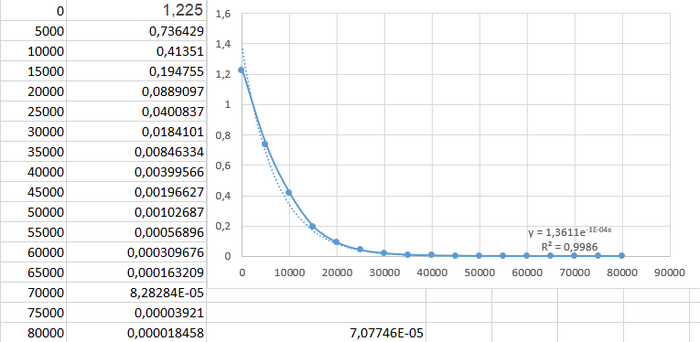
У нас остался неизвестный коэффициент при экспоненте, его тоже надо найти (конечно, можно и плотность интерполировать, но для этого нужно много точек при больших высотах, что, опять же, делать не очень приятно, к тому же приближение через экспоненту работает довольно точно). Находим ГОСТ 4401-81 Атмосфера стандартная и из него берем плотности воздуха при разных высотах, далее записываем их в эксель и строим график. Создаем линию тренда, делаем ее экспоненциальной и выводим уравнение на график
Тут же сразу замечаем, что у полученной функции в нуле плотность не равна плотности воздуха при нулевой высоте. Поэтому полученный прежде коэффициент для сопротивления воздуха нужно переделать. В нем есть начальная плотность, которая как раз равна 1,225 кг/м^3. А при приближении экспонентой она должна быть равна 1,3611 кг/м^3. Поэтому сам коэффициент разделим на 1,225 и домножим на 1,3611. На картинке он есть, вон в низу красуется)
Составление модели полета
Вводные данные есть - значит можем приступать к самой модели полета. Сразу определимся, что в ней будем учитывать, а что не будем. Во-первых, в учет пойдут только сила тяжести и сила сопротивления воздуха. Остальные силы очень малы, поэтому ими можно пренебречь. Помимо этого не будем учитывать моменты. Мы заранее приняли, что аппарат будет устойчив, поэтому можно не записывать уравнения моментов и не вводить зависимость сопротивления воздуха от ориентации: спутник всегда направлен по движению (a.k.a. по програду). Также по мелочи, не будем учитывать изменение радиуса Земли (и эллиптичность самой Земли в сечении) при разной широте старта
Систему координат возьмем декартову, трехмерную. Нуль координат будет совпадать с центром Земли
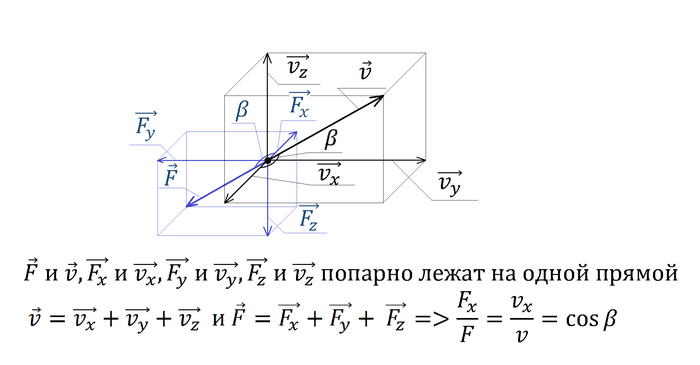
Приступим к формулам. Нам надо выразить ускорения по 3 осям
Начнем с силы тяжести. При помощи чертежа находим, как будет зависеть проекция силы на ось от координат тела:
Выражение записано только для оси Ox, однако оно аналогично для и для Oy и Oz
Теперь выражаем F, вернее a, и записываем проекции ускорения от силы тяжести на каждую из осей
Теперь строим чертеж для силы сопротивления воздуха:
И также выражаем ускорение от АС, а затем и ускорение в проекциях
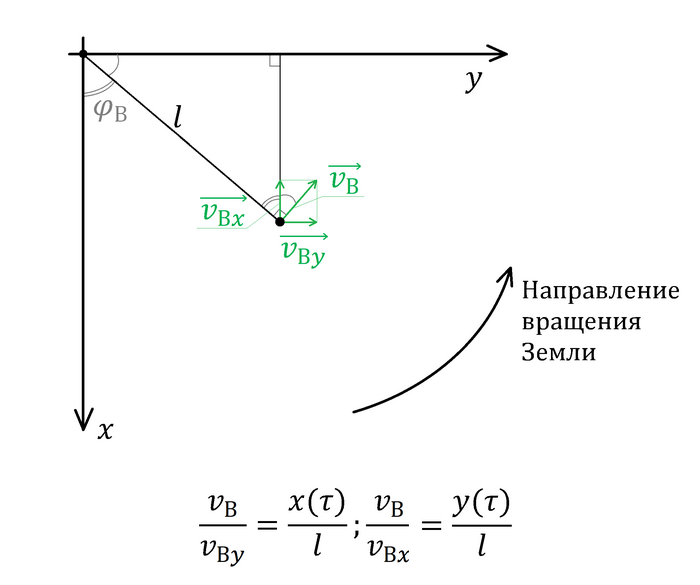
Однако здесь можно сразу заметить один нюанс: мы не все выразили через x, y и z и их производные. Дело в том, что Земля крутится, а вместе с ней и атмосфера. При помощи чертежа определим, как зависит скорость воздуха от координат и перезапишем v-шки через них:
Перезапишем формулы для сопротивления воздуха:
И составим сами уравнения модели:
Казалось бы все, модель готова. Но тут есть нюанс. Работать с трехмерной моделью полета не очень удобно, к тому же это более ресурсозатратно (а еще у меня Wolfram может сильно косячить с графиками в 3D). Поэтому сократим количество измерений до 2
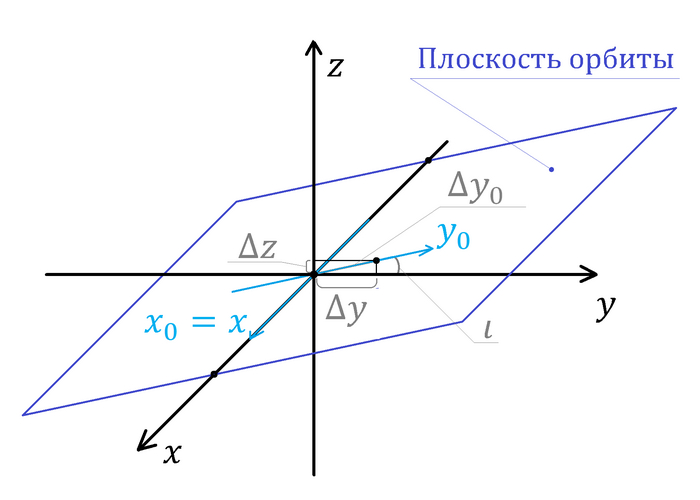
Для этого примем, что орбита находится в одной плоскости (на деле она чуть-чуть смещается, как раз из-за вращения атмосферы, но это смещение довольно мало). Плоскость орбиты должна проходить через место старта и нуль системы координат. Из этого следует, что ее наклон к плоскости Oxy равен широте места старта. Теперь для удобства примем, что ось Ox принадлежит этой плоскости (это соответствует случаю, когда x-координата места старта равна нулю). Теперь на этой плоскости проведем систему координат Ox0y0, причем x0 совпадает с x (поэтому вместо x0 будем писать просто x). Построим чертеж и выразим y и z через y0, а также запишем их производные первого и второго порядка:
Перепишем систему в двух измерениях. y0 выразим из y (выражение через z и y дают разные формулы, которые численно не сильно отличаются. Это как раз из-за того, что на деле орбита не находится в одной плоскости):
Вот теперь модель готова
Поиск решений для задачи
Теперь надо найти такие комбинации начальных скоростей по обеим осям, чтобы аппарат вышел на орбиту (или убедиться, что их нет). Так как данная модель не имеет аналитического решения, то придется просто перебирать решения (сразу добавлю, что для всех параметров сразу все же можно найти решение, для этого нужно решить систему R(t0) = (6371000 + 180000) м) и R'(t0) = 0 (здесь вводится полярная система координат), однако я не нашел способа сделать это в Wolfram-е, а также для такого решения банально не хватает мощностей моего компьютера). Это не даст стопроцентный ответ на поставленный в начале вопрос, но по самим траекториям можно будет предположить, каков ответ
Как будем перебирать? Я решил выбрать более менее подходящий вариант между точностью и затратами на расчет, поэтому выбрал ограничения для начальных горизонтальной и вертикальной скоростей в 3000 м/с и 8000 м/с соответственно снизу и 30000 м/с сверху (да, стоило в начале посчитать коэффициент вплоть до 30000*Sqrt(2) м/с, но коэффициент ведь считаем постоянным, а поэтому можно использовать и тот, что есть). Шаг для обеих скоростей выберу в 500 м/с. В итоге получим 2475 траекторий, которые надо отсмотреть и проанализировать
Также в решении надо будет ввести ограничение по времени внутри системы (то есть от какого до какого момента моделировать полет). Для этого нижнее (оно же начальное) значение времени будет равно 0, а верхнее я решил принять равным орбитальному периоду для спутника на эллиптической орбите с апогеем ровно на границе сферы тяготения и перигеем в 180 км (число взято не совсем из головы, изначально я предполагал вводить уплощенную модель, которая имеет аналитическое решение, чтобы определить, среди каких скоростей искать решение, и вот там как раз спутник должен был выйти на орбиту с перигеем в 180 км. Но решение этой модели давало вообще неправильные цифры (для примера - чтоб хотя бы просто не упасть на Землю, нужна была горизонтальная скорость в ~150 км/с, что в полной модели давало достижение второй космической), поэтому я от него отказался)
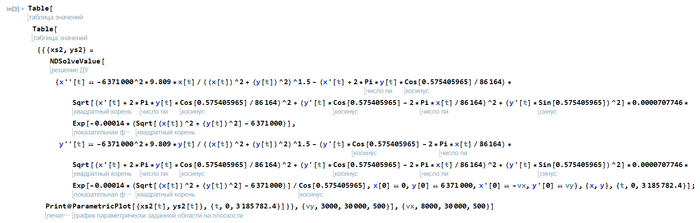
Итак, пишем код, запускаем его и идем пить чай, че еще делать то)
Через несколько минут приходим назад и мотаем вниз в поиске кучи надписей Null в фигурных скобочках. Если они есть и новых графиков не появляется, значит расчет окончен. Можем приступать к анализу
Но перед этим сразу определим, какие графики мы можем теоретически получить. Их 4 типа:
Прямая с малой кривизной. На координатных осях значения до примерно 1*10^11. Это случай, когда аппарат набрал вторую космическую скорость и покинул сферу тяготения Земли
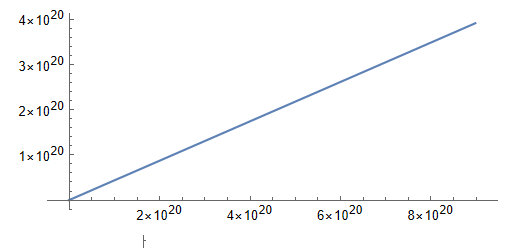
Прямая с малой кривизной. На координатных осях очень большие значения, больше чем в первом типе. Это случай когда спутник упал на Землю. Из-за экспоненциальности плотности воздуха и учета вращения атмосферы спутник, оказавшись под поверхностью планеты, начинает испытывать очень сильное действие силы сопротивления воздуха, которое не останавливает его, а заставляет двигаться. В купе с этим из-за перехода к 2 измерениям спутник не движется по "орбите" под землей, а очень сильно ускоряется крутящейся атмосферой, из-за чего набирает гигантскую скорость и улетает от Земли на миллионы световых лет
Разомкнутый эллипс. Это тот случай, когда апогей оказался не сильно выше границы сферы тяготения. Так как есть ограничение по времени, заданное максимально высокой орбитой, то при апогее ниже границы, эллипс должен быть замкнутым (или почти замкнутым, но там расстояние между началом и концом кривых должно быть маленьким)
Замкнутый эллипс. Это как раз стабильная орбита. Эллипс может быть чуть-чуть разомкнутым, об этом написал выше
И теперь скроллим все две с половиной тысяч графиков и смотрим на них. Пока прикреплю пару примеров:
Первый тип траектории
Второй тип траектории. Видны очень большие значения координат на осях
Эллипс, который "не шмог" ) Неизвестно, какой у него перигей, но вот апогей оказался выше границы сферы тяготения, поэтому на такую траекторию в реальности все же не выйти. Ах да, это третий тип
Еще один довольно причудливый график. Здесь спутник вышел из атмосферы, сделал виток и упал на Землю (об этом говорит последний кусок траектории), после чего полетел далеко-далеко от Земли. Ну и это второй тип траектории
Как вы могли заметить, я не привел пример 4 типа графиков. А все потому что таковых не было. Хоть выборка и довольно грубая (шаг аж в 500 м/с), она дает понять, что скорее всего выйти на орбиту без включения двигателей не получится (на самом деле то довольно много есть итераций, в которых спутник покинул атмосферу, но потом упал на Землю). Что ж, удручающе, хотелось найти какое-нибудь решение. Хоть и такой результат неудивителен
Как все же можно выйти на орбиту?
Но представим, что нам ну очень хочется на орбиту. Мы уже и пушку купили, и спутник. Логичным становится то, что к спутнику нужно приделать ступень. Представили, что приделали, теперь надо узнать, как из пушки нужно выстрелить и сколько надо дельты
Пусть мы хотим выйти на круговую орбиту радиусом R + R0. Если в описанной прежде системе закрепить угол наклона к горизонту и менять только скорость, то можно заметить, что при росте скорости растет апогей (ну то есть высота апогея от скорости - функция монотонная). А значит, для данного угла существует только одно значение скорости, которому соответствует требуемое значение апогея. Тогда общее множество решений для случая, когда апогей равен R, является некоторой кривой (при решении R(t) = R + R0 это будет поверхность t(v0, a), и это будут все траектории, проходящие через R + R0. Так как при увеличении скорости растет апогей, то нам для каждого угла a нужна одна скорость, которая будет минимальна для этого угла a в t(v0, a). А это как раз и получается кривая)
Теперь из этого множества решений нужно взять одно подходящее. И оно соответствует той комбинации угла наклона и начальной скорости, при которой последняя будет минимальна. Это следует из того, что с ростом скорости максимальное значение силы сопротивления воздуха растет квадратично, а скорость в апогее - приблизительно линейно. В данном случае увеличение скорости незначительно понизит нужную дельту (линейно уменьшится), зато сильно повысит массу конструкции спутника и ступени (будет также увеличиваться квадратично). Учитывая сильный рост массы конструкции, чтоб дельты было достаточно, нужно будет также увеличить начальную массу по сравнению со случаем для минимальной скорости (это следует из того, что нужная дельта убывает медленнее, чем растет масса конструкции). В итоге получим большие затраты по топливу, материалам для ступени, большие ограничения на спутник из-за перегрузок и большие энергозатраты на запуск из пушки. А это нам не особо надо. Конечно, могут быть случаи, когда подходящая начальная скорость не равна минимальной. Но тут уже нужно конкретно рассматривать конкретную ступень и спутник.
Если сократить, то получим, что для выхода на орбиту нужно решить один из вариантов модели полета из поста (в идеале - трехмерную, используя плотность и коэффициент сопротивления воздуха как функции, полученные интерполяцией, а также учитывая все все все силы, испарение аблятора, моменты и т.д.) в параметрическом виде, причем в полярных координатах (перейти к ним не сложно: выражаем декартовы координаты через произведения радиуса и синусов/косинусов угла/углов -, так что это не проблема), далее найти функцию t(v0, a), удовлетворяющую условию R(v0, a)(t) = R + R0, затем найти кривую, в которой каждому a соответствует минимальная v0 и среди v0, принадлежащих этой кривой, найти либо минимальную v0 (то есть минимальную v0 для t(v0, a)), либо найти такую v0, которая даст минимум массы спутника со ступенью (в большинстве случаев она совпадает с минимальной). Затем по v0 найти a, решить модель с заданными параметрами и уже по ней определить все остальные требования к спутнику (дельта, прочностные характеристики и т.п.). Замечу, что процесс итерационный, так как коэффициент сопротивления воздуха берется из модели аппарата, а модель из характеристик, которые берутся из решения модели полета, для которой нужен коэффициент сопротивления воздуха...
Ну а на этом пост заканчивается, ведь ответы на все вопросы из его начала получены. Надеюсь, читать было интересно, а содержание было понятным. Если есть какие-либо вопросы или что-то оказалось непонятным - пишите в комментариях, постараюсь более подробно разобрать. Буду рад критике, советам и дополнениям к содержанию поста.
Всем добра и с прошедшим Новым годом)