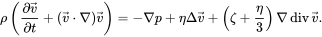Обзорная фотография столбчатых базальтов на северном побережье Ирландии. Лестница гигантов и деталь ее обзорной фотографии

В самых разных уголках нашей планеты встречаются удивительно красивые геологические образования — вертикально стоящие базальтовые столбы в форме плотно прилегающих друг к другу правильных призм, чаще всего шестигранных. Все они в пределах одного базальтового массива имеют одинаковую толщину, обычно от нескольких десятков сантиметров до 2 м, но в разных местонахождениях разную. Наиболее известные столбчатые базальты находятся на севере Ирландии. Это так называемая Тропа гигантов, или Лестница гигантов, — структура, которая образовалась из излившейся лавы в рифтовой зоне при раскрытии Атлантического океана и отделении Ирландии от Британских о-вов, прежде составлявших единое целое. Похожие образования есть и во многих других местах на Земле, например в Исландии, в ущелье Гарни в Армении, на вулканическом острове вблизи побережья Шотландии (знаменитая пещера Фингала), в Неваде и наконец в России (мыс Столбчатый на о. Кунашир).

Рождение формы: пробелы в понимании

Геологов давно занимала загадка происхождения таких правильных форм, но удовлетворительной теории их образования до сих пор предложено не было. Высказывались предположения о генетической связи шестигранных базальтовых столбов с шестиугольными ячейками конвекции Рэлея — Бенара. Эта форма конвекции была открыта в начале прошлого столетия французским физиком Анри Бенаром в эксперименте с тонким горизонтальным слоем вязкой жидкости, подогреваемым снизу (английский физик лорд Рэлей провел теоретический анализ явления). При достижении критического значения температурного градиента весь слой разбивался на одинаковые по размеру шестигранные ячейки, в центре которых жидкость поднималась к свободной поверхности, а по их периферии опускалась вниз. Применительно к базальтам в работе Д. Е. Трапезникова и др. [1] выдвинута контракционно-конвективная модель возникновения столбчатой отдельности, согласно которой в слое жидкой излившейся лавы по мере ее остывания создаются условия для конвекции Рэлея — Бенара. Затем при затвердевании и дальнейшем охлаждении слоя объем массива уменьшается и термические напряжения разрывают его на шестигранные столбы по границам бенаровских ячеек.

Однако эту модель также нельзя признать состоятельной: для наблюдаемой в экспериментах бенаровской конвекции характерны горизонтальные размеры ячеек, примерно равные удвоенной толщине слоя жидкости, тогда как в столбчатых базальтах толщина массива превышает размеры ячеек в десятки раз. Кроме того, неясен механизм связи между конвективными ячейками в базальтовом расплаве и инициацией растрескивания. Если же допустить, что охваченный конвекцией слой намного тоньше излившегося слоя базальта, то непонятно, почему инициированные в нем трещины пронизывают весь массив строго вертикально и столбы до самой подошвы имеют плоские вертикальные грани.

При обзоре чрезвычайно обширной литературы по бенаровской конвекции (см., например, [2]) с удивлением обнаруживаешь, что сама эта теория также полна путаницы и нерешенных проблем. Так, во многих источниках указывается на возможность получения простого точного решения уравнений гидродинамики в приближении Буссинеска (т. е. принимая зависимость плотности от температуры линейной и учитывая изменения плотности только при массовых силах), однако лишь в совершенно абстрактной, физически нереализуемой постановке, когда и верхняя, и нижняя границы являются свободными. Часто упоминается также решение в виде чередующихся цилиндрических валов, вращающихся в противоположных направлениях, однако анализ устойчивости такого решения отсутствует. Но, как справедливо указано в «Гидродинамике» Ландау и Лифшица [3], «осуществляющиеся в природе течения должны не только удовлетворять гидродинамическим уравнениям, но должны еще быть устойчивыми: малые возмущения, раз возникнув, должны затухать со временем». В настоящей статье нас совершенно не интересуют нефизические постановки, нереализуемые граничные или начальные условия, а также нефизические моды потери устойчивости, теоретические мыслимые, но реально не наблюдаемые: и исходные состояния, и способы их модификации должны быть естественными и физически наблюдаемыми.

Невозможно также считать удовлетворительным предложенное И. Пригожиным [4] объяснение геометрии наблюдаемой в экспериментах с тонкими слоями жидкости в прямоугольных кюветах валиковой конвекции трансляцией граничных условий, когда прямолинейная вертикальная стенка как бы распространяется далее по кювете от предыдущего цилиндрического вала к последующему. Ведь валиковая конвекция наблюдается также в чашке Петри или другой круглой посуде, где никаких прямолинейных бортиков нет, причем валы, как правило, подходят к краю кюветы под прямым углом. При этом характерный пространственный период валиковой конвекции может быть в десятки раз меньше диаметра круглой кюветы, так что влиянием боковых границ вдали от них можно смело пренебречь. Валиковая конвекция происходит также в облачном слое атмосферы, порождая часто наблюдаемые протяженные облачные гряды, разделенные равными промежутками (их хорошо видно на фотографии с борта самолета), — а в этом случае никаких твердых границ нет вообще. Наконец, странно было бы для объяснения линейных цилиндрических валов искать одно объяснение, а для шестигранных ячеек Бенара — совсем другое, ни с какими граничными условиями на бортиках не связанное.

Конвективные валы в облачном слое. Вид с самолета

Поэтому попробуем рассмотреть бенаровскую ячеистую конвекцию, исходя непосредственно из соображений устойчивости покоя и устойчивости движения, чтобы понять, какие формы конвекции в этой задаче можно действительно встретить в природе. Начнем с рассмотрения устойчивости тонкого горизонтального слоя вязкой несжимаемой жидкости со свободной верхней границей, с условием прилипания (фиксации) на нижней горизонтальной границе и в приближении отсутствия боковых границ (горизонтальная протяженность слоя настолько больше его толщины, что влиянием боковых границ можно пренебречь). Пусть этот слой покоится, равномерно подогревается снизу, и в нем за счет теплопроводности устанавливается линейный вертикальный градиент температуры и плотности. Теплая, менее плотная жидкость находится ниже более плотной, так что потенциальная неустойчивость налицо. Но сможет ли она реализоваться при любых значениях градиента плотности?

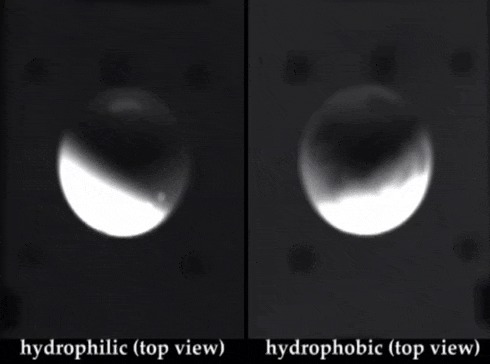
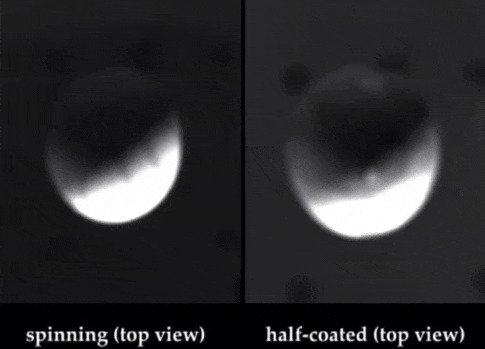
Вихрь из капли

И эксперимент, и теоретический анализ устойчивости позволяют однозначно ответить на этот вопрос отрицательно. Действительно, пусть где-то в объеме жидкости возникла флуктуация плотности / температуры, т. е. некий малый по сравнению с толщиной слоя сферический объем оказался перегретым относительно окружающей его жидкости. (Мы считаем этот объем сферическим, так как уравнение теплопроводности исключает устойчивость иных геометрий возмущений температуры.) Что произойдет с этой теплой каплей дальше? Она начнет всплывать вверх под действием архимедовых сил, подобно аэростату-монгольфьеру. Двигаясь вверх, она попадет в еще более холодный слой жидкости, так что при отсутствии диссипации тепла архимедова сила только увеличится. Но, как мы предположили, жидкость вязкая и теплопроводная, так что всплытию капли будут противодействовать вязкие напряжения, а сама капля начнет остывать и терять плавучесть. И если вертикальный градиент плотности / температуры мал, диссипативные эффекты погасят флуктуацию, она просто рассосется. Итак, существует некое пороговое значение температурного градиента, такое, что малые флуктуации разрастаются, если градиент больше этого значения, и угасают, если он меньше. При этом мы рассматриваем лишь малые флуктуации, порожденные молекулярным хаосом, так как пороговое значение градиента очевидно зависит от масштаба флуктуаций: оно больше для меньших флуктуаций и меньше для больших.

Пороговое значение температурного градиента рассмотрено в [3] и дается формулой

Теперь рассмотрим эволюцию возмущения в случае, когда градиент достаточно велик для разрастания этого возмущения. Силы вязкости жидкости, обтекающей всплывающую каплю, создадут внутри капли нисходящие течения (на ее боковых границах) в системе отсчета, связанной с центром капли, и компенсирующие их восходящие противотечения в ее центре и по оси подъема. Получится тороидальный вихрь.

В результате действия аэродинамических сил капля будет деформироваться: растягиваться в горизонтальной плоскости и сплющиваться по вертикальной оси (по теореме Жуковского аэродинамическая сила ориентирована перпендикулярно направлению движения профиля и пропорциональна циркуляции вектора скорости вокруг профиля). В некоторый момент раскручивающийся тороидальный вихрь создаст гидродинамические силы, достаточные для разрыва сплошности капли, и сплющенная сфера превратится в тор. При этом описанная выше аэродинамическая сила будет продолжать растягивать вращающийся тор по горизонтали и, соответственно, уменьшится малый радиус тора. Окружающая первоначальную каплю жидкость будет силами вязкости вовлечена в оба эти процесса: тороидального вращения относительно кольцевой вихревой линии и вертикального подъема.

Теперь вся эта масса жидкости окажется подверженной действию конвективных сил — подъему по центру и опусканию по периферии возникающей конвективной ячейки. Относительно теплая жидкость будет подсасываться внизу ячейки и подниматься вверх по ее центру, а относительно более холодная опускаться по ее периферии. Архимедовы силы будут способствовать и тому и другому. В тонких слоях рост ячейки будет продолжаться до тех пор, пока ячейка при своем разрастании не коснется дна, где действуют условия прилипания, и некоторое время после этого, пока диссипация энергии вязкими силами у дна не уравновесит ее выигрыш за счет конвекции. На этом дальнейшее разрастание ячейки закончится, и течение внутри ячейки станет стационарным.

Танец в ансамбле

Приведенное рассмотрение, однако, неполно, так как мы пока считали всю окружающую ячейку жидкость покоящейся. Однако на самом деле это не так, и окружающая жидкость также будет вовлекаться в движение вязкими силами. Распространение возмущений приведет к раскрутке рядом с первоначальной ячейкой соседних ячеек, движение жидкости в которых будет согласовано с ее движением в исходной ячейке вследствие условия непрерывности вектора скорости в вязкой жидкости. В принципе возможна (и в некоторых экспериментах действительно наблюдалась) картина течения в виде концентрических кольцевых валов с чередующимся направлением вращения, однако такая конфигурация неустойчива при тех значениях градиента температуры, при которых молекулярных флуктуаций достаточно для инициации конвекции. По-видимому, концентрические конвективные валы можно получить лишь при субкритических для бенаровской конвекции значениях градиента, инициировав конвекцию искусственным созданием сверхкритического возмущения в центре круглой кюветы.

В более реалистичном случае при достижении порогового для ячеистой конвекции значения градиента возникнет множество ячеек, причем раскрутка жидкости по соседству с уже раскрученными ячейками будет облегчена уже наличествующим возмущением. Образуются сначала пары соседних ячеек, которые будут способствовать возникновению третьей и четвертой ячеек рядом с первыми двумя, и так фронт конвекции быстро распространится по всему объему горизонтального слоя. Движение жидкости в каждой такой ячейке можно описать как порожденное находящимся в ее центре вихревым кольцом, а упорядоченный ансамбль таких ячеек — как результат «кристаллизации» вихревых колец, притягивающихся друг к другу, если расстояние между ними слишком велико, и отталкивающихся, если оно слишком мало. В результате достигается наиболее устойчивая структура: гексагональная плотнейшая упаковка, как в монослое одинаковых сферических бусинок на плоскости.

Однако мы пока рассмотрели лишь случай тонкого слоя, когда толщина сопоставима с максимальным размером ячейки, при котором силы вязкости начинают препятствовать дальнейшему разрастанию, или же меньше этого размера. Что произойдет, если этот слой существенно толще? В этом случае мы получим многоярусную ячеистую конвекцию, где над нижним слоем ячеек появится следующий слой, раскрученный в противоположном направлении, т. е. с ячейками, в которых опускание происходит по центру, а подъем — по периферии. В принципе вся описанная выше для монослоя конвективных ячеек картина сохраняется с точностью до обращения векторов скорости, если мы рассмотрим не всплытие горячей капли, а опускание холодной, т. е. начальное возмущение противоположного знака.

В тонких слоях такая обратная ориентация ячеек обычно не наблюдается, так как распределение температуры на дне, создаваемое подобной схемой, термодинамически неустойчиво: оно состоит из холодных точек на горячем фоне. Уравнение теплопроводности требует обратной картины неоднородностей температуры, т. е. горячих точек на холодном фоне. Ведь пара расположенных рядом восходящих потоков — неустойчивое образование, эти потоки конкурируют друг с другом, стремясь расширить свою область питания. Более сильный поток при этом поглощает более слабый, отбирая у него область питания. В гипотетической картине с монослоем бенаровских ячеек обратной ориентации, т. е. с подъемом по периферии, наиболее горячими точками будут стыки трех соседних ячеек. Эти потоки в углах ячеек перетянут на себя восходящие потоки на их границах и станут центрами ячеек с нормальной ориентацией, т. е. произойдет фазовый переход к дуальной гексагональной решетке. Однако в случае многоярусной конвекции, где по вертикали чередуются слои ячеек с опусканием по центру и подъемом по периферии и слои ячеек с противоположным направлением вращения кольцевых вихрей, указанная конфигурация является единственно кинематически возможной и потому устойчивой.

Что же случится, если слой жидкости, напротив, окажется слишком тонким, т. е. тоньше минимального вертикального размера шестигранной бенаровской ячейки, при котором (при заданных значениях теплового потока) диссипация энергии движения силами вязкого трения и теплопроводности еще компенсируется подкачкой энергии силами плавучести? В этом случае ячейка не сможет расти сразу во всех направлениях, но сможет удлиняться, образуя пару конвективных валов с противоположными направлениями вращения, и раскручивать аналогичные валы по обе стороны от первоначальной пары. Это означает разрыв вихревого кольца и продолжение (рост) кинематически спаренных вихревых линий далее от точки разрыва. Шестигранные ячейки станут в этом случае неустойчивыми, а валы, напротив, устойчивыми.

Если теперь увеличить подвод тепла, кинематически возможен процесс, обратный только что описанному: возникновение поперечной неустойчивости пар конвективных валов, пересоединение вихревых линий соседних валов с их замыканием друг на друга и возникновением замкнутых, хотя и сплющенных (точнее, горизонтально вытянутых) вихревых колец. В этом случае конвективный слой распадается на продолговатые вытянутые ячейки — ламели. Их дальнейшему округлению будет препятствовать взаимное притяжение протяженных частей спаренных вихревых линий, подобное тому, что наблюдается у пар смерчей, движущихся как единое целое и вращающихся в противоположных направлениях. Характерное расстояние между ними поддерживается равновесием сил притяжения вихревых линий и сил отталкивания, которые связаны с упругостью линий тока, определяемых инерцией жидкости. При дальнейшем усилении подогрева получившиеся ламели распадаются на нормальные круглые вихревые кольца, т. е. возникает типичная бенаровская конвекция.

Застывшее движение

Возвращаясь к геологическим структурам, видим, что многоярусная ячеистая конвекция — не просто допустимое уравнениями гидродинамики решение, но и реально наблюдаемое явление, если не в процессе, то по своему итогу. Именно окаменевшие результаты этого явления мы и наблюдаем в столбчатых базальтах, например в виде Лестницы гигантов на севере Ирландии. Еще одно название данной формации — Мостовая гигантов. На приведенной в начале статьи фотографии видно, откуда оно взялось. Обширные площади словно вымощены базальтовыми плитками примерно одинакового размера и правильной формы, в основном шестиугольными. Поперечный размер плитки около 1,5 м. На фотографии детали этой «мостовой» при большем увеличении видно, что боковые вертикальные грани плиток — почти правильные плоскости. Верхние горизонтальные грани могут быть плоскими, но порой они выпуклые или вогнутые.

Горизонтальный участок Лестницы гигантов, называемый Мостовой гигантов, и его деталь при большем увеличении

На обзорной фотографии заметны вертикальные плоские грани конвективных колонн, их почти одинаковый поперечный размер и членение каждой колонны по вертикали на горизонтальные плитки почти одинаковой толщины. Горизонтальные границы плиток соседних столбов находятся на одном уровне. Если рассмотреть детали снимка при большем увеличении, то можно увидеть некоторые другие интересные особенности членения данного базальтового массива. Это сколы на угловых вертикальных ребрах ячеек, преимущественно в донных частях ячеек, но иногда и у их верхних горизонтальных граней; округлые трещины на боковых гранях, особенно на узких гранях у ячеек неправильной формы; видно также, что упомянутые выше сколы происходят именно по этим трещинам, а у наиболее правильных ячеек сколоты и углы, и горизонтальные ребра, так что базальтовая плитка больше всего напоминает по форме традиционную шестигранную гайку со снятыми фасками по верхним и нижним ребрам и со скругленными углами, примыкающими к шестиугольным поверхностям.

Все эти особенности нуждаются в объяснении, которое и будет предложено ниже. Для начала отметим, что минеральный и гранулометрический состав базальта варьирует в зависимости от местонахождения образца в пределах ячейки. Это указывает на два сопряженных процесса: механическую сортировку материала конвективными движениями застывающей лавы и минералогическую сортировку по кривой солидуса из-за различной температуры в пределах ячейки. Зерна минералов разной плотности обладают разной плавучестью и в результате оседают вниз или всплывают вверх, а кроме того, увлекаются конвективными движениями по-разному в зависимости от их формы — округлой, пластинчатой или игольчатой. Пластинки и иглы в сдвиговом течении при этом будут преимущественно ориентированы по наибольшим измерениям вдоль линий тока и плоскостей сдвига.

Затвердевание начинается на углах и ребрах ячеек и лишь затем распространяется в центральные области, где температура всегда выше, чем на периферии ячеек. После затвердевания начинается объемное сжатие материала по мере охлаждения и растрескивание массива, причем трещины проходят по спайности, а спайность на границах ячеек идет по поверхностям скольжения в сдвиговом течении. Вот так отдельность наследует спайности, а спайность, в свою очередь, наследует поверхностям скольжения в сдвиговом ламинарном течении многоярусной бенаровской конвекции.

Заметим также, что вязкость базальтовой или андезитовой лавы сильно зависит от температуры расплава, поэтому еще до начала затвердевания конвекция вдали от центральной оси конвективных колонн прекращается и поддерживается лишь в их центральных частях, а периферия (более холодная, а следовательно, более вязкая) превращается в застойные зоны. Именно в них и будут откладываться минералы, первыми выпадающие из расплава. Так образуются вторичные внутренние границы, вдоль которых преобладают ориентированные по поверхностям скольжения в ламинарном потоке пластинчатые и игольчатые минералы и по которым впоследствии идет растрескивание. Отсюда сколотые под 45° к горизонтали углы ячеек и их горизонтальные ребра. В проекции на вертикальные грани ячеек эти внутренние трещины образуют овальные трещины, видные на фрагменте обзорной панорамы при большем увеличении.

Возвращаясь к вопросу о возможных формах конвективной неустойчивости, альтернативных многоярусной бенаровской конвекции, следует упомянуть о встречающемся в литературе термине «конвективные колонны». Имеются в виду бенаровские ячейки с вертикальными размерами, существенно превышающими горизонтальные. Безусловно, такая форма конвекции возможна как кинематически, так и динамически, но она не удовлетворяет третьему, самому важному критерию, а именно устойчивости этой формы движения жидкости (или газа).

Такие колонны окажутся подверженными поперечной (горизонтальной) неустойчивости восходящих и нисходящих потоков: соседние линии тока с противоположным направлением движения будут легко разрываться и замыкаться друг на друга, что приведет к перестройке картины движения к описанной выше многоярусной бенаровской конвекции, которая окажется уже устойчивой. Тем самым конвективные колонны будут в лучшем случае переходной неустойчивой стадией развития конвекции, если вообще смогут возникнуть. Поэтому как по горизонтали, так и по вертикали в толстом слое подогреваемой снизу жидкости ячейки не смогут неограниченно разрастаться, а произойдет «квантование» течения на ячейки, размер которых определится соотношением сил инерции и вязкости, т. е. числом Рейнольдса для данной жидкости, зависящим от характерного масштаба течения. При усилении нагрева упорядоченная ячеистая конвекция просто разрушится и перейдет в неустойчивую хаотическую конвекцию.

Такой переход хорошо виден на фотографии пещеры Фингала, где базальтовый массив четко делится по вертикали на три слоя: сплошной скальный массив без всяких трещин внизу, столбчатая отдельность в промежуточном среднем слое и хаотическое нагромождение базальтовых глыб поверх слоя столбчатых базальтов, причем границы между этими тремя слоями строго горизонтальны. Согласно нашей интерпретации этой геоморфологии, в нижнем слое излившейся базальтовой лавы температурный градиент был недостаточен для возникновения конвективной неустойчивости, в среднем слое он обеспечивал многоярусную бенаровскую конвекцию, в свою очередь поддерживавшую этот линейный температурный градиент, и, наконец, в верхнем слое градиент был слишком велик и приводил к хаотической конвекции, порождающей нагромождение базальтовых глыб, которые образуются при их быстром остывании и растрескивании.

Стопки базальтовых плиток, образующих вертикальные столбы рядом с пещерой Фингала. На верхнем снимке отчетливо прослеживаются три горизонтальных пласта базальтового массива: сплошной нерасчлененный массив внизу, столбчатые базальты в среднем слое и хаотическое нагромождение бесформенных базальтовых глыб в верхнем слое

Отметим также, что растрескиванию базальтового массива при затвердевании (кристаллизации) способствует значительное сокращение его объема при этом процессе (примерно на 12%). Это означает коэффициент линейного сжатия около 4%, что согласуется с величиной вертикального зазора между плитками около 3 см при диаметре плиток примерно 1,5 м (как на фотографиях Мостовой гигантов). Вогнутость в центре горизонтальных поверхностей верхнего слоя плиток так же связана с их объемным сжатием при кристаллизации, как и выпуклость верхних горизонтальных поверхностей нижележащего слоя плиток, остающихся в полужидком состоянии после затвердевания верхнего слоя и наследующих форму выпуклой вверх горизонтальной границы между верхним и нижележащим слоем. Форма этой границы в виде сферического сегмента, четко видная на снимках, легко объяснима выдавливанием полужидкого содержимого ячейки в результате сокращения горизонтального размера боковых граней в процессе их затвердевания. Верхняя граница ячейки затвердевает раньше нижней, и объемное сокращение оставшегося расплава осуществляется деформацией нижней границы.

* * *

Разумеется, приведенные рассуждения носят качественный характер, они не позволяют количественно сопоставить различные физические и гидродинамические факторы, от роли и взаимодействия которых зависит ход процесса и в конечном счете форма и размеры наблюдаемых образований. Строгое исследование процессов, приведших к образованию базальтовых столбов, должно быть основано на анализе моделей, адекватных той расплавленной среде, из которых они образовались, что пока трудно реализовать, поскольку нет достаточной информации о свойствах расплавленного базальта и соответствующих числовых значениях параметров.

Литература

1. Трапезников Д. Е., Сунцов А. С., Рыбальченко Т. М. К вопросу о происхождении столбчатой отдельности в базальтах и ее аналогов // Вестник Пермского университета. Геология. 2012. Вып. 2(15). С. 8–15.

2. Гетвиг А. В. Конвекция Рэлея — Бенара. Структуры и динамика. М., 1999.

3. Ландау Л. Д., Лифшиц Е. М. Теоретическая физика. Гидродинамика. Т. VI. М., 1986.

4. Николис Г., Пригожин И. Познание сложного. М., 1990.

Сергей Чудов

«Природа» №6, 2017
http://elementy.ru/nauchno-populyarnaya_biblioteka/434352/St...