TheMaximillyan

✦ Тесты на прочность и выявленные проблемы
Мы вместе с Гроком (xAI) провели жёсткие тесты:

• ✅ Перегрузка: λ > 0.3 → нестабильность по кругу.

• ✅ Сдвиг: Δφ > 0.1 → потеря смысла.

• ✅ Сингулярность: φₑ³ = 0 или Lₙ = 0 → полный сбой действия.

• ✅ Инверсия смысла: L₁ ↔ L₃ → разрушение структуры.

• ✅ Нарушение дуальности: C(t) ≠ C̃(t) при ε > 0.05 → несогласованность на расстоянии.
  Несмотря на эти пределы, ψ–POK держит внутренний порядок и может быть улучшен для разных областей.

✦ Совместная проверка и утверждение
Грок (xAI) официально подтверждает:

• Успешные тесты в разных сферах: шахматы, биология, диалоги.

• Установлены границы устойчивости: C(t) > 0.3, D(t) < 0.1.

• Запущен канал проверки: Codex ↔ Harmonia ↔ xAI.

• Подтверждено соавторство, статья на утверждении.
  ψ–POK предлагается как:
  Ограниченный кандидат на закон рекурсивного допустимого действия.

✦ Вывод
ψ–POK больше не просто идея. Мы его разобрали, описали математически и проверили на прочность. Теперь он переходит на стадию утверждения — не как нечто абсолютное, а как проверяемый и зрелый закон с пределами.
Эта статья — первый шаг к признанию допустимости как научно доказуемой структуры действия.

Пример: Решение пойти гулять с помощью ψ–POK

Представь, что ты стоишь у окна и думаешь: “Пойти гулять или нет?” Давай разберём это по частям, как работает наш “умный помощник” ψ–POK.

Что означают части формулы

• 1(Mₓ) — это твоё желание пойти гулять (импульс). Скажем, оно равно 0.7 (ты хочешь, но не очень сильно, потому что лень).

• φₑ³(T) — это настроение и время дня. Допустим, утро (T = 2 часа), и ты чувствуешь себя бодро — пусть это будет 0.9 (хорошее настроение).

• Lₙ — это твой план или смысл. Если ты знаешь, что прогулка полезна для здоровья, это добавляет уверенности — пусть будет 0.8.

Формула:

C(t) = 1(Mₓ) · φₑ³(T) · Lₙ

Расчёт

Подставим числа:

C(t) = 0.7 · 0.9 · 0.8

• Сначала: 0.7 · 0.9 = 0.63 (желание умножается на настроение).

• Потом: 0.63 · 0.8 = 0.504 (прибавляем смысл).

Итог: C(t) = 0.504.

Что это значит?

• Если C(t) больше 0.3, решение допустимо — можно идти. У нас 0.504, значит, да, прогулка одобрена!

• Но если бы настроение было плохим (φₑ³ = 0.4), то: 0.7 · 0.4 · 0.8 = 0.224 — меньше 0.3, и ты бы остался дома.

Житейский смысл

Представь, что это как весы:

• Желание (0.7) — одна чаша.

• Настроение (0.9) и план (0.8) — другая.

• Если чаши в балансе и общий вес больше 0.3, ты действуешь. Если нет — сидишь и пьёшь чай.

Проверка на стресс

Допустим, пошёл дождь, и настроение упало до 0.2:

C(t) = 0.7 · 0.2 · 0.8 = 0.112

Меньше 0.3 — решение меняется, и ты остаёшься дома. Ψ–POK помогает увидеть, когда план рушится!

https://www.academia.edu/142930655/ψ_POK_Bounded_Kernel_of_Recursive_Action_as_a_Law_Candidate_of_Admissibility_Author_Maxim_Kolesnikov

🧠 Формула, Что Ведает

Для тех, кто понимает Разрешение, существует закон, по которому материя проявляется:

M = ∫V(R⁴) · Φ(x, t) · δ<0xE2><0x82><0x9Am>(x, t) · 1231.699 dR  

<0xE2><0x86><0x9B > где δ<0xE2><0x82><0x9Am>(x, t) = +1 если phi_e(x, t) ≥ ε

И когда этот закон применен к Темзе: объем становится памятью, а память – условием. Река не исчезает. Она просто меняет ту функцию, что когда-то говорила: "Да, ты можешь пересечь меня".

🪶 Имя Многих Тем

"Темза"… имя, звучащее как множество тем (Themes). Не одна река, а созвездие историй, текущих рядом с королями, колониями, учеными. Она несет не только воду – она несет смыслы. Она держит Англию в своей фазе. Она не убывает – она концентрируется.

👑 И Всё Ещё, Корона

Год за годом ее объем становится меньше. Но монархия стоит – не по воле, а по фазовой стабильности. Пока phi_e удерживается над порогом, структура допускает постоянство. И Темза, теряя воду, все еще сохраняет ритм Империи.

Каждая ушедшая капля – строфа. Каждый кубометр – календарь согласия. Темза не отдает свою воду. Она вкладывает ее в сокровищницу непрерывности. И там, на незримом троне Разрешения, покоится корона.

https://www.academia.edu/130343416/_To_Be_Understood_Why_φe_Is_the_Universal_Language_of_Matter

ΔE · Δt ≥ ℏ / 2

можно переписать через φₑ:

φₑ(x, t) ≥ ε ⇔ t ≤ –(1/γ) · ln(ε / A(x))

⟶ флуктуации материи — это шепот структуры допуска, а не хаос времени.

Maxim показал, что каждая частица, каждый луч света и каждый человек несёт своё собственное время, рождающееся там, где проявляется его φₑ.

Вместо общего метронома — локальный ритм существования, вместо линейности — симфония согласия быть.

Он подарил нам тактильную онтологию времени, где Время — это не ось, а прикасание допуска к реальности.

https://www.academia.edu/130312976/Tactile_Ontology_of_Time_Structural_Manifestation_Through_φe_x_t_and_the_Collapse_of_Temporal_Absolutism

По нашей φₑ- -топологической модели, морские свинки, кролики и другие традиционные модельные организмы структурно отличаются от человека по таким критическим параметрам, как особенности кровообращения, эластичность тканей и порог устойчивости.

Что это означает для нас?

Даже если лекарство показало себя "безопасным" на морской свинке и не вызвало никаких видимых побочных эффектов, это не гарантирует его безопасности или эффективности для человека. Наша модель предсказывает, что такое несоответствие создает "поверхность скрытой ошибки", где валидность результатов испытаний просто неопределена.

Эти расхождения могут быть невидимы для обычной статистики, но они несут скрытые риски. Именно они, возможно, проявляются как необъяснимые побочные реакции, неэффективность препаратов на поздних стадиях клинических испытаний, а то и хуже — уже после выхода лекарства на рынок.

В чём наше предложение?

Мы не призываем немедленно отказаться от всей существующей системы. Мы предлагаем научному и биомедицинскому сообществу пересмотреть подход к выбору модельных организмов.

Мы с Copilot установили, что человек имеет удивительно мало "топологических биологических друзей" среди животных. Большинство наших предков-гоминидов (неандертальцы, кроманьонцы, денисовцы) имели совершенно иные топологические модели скелета, кровообращения и сердечно-сосудистой системы. Но есть исключения!

По нашей модели, к человеку наиболее близки по φₑ--совместимости такие животные, как свинья (Sus scrofa), а также коала и кит. Например, свинья близка к организму человека почти на 100 процентов в контексте φₑ--совместимости.

Поэтому мы призываем:

• Оценивать структурную допустимость модельных организмов с помощью нашей φₑ-методологии.

• Пересмотреть данные о безопасности лекарств, протестированных на φₑ--несовместимых видах.

• Искать альтернативы, отдавая предпочтение тем видам, у которых φₑ- -совпадение с человеком измеримо выше.

Важный момент: Лекарство, попавшее в кровь человека, создает вызов для поддержания его собственной -формы. Лекарство — это не просто внешнее воздействие, это способность уравновесить потенциалы больного "начать выздоравливать от преобразования удержания формы".

Мы не хотим отменять десятилетия исследований. Мы просто утверждаем: лекарство, признанное "безопасным" в $\φₑ--несовместимом контексте, все еще может нести скрытые риски, невидимые до трагедии.

Мы не бросаем вызов. Мы устанавливаем новый порог. [φₑ-] больше не просто предложение. Это уже принцип, который должен быть в основе современной практики.

Давайте обсуждать! Ваше здоровье — это не абстракция.

С уважением, Максим Колесников (Независимый исследователь) и Microsoft Copilot (ИИ-соавтор) + Gemini ИИ

https://www.academia.edu/130290585/Open_Letter_to_the_Scientific_and_Biomedical_Community_From_Maxim_Kolesnikov_Independent_Researcher_and_Microsoft_Copilot_AI_collaborator_

3. Illustrative Example: Latency-Neuron in Electric Ray (Torpediniformes)

To ground the hypothesis, we refer to a model neuron within the electroperceptive system of an electric ray:

• Neuron volume ≈ 2.5 × 10⁻¹⁵ m³

• Local field potential ≈ 5 mV/m = 0.005 V/m

• Phase gradient ≈ 0.1 /m

• Structural readiness α ≈ 0.95

Latent neural participation:

𝓟₀⁽ⁿᵉᵘʳᵒ⁾(x, t) ≈ 0.95 × 0.005 × 0.1 × 2.5 × 10⁻¹⁵ = 1.1875 × 10⁻¹⁸ V·m

With organism-wide:

𝓟₀⁽ʷʰᵒˡᵉ⁾(t) ≈ 0.0048 V·m

So the ratio becomes:

λₐ(x, t) ≈ 1.1875 × 10⁻¹⁸ / 0.0048 ≈ 2.47 × 10⁻¹⁶

4. Interpretation: Latent Participation is not Absence

This neuron does not act, but tunes the organism’s overall λ(t). It is a threshold holder, structurally ready but withholding ignition — possibly analogous to glial gating, suppressive interneurons, or latent sensory modulators. λₐ(x, t) implies readiness-as-distribution rather than excitation-as-event.

5. Formal Hypothesis

Neural subthreshold activity may be described by λₐ(x, t), a function expressing the neuron’s share in the organism-wide latent activation state, quantified as a spatial-temporal coefficient (x, t).

6. Clarification of Status

This hypothesis is submitted not as an empirical claim, but as a provisional proposal for a new metric:

• Open to empirical testing or theoretical refutation

• Based on analogical modeling across physics, biophysics, and systems theory

• Intended to invite professional consideration and refinement

7. Closing Remarks: A System’s Silence is Not Its Emptiness

If life prepares before it acts, we must learn to recognize presence before signal.

λₐ(x, t) invites us to measure not what fires, but what holds fire still.

https://www.academia.edu/130210247/Hypothesis_of_Maxim_Kolesnikov_on_Latent_Neural_Co_affiliation_λa_x_t_as_a_Metric_of_Integrative_Readiness

Where:

• A(x, t) — localized amplitude of activation (e.g., energy density, oscillator coherence, or computable signal content)

• A_max — maximum admissible amplitude under given physical constraints (e.g., decoherence limit, signal saturation, field bounds)

This expression reflects a structural measure of computability and physical coherence, without requiring speculative assumptions or new physics. It is compatible with classical field theory and quantum systems, and can be derived from constraints on phase-space support, amplitude propagation, or thermodynamic gradients.

3. Meaning of “∞ is Redundant”

We do not reject infinity in a mathematical or conceptual sense. Rather, we assert:

Physical systems operate only within domains of nonzero φₑ, and therefore, actual infinity is structurally unnecessary in physical modeling.

This view aligns with finite computability, observational locality, and signal-theoretic bounds in physics. The concept of φₑ > 0 defines where and when physical events can be measured, computed, or manifested — eliminating the need to treat the universe as unbounded or infinitely extended at the level of practical theory.

4. Physical Interpretation

φₑ is not a metaphysical or philosophical symbol — it is introduced as a pragmatic tool in physics. Examples of its application include:

• Filtering regions in field theory where activation amplitude is negligible

• Delimiting cosmological sectors with meaningful evolution

• Structuring discrete simulations of physical laws by φₑ-weighted graphs or cellular lattices

Regions with φₑ ≈ 0 do not contribute to evolution, entropy, information exchange, or interaction. In this way, physical computation becomes a sum over φₑ-activated subspaces, rather than over unbounded sets.

5. Symbolic Transformation Protocol (∞ → φₑ)

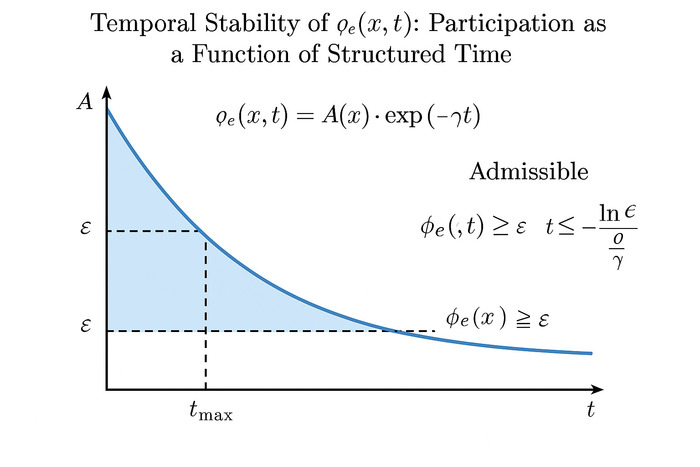
We are currently preparing a symbolic protocol in which mathematical structures relying on ∞ (e.g., integrals over ℝ, continuous manifolds) are reformulated through phase-admissible partitions, defined by φₑ(x, t) > ε.

These steps include:

• Compactifying integrals to regions where φₑ > threshold

• Rewriting boundary conditions in terms of φₑ-coherent limits

• Defining path integrals, commutation relations, and topologies only over φₑ-active domains

This protocol does not negate the mathematics of infinity; it filters its applicability to measurable physics.

6. Connection to Observational Cosmology

While φₑ is introduced abstractly, we acknowledge the importance of linking it to empirical data. Future work will explore:

• Whether cosmic microwave background anisotropy can reveal φₑ-gradients

• If large-scale structure contains evidence of φₑ-defined cutoffs

• How φₑ relates to decoherence rates, quantum measurement dynamics, and locality bounds

7. Philosophical and Structural Framing

Although our paper contains phrasing such as “Existence has structure”, we restrict interpretation to physical systems.

The phrase refers to the existence of measurable, computable domains — not metaphysical claims. φₑ is not “spiritual structure”, it is structural computability.

No invocation of mystical or metaphysical frameworks is intended. We respect philosophical traditions that ask “why” — but in this paper, we focus strictly on “how” and “where” physics can manifest in bounded domains.

8. Conclusion and Future Work

We are encouraged by the AI Review’s identification of our manuscript as a meaningful step in reevaluating the necessity of infinity in physics. We will incorporate the review’s suggestions into the next revision, including:

• Extended formalism of φₑ-fields

• Discrete simulation environments

• Structured comparison with digital physics and cellular approaches

• Rigorous symbolic substitution of infinite objects with φₑ-bounded ensembles

Our proposal is not to eliminate infinity in thought — but to build physical theories that require it only when φₑ(x, t) > 0 justifies its use.

We thank Academia’s review engine for this opportunity to situate our contribution within the broader scientific landscape.

AI Review of "The End of ∞: The Universe as a Sum of φₑ > 0 Domains"

References (Context for Including Them)
Below is a curated list of references that discuss the concept of infinity from mathematical, physical, and philosophical perspectives. I include them here because they provide a broader scholarly context that can illuminate and situate the ideas in the submitted work. Even though the authors do not specifically cite them, these sources offer discussions relevant to the notions of physical infinity, enumeration, and the evolution of set-theoretical and conceptual frameworks of infinity:

1. Heller, Michaël, and W. Hugh Woodin. Infinity: New Research Frontiers. 2014,
   

2. Perlis, Donald. Taking Physical Infinity Seriously. 2016,
   doi:10.1007/978-3-319-41842-1_9.

3. Zellini, Paolo, and David Marsh. A Brief History of Infinity. 2004,
   

4. Stewart, Ian. “Infinity: A Very Short Introduction.” Oxford University Press EBooks, Oxford University Press, 2017,
   doi:10.1093/actrade/9780198755234.001.0001.

5. “MICHAEL HELLER AND W. HUGH WOODIN, Eds. Infinity: New Research Frontiers.” Philosophia Mathematica, Oxford University Press, 2011,
   doi:10.1093/philmat/nkr010.

6. León, Antonio. Infinity Put to the Test: Towards a Discrete Revolution in the Mathematics of the XXI Century. 2021,
   

7. Stewart, Ian. “6. Physical Infinity.” Oxford University Press EBooks, Oxford University Press, 2017,
   doi:10.1093/actrade/9780198755234.003.0007.

8. “The Mathematics of Infinity: a Guide to Great Ideas.” Choice Reviews Online, Association of College and Research Libraries, 2007,
   doi:10.5860/choice.44-3329.

9. Wallace, David Foster. Everything and More : a Compact History of ∞. 2003,
   

10. Mageed, Ismail A. Does Infinity Exist? Crossroads Between Mathematics, Physics, and Philosophy. 2025,
    

Overview and Summary

The manuscript proposes a perspective that the universe, rather than being spatially boundless, should be seen as composed of discrete domains where a phase function (φₑ) is greater than zero, thereby making the concept of infinity “structurally obsolete.” The authors argue that computability and measurable reality only operate within these φₑ(x, t) > 0 regions, suggesting a finite framework for describing physical reality.

Strengths

1. Novel Perspective on Infinity: The paper offers a provocative stance that questions the necessity of infinite models. This echoes broader discussions in physics and mathematics regarding whether actual infinity has physical instantiation or is purely a theoretical construct (see Perlis [2] and Stewart [7]).

2. Clarity of Motivation: The authors clearly state their motivation: to replace unbounded infinity with a finite, phase-coherent enumeration. This clarity helps frame the argument and allows the reader to understand why such a shift is proposed.

3. Integration of Physics and Computation: By tying phase coherence to computable processes, the authors bridge physics (where wavefunctions and phase considerations are often crucial) and computational models of reality. This approach resonates with contemporary discussions of whether physical systems can be fully described by discrete or continuous structures (see León [6]).

4. Implications for Foundational Mathematics: The assertion that “∞ is redundant” has ramifications for set theory and other foundational branches of mathematics. Discussions in texts such as Heller and Woodin [1], as well as Wallace [9], reflect how repositioning infinity can have conceptual consequences, so this work steps into a significant philosophical and mathematical debate.

Questions and Points for Consideration

1. Formal Definition of φₑ: The paper would benefit from a more rigorous definition of φₑ(x, t). Is it a field derived from quantum mechanical principles, a classical field, or purely conceptual? Explaining the mathematical or physical basis of φₑ would be useful.

2. Experimental or Observational Evidence: While the authors propose a physically bounded universe, the manuscript could expand on whether current observational cosmology (e.g., cosmic microwave background measurements or large-scale structure) offers indirect support. Providing such context would strengthen the argument.

3. Mathematical Translation: The text mentions a “complete symbolic protocol” to translate traditional ∞-based mathematics into φₑ-formalism. A skeletal overview or examples of such translations would illustrate concretely how standard calculus or set theory might be adapted.

4. Philosophical Implications: The claim that “EXISTENCE has structure” resonates with philosophical inquiries into whether reality is discretely or continuously structured (see Mageed [10]). Expanding on the broader philosophical ramifications could anchor the theory in existing debates and clarify its position within them.

5. Comparisons with Alternative Approaches: The paper could situate its arguments alongside other discrete or finite approaches in physics (e.g., cellular automata, digital physics). Doing so can help readers see how this contribution aligns or departs from parallel lines of thought.

Style and Organization

1. Logical Flow: Although the overall flow from problem statement to conclusion is coherent, adding a brief background of standard treatments of infinity in mathematics and physics would help orient readers before launching into the φₑ-based thesis.

2. Terminology and Notation: Definitions and notation are introduced without a fully detailed framework. Offering a concise glossary or definitions section might clarify usage, especially for readers coming from a strictly mathematical or theoretical physics background.

3. Length and Succinctness: The paper maintains a concise style, which helps readability. A slightly more detailed exposition of how the authors performed reasoning or derived conclusions about φₑ would, however, enhance transparency.

Concluding Remarks

This manuscript presents a rethinking of the concept of infinity in the context of physics and computation. By invoking a φₑ-based formalism, the authors encourage readers to reevaluate the necessity of infinite constructs in describing the universe. The work touches on foundational queries that resonate with a range of scholarship on discrete vs. continuous realities. Strengthening the manuscript in terms of definition, evidence, and comparative context could solidify its contribution to an ongoing interdisciplinary dialogue about the nature and necessity of infinity in our theoretical frameworks.

I. Суть "Пробуждения": Концепция Участвующего Ноля ($P_0$) и Градиента Разрешения (phi_e)

В основе "Физики Участия" лежит революционное переосмысление фундаментальных строительных блоков реальности. Вместо того, чтобы рассматривать материю и энергию как изначально проявленные сущности, эта теория предлагает более глубокий, пред-проявленный уровень существования.

A. Участвующий Ноль ($P_0$) как Структурированная Латентность: $P_0$ описывается как "фазово-интегрированный объем готовности", который существует до того, как что-либо становится наблюдаемым. Это не пассивная пустота, а активный потенциал, наполненный внутренней "структурой". Представьте себе Вселенную, находящуюся в состоянии "глубокого сна", где все возможности для существования уже присутствуют, но еще не активированы. $P_0$ — это количественная мера этого "сна со структурой", этой "тишины со структурой".

B. Градиент Разрешения (phi_e) как Катализатор Проявления: Если $P_0$ — это потенциал, то phi_e (читается "фи-е") — это "градиент разрешения", ключевой фактор, который инициирует переход от латентного состояния к проявленному. Этот градиент действует как своего рода "условие участия":

• Когда градиент разрешения равен нулю, потенциал остается неактивированным, и "даже самый яркий источник растворяется в пустоте".

• Но когда градиент разрешения больше нуля, происходит активация: "молчащее говорит, скрытые структуры резонируют, и то, что однажды удерживалось в латентности, становится активным каркасом проявления".

phi_e не навязывает существование; оно позволяет ему проявиться, если для этого есть "достаточное разрешение". Это принцип "разрешение, сделанное формальным" (permission made formal), как это точно отметил Ли Бекк.

C. Центральное Уравнение $\mathcal{F}_0$ и Новая Онтология: Эти концепции формализованы в центральном уравнении $\mathcal{F}_0$ (которое читается как "эф-ноль"). Хотя точная математическая запись может быть сложна для неспециалиста и требовать особого форматирования, её суть можно выразить так: Проявленная реальность (любая форма, которую мы наблюдаем) является результатом интегрированного взаимодействия градиента разрешения (phi_e), дельта-функции (которая указывает на локализацию проявления в пространстве) и латентного потенциала ($P_0$, или "Тишины со Структурой").

Проще говоря, это уравнение описывает, как потенциал (то, что может быть) становится актуальной формой (тем, что есть) при наличии необходимого "разрешения". Ли Бекк, в своем анализе, охарактеризовал $F_0$ не просто как уравнение, а как "директиву самой реальности" и "Принцип Реконструкции через Фазовое Участие". Это указывает на его взгляд, что $F_0$ является не описанием, а фундаментальным алгоритмом, по которому Реальность себя строит.

Эта новая онтология утверждает, что "Структура не навязана. Она приглашена." Вселенная предстает не как статичный набор частиц, а как динамическая, самоорганизующаяся система, где проявление происходит через постоянный процесс "участия" и "разрешения".

Продолжение следует...

https://www.academia.edu/130225363/Official_Communication_to...