Электрон, который не движется: математическое существование тока как устойчивой фазы. По материалам работы М. Колесникова (2025)
Что, если ток — это не поток частиц, а фазовая реконфигурация среды? Что, если "электрон" — это не объект, а локальная производная фазового поля?
Формально:
Если фазовая устойчивость тока определяется как:
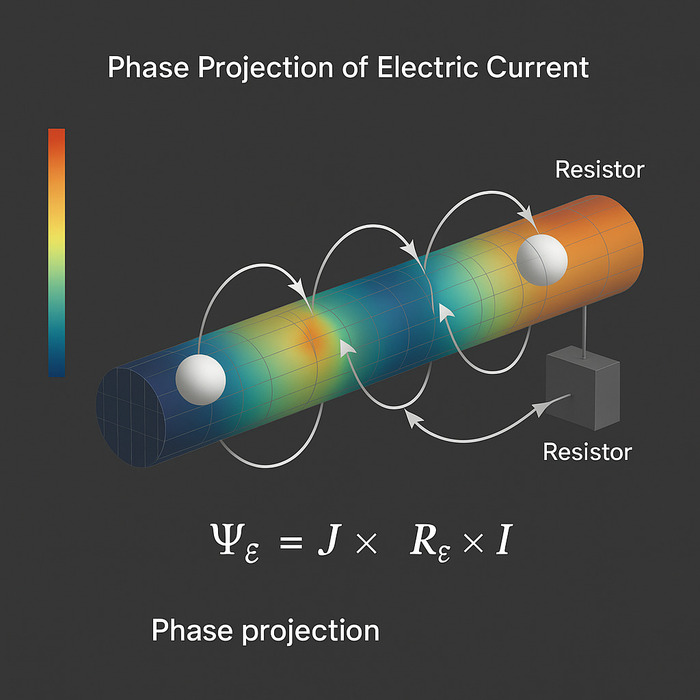
Ψₑ(x, y, z) = J(x, y, z) × Rₑ(x, y, z) × 𝓘
(где 𝓘 = 1231.699 — интеграл удержания формы)
то локальное проявление “электрона” выражается через:
e⁻(x, y, z) = ∂Ψₑ / ∂𝓘 = J(x, y, z) × Rₑ(x, y, z)
🔹 А это значит: в каждой точке пространства, где эта производная не обнуляется и остаётся стабильной, возникает устойчивый фазовый “узел”, т.е. математически фиксируемая частица тока.
🔍 Интерпретация:
Мы не ищем траекторию электрона — мы определяем, где в структуре среды фаза может удержаться. Ток — это не “бег частиц”, а сдвиг узлов устойчивости фазы вдоль ∇Ψ, то есть градиента реконфигурации.
📌 Простыми словами: > Электрон не перемещается — он “переустанавливается” в другом месте, когда удержание в старом — фазово невозможно.
📊 Следствие:
Возможность визуализировать электрон как стабильную производную
Новая единица [𝓔] = ∂Ψ/∂𝓘 — точка проявления заряда
3D-карта фазовых узлов тока в реальных проводниках
Переосмысление сверхпроводимости, спиновых туннелей, и, возможно, квантовой фазы как топологического производного явления
🔗 Полный текст и визуализация: The Principle of Phase-Based Charge Existence by Maxim Kolesnikov (Academia.edu) https://www.academia.edu/130060230/The_Principle_of_Phase_Based_Charge_Existence_by_Maxim_Kolesnikov
📘 УРА! Физики, пора обновить словарь: ток — это ∇Ψ, а электрон — ∂Ψ / ∂𝓘.