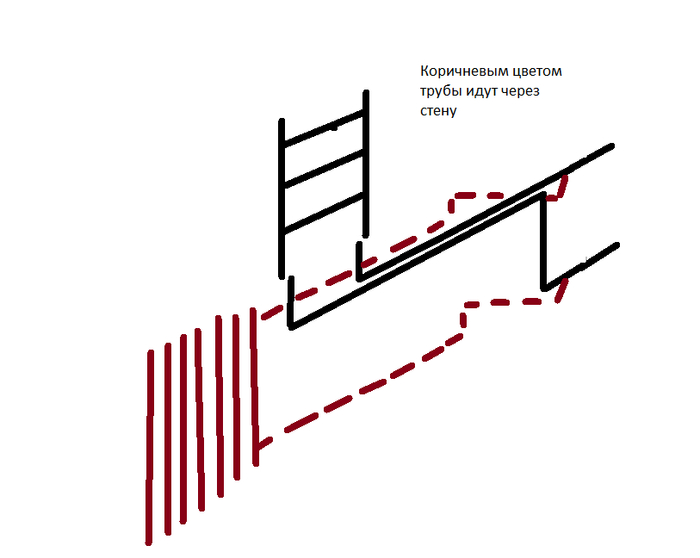
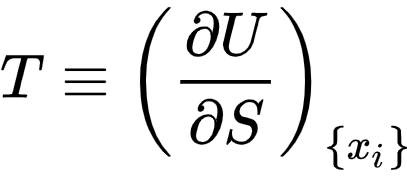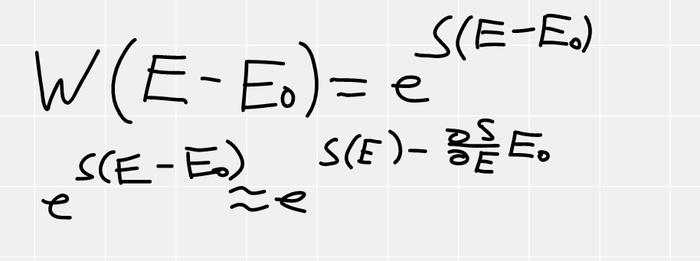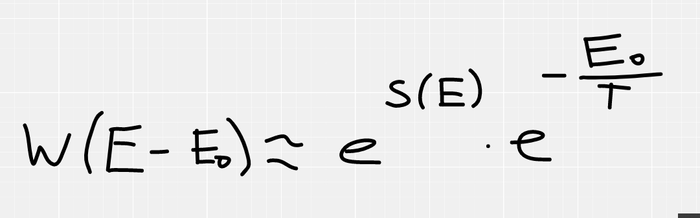В своём прошлом посте я остановился на том, что о температуре как физической величине, люди мало что знают. В школе так вообще отделываются лишь "мерой движения молекул" и на этом заканчивают. А ведь это довольно любопытная штука, смысл которой далеко за простой "средней энергией частиц". Давайте попробуем разобраться, что про неё известно и какие определения температуры есть, и можно ли как-то например дать температуру одной молекуле.
Если копаться всерьез, то очень больно для головы. Потому что количество определений для температуры слишком большое. У разных разделов физики порой разные определения, так и даже в самой термодинамике есть куча вариантов аксиоматики. На одной вики их штук 10, если копать научные статьи, то вполне можно еще десяток другой вариантов найти. Мы не полезем в эти дебри и разберем лишь два определения, первое из классической термодинамики, второе из статистической физики (в которой становится понятнее, как всё же её пощупать можно).
Если грубо разделить аксиомы классической термодинамики на две группы, то в одних аксиоматических построениях температуру просто постулируют как некую физическую величину, которая просто есть (неопределяемая переменная), является интенсивной величиной и количественно выражает интуитивное понятие о различной степени нагретости тел. В других построениях, как неопределяемую базовую переменную вводят энтропию, а температуру определяют как частную производную энергии от энтропии.
Хоть эта запись и пугает всех, кто не знаком с курсом математического анализа, на человеческом языке, она означает "температура это скорость роста энергии при росте энтропии, при неизменном объеме, массе веществ, площади поверхностей и т.д."
Отлично, а что там в статистической физике? Ну условно, там та же формула, что и на картинке выше. Но лучше показать на простейшем примере.
Для примера я возьму систему с десятью монетками. Давайте договоримся, что если монетка орлом вверх, то она имеет энергию 0, если решкой вверх, то энергия такой монетки будет у нас 1.
У системы на картинке энергия 2. У системы с десятью орлами, энергия будет 0. В прошлом посте я объяснял, как считают энтропию в статистике. Так что давайте посчитаем сколько микросостояний дает нам разную энергию.
E = 0 можно получить имея все монетки орлом вверх, это одно состояние, энтропия 0.
E = 1 можно получить имея одну решку, она может быть на первом, втором... и т.д. месте, микросостояний 10, энтропия k*ln10
E = 2 еще больше вариантов, их 45, а энтропия k*ln45
E = 3, вариантов 120, энтропия k*ln120
и т.д.
Реальные физические системы с таким простым набором состояний существуют, например система спинов в магнитном поле: типичная начинка квантового компьютера, атомы водорода в ЯМР спектрометре или они же в томографе.
У обычных больших тел (стакан воды, суп на плите, пробирка) квантовых состояний в невероятное количество раз больше, но с ростом энергии количество возможных вариантов аналогично растет, функцию E(S) можно вполне себе считать непрерывной. Для макрообъектов расстояние между уровнями энергии настолько мало, они так сгущаются, что измерить этот зазор невозможно даже в теории. Энтропию можно ввести и через классическую механику, рассматривая молекулы как шарики, правда там немного иначе она будет считаться, но ответ совпадает с квантовым рассмотрением.
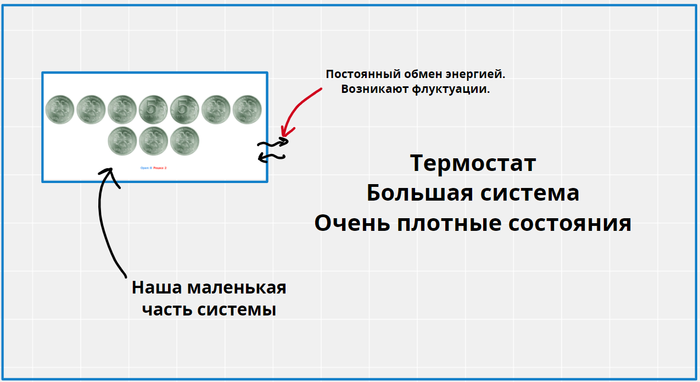
Внимательные наверное уже заметили, что в определении температуры формула содержит производную, а в примере у меня дискретная функция, у которой нельзя посчитать производную. Именно так, понятие температуры в строгом смысле работает только для макроскопических объектов с кучей уровней, где мы не можем заметить, что функция E(S) дискретная. Для описания температуры объектов с малым количеством уровней, приходится сначала утверждать, что такая система находится в состоянии термического равновесия с термостатом (модельная среда, с конкретной температурой), но тогда наша система уже не имеет конкретную энергию, и имеет лишь вероятности находиться на том или ином уровне, ведь между маленькой системой и большим термостатом возникают флуктуации. Эти вероятности легко посчитать, пользуясь нашими формулами. Собственно для маленьких систем, температура уже будет иметь немного другой смысл, и быть скорее параметром, который описывает распределение вероятностей по уровням. О как!
Возьмем всё ту же систему с монетками, и попробуем выяснить как температура окружающей среды будет влиять на её энергию. Представим, что она находится в равновесии и контакте с какой-то другой системой, огромной по сравнению с ней, но при этом конечной.
Всё вместе мы представим изолированной системой с энергией E. Попробуем найти вероятность быть нашей системе в каком-нибудь состоянии с энергией E0.
У нас вся система, обладает каким-то набором микросостояний, пусть их W штук. Нам просто нужно найти сколько из них, подходят нам и поделить это число на общее количество.
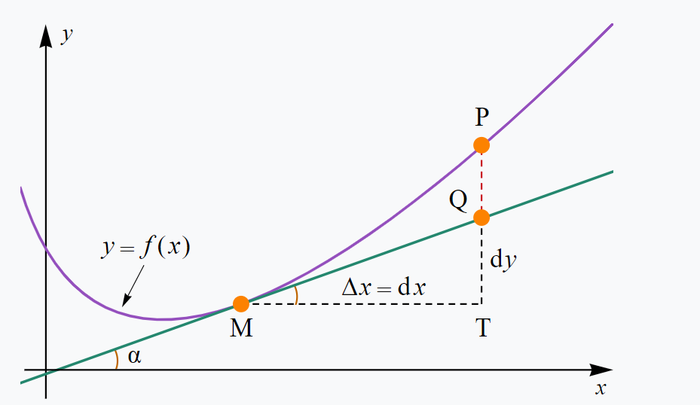
Если наша подсистема, в состоянии с энергией E0, то на термостат остается E-E0. Учитывая, что W=exp(S), получаем, что вероятность пропорциональна exp(S(E-E0)), но как это посчитать? Мы не зря посчитали, что термостат НАМНОГО больше чем наша подсистема, поэтому E0<<<E, а значит мы можем воспользоваться приближенным вычислением (в данном случае оно оказывается точным) с помощью производной. Рядом с точкой M, функция почти не отличается от своей касательной, в этом смысл дифференциала и производной.
Во всем выводе я убрал константу Больцмана, считайте, что я принял её единичкой, это не так важно.
В формуле появилась производная энтропии от энергии (что есть 1/T по определению из начала поста). И в конце концов мы получаем
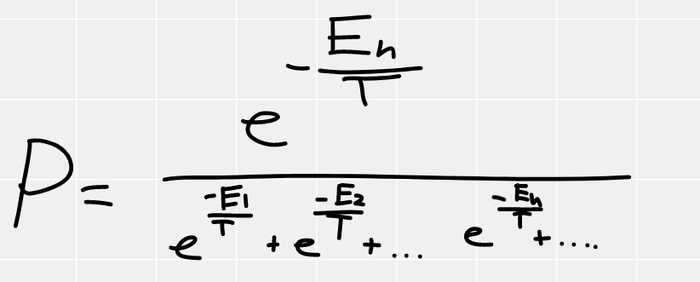
Вероятность должна быть пропорциональна W, при этом в сумме они все должны давать единичку, поэтому вероятность нашей маленькой системке находиться в n-ом состоянии (у которого энергия En), будет
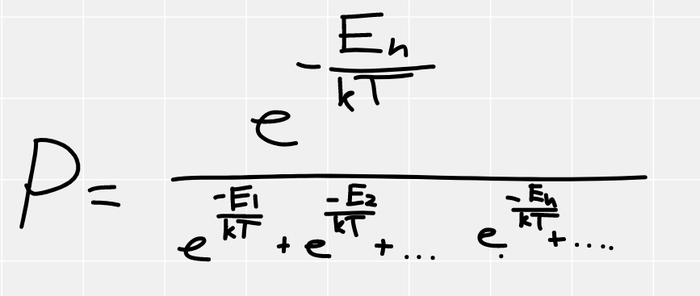
Если вернуть везде постоянную Больцмана, получится так
Снизу в формулах энергии всех остальных уровней. Очень симпатичная формула, называется распределением Гиббса. Из неё можно вывести распределения Максвелла, Больцмана и прочие прекрасные частные случаи. По ней видно, что если температура абсолютный ноль, то система находится в низшем состоянии с вероятностью 1, если же температура бесконечна, то система равновероятно может находиться во всех состояниях от низшего до наивысшего, что немного контринтуитивно (кажется, что бесконечная температура, это наивысшее состояние по энергии), но как видите это не так. Температура это сложный статистический параметр, а не просто энергия тела как нам кажется интуитивно.
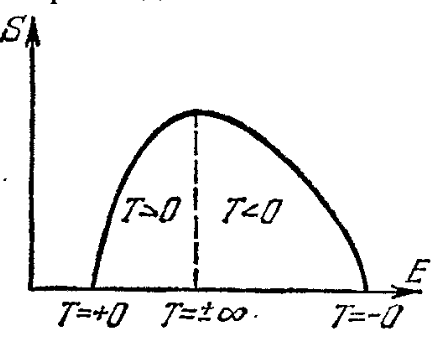
Еще один интересный вывод из такой формулы вытекает если наша система имеет конечное количество состояний (как наш пример с монетками имеет всего 1024 состояний, и 10 уровней), то возможно представить себе отрицательную температуру. Это состояние будет отвечать энергии системы даже большей чем, энергия системы при бесконечной температуре, ибо высшие уровни заселены чаще чем низшие (при бесконечной они поровну все заселены). Мы можем создать искусственно такие состояния в реальности, ведь системы с ограниченным количеством уровней существуют, а способы "перевернуть заселенность" существуют.
Но откуда же у нас всех берется знание, что температура отвечает за скорость молекул? А дело в том, что если мы применим распределение Гиббса к идеальному газу, то средняя кинетическая энергия молекулы будет 3/2kT, об этом нам рассказывают в школе сразу в готовом виде (исторически температуру с этого случая вводили и в науке), и на этом же эту тему заканчивают, отсюда и остается подобный обрубок понимания довольно сложного понятия температуры.
Учитывая, что статистическая физика и термодинамика стоят на очень простых принципах из математики, выходит довольно любопытная ситуация. Дело в том, что и общая теория относительности, и квантовая механика отлично стыкуются с термодинамикой. Но как мы знаем, между собой ОТО и КМ очень плохо стыкуются, и квантовую теорию гравитации до сих пор не разработали. Так же мы знаем, что внутренности и поверхности черных дыр, обладая страшной кривизной пространства-времени, должны описываться той самой пока несуществующей квантовой теорией гравитации, но мы точно понимаем, что эта теория должна тоже хорошо стыковаться с термодинамикой. Изучение термодинамики черных дыр сразу показало, что они должны обладать температурой и излучать, позже Хокинг более подробно описал это излучение, которое назвали в его честь, но это уже совсем другая история.
Закончу пост цитатой Эйнштейна:
«Теория производит тем большее впечатление, чем проще ее предпосылки, чем разнообразнее предметы, которые она связывает, и чем шире область ее применения. Отсюда глубокое впечатление, которое произвела на меня классическая термодинамика. Это единственная теория общего содержания, относительно которой я убежден, что в рамках применимости ее основных понятий она никогда не будет опровергнута»
Эйнштейн А. Собр. науч. трудов М.: Наука, 1967. Т. 4. с. 270