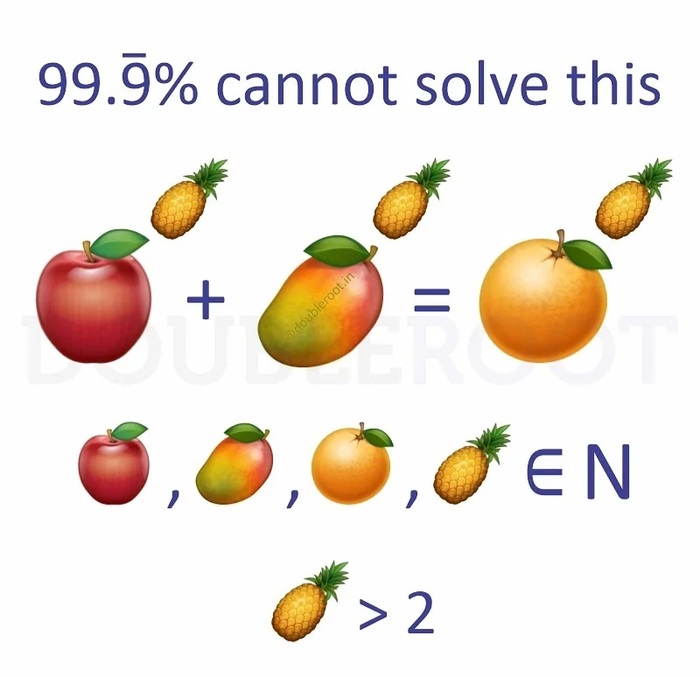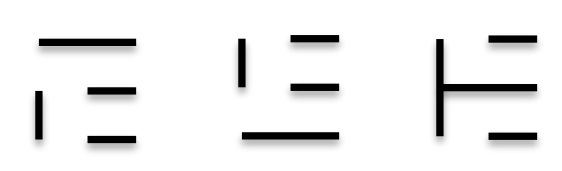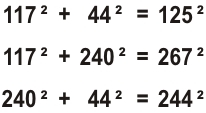Задача из ЕГЭ 2022 на теорию чисел, которую решит шестиклассник
Известно, что a,b,c,d,e и f - это различные, расставленные в некотором, возможно ином, порядке числа 2,3,4,5,6 и 16.
а) Может ли выполнятся равенство a/b + c/d + e/f = 6?
Происхождение арабских чисел - новая теория
Хочу поделится своей теорией о создании символов арабских чисел. Сама теория немного нестандартная и многим покажется слишком сложной, поэтому попробую написать максимально читабельно.
Итак, есть три символа, которые легли в основу изображения арабских чисел, вот они:
Это первая группа. Если перевернуть на 180 гр. эти символы, то получим вторую группу, итого 6 шт.В моей книге они называются "прямые символы" .
Теперь самая интересная часть. Попробуйте последовательно наложить символы из первой колонки на символы из второй. Вот что получается:
Перед вами символы 8 из 10 арабских чисел. Происхождение чисел 4 и 7 немного отличается. Если вам интересно происхождение "прямых символов", а так же история числа 4 и 7 - переходите на мой сайт www.math1-9.com
Задачи
Всем привет, Hello all, Мое имя Олег Олегович, меня интересует вопрос ? числа 40 ! 41 , 42 факториал и 43 . Вопрос ? 40 ! + один может ли ответ поделить на 41. А также число 42! разделить 43, по той же схеме. И сделать это так, чтоб было всем понятно и ясно. И ещё одна задача. Меня интересует вопрос такой, итак, вот можно ли перемножить все числа с 5 до 70, кратные 5 или 8, на листе бумаги. А на этом всё, всем пока.
Теории чисел и математика
Привет обществу Пикабу. И так далеше"
pikabu. Вот я хочу спросить знает ли кто-нибудь какой-нибудь журнал который я могу написать о''своём решении, известной гипотезы из задач, известной, гипотезы, Birch - Swinernton, Diear. и как всегда малая теорема Ферма. А также " хочу сказать вот что, что у меня имеется ответ n : ) 3, быстрый способ нахождения а ^z; равно ли число 3 степени.
Так как число в кубе почти всегда равно математической прогрессии" при складывании 2 таких чисел не квадратные не кубические решения потом не образуется. Поэтому-то если кому-то это интересно, & захочет помочь найти др, редакций, интересных газеты пусть мне напишет ответ комментарии. По какому адресу можно было бы в этом написать. Также прошу глупости там не писать, все пока чао.
Кирпичи Эйлера. 2-я параметрическая формула!
Привет! Меня зовут Игорь, и здесь я поделюсь некоторыми своими знаниями о т.н. кирпичах Эйлера. Более того, Вы станете свидетелем настоящего открытия, которое сами же и сможете проверить.
Часть 1. История
Существуют прямоугольные параллелепипеды (кирпичи) у которых все грани и диагонали являются целыми.
Например, кирпич со сторонами 117, 44, 240 имеет целые диагонали, которые можно вычислить по закону Пифагора, как:
За предыдущее время исследования этой задачи (более двух веков) была найдена только одна «параметрическая» формула, которая всегда дает на выходе эйлеров кирпич.
Эта формула выглядит так:
ПАРАМЕТРИЧЕСКАЯ ФОРМУЛА №1 ДЛЯ КИРПИЧЕЙ ЭЙЛЕРА
x — нечетный
y — четный (пониженный)
и, если их подставить в формулу, то получается эйлеров кирпич:
Эта формула не покрывает все известные кирпичи. Получаемые по формуле значения нужно брать по модулю, поскольку иногда они получаются отрицательными. Это имеет четкий геометрический смысл, о котором я пока умолчу :-)
Примечание 1. На данный момент эйлеровы кирпичи рассчитываются по большей части компьютерным перебором. Вот, например, грамотно составленный список, с т.н. примитивными кирпичами (не имеющими общего множителя):
Несколько примеров. В первых скобках целочисленная пифагорова тройка, во вторых скобках — эйлеров кирпич, полученный по параметрической формуле №1, потом следует номер в «грамотно составленном списке».
(3, 4, 5) = (117, 44, 240) — №1
(5, 12, 13) = (2035, -828, 3120) — № 11
(15, 8, 17) = (-495, 4888, 8160) — № 17
(7, 24, 25) = (11753, -10296, 16800) — №25
(21, 20, 29) = (15939, 18460, 48720) — № 46
(9, 40, 41) = (42471, -54280, 59040) — № 51
(11,60,61) = (117469, -194220, 161040) — №87
и т.д.
Примечание 2. Математики знают, что эйлеровы кирпичи всегда появляются парами. Существуют строгие математические доказательства того, что это происходит так и только так, хотя лично для меня (с моей колокольни:) это просто очевидно. Например, для кирпича (117, 44, 240) — №1 парой является (429, 2340, 880) — № 10. Параметрическая формула никогда не включает в себя оба парных кирпича.
Друзья! Я отыскал вторую параметрическую формулу! Собственно, это открытие! Этого не было 200 с лишним лет!!! Любой математик может быстро удостовериться в ее истинности.
Несколько примеров. В первых скобках целочисленная пифагорова тройка, во вторых скобках — эйлеров кирпич, полученный по параметрической формуле №2, потом номер в «грамотно составленном списке».
(3, 4, 5) = (275, 252, 240) — №2
(5, 12, 13) = (-4901, 13860, -4368) — № 23
(15, 8, 17) = (98549, -16380, 62832) — № 65
(7, 24, 25) = (-171875, 157500, -150000) — … таких значений в списке нет, но, если разделить все числа на 625 получим (-275, 252, -240) — двоюродный брат №2. См. Примечание №3.
(21, 20, 29) = (564311, 128520, 459360) — № 176
(9, 40, 41) = (-1645699, 933660, -1407120) — № 300
(11,60,61) = (-9261569, 3825360, -7788480) — № 686
(33, 56, 65) = (3063125, 8662500, 2730000) — .. таких значений в списке нет, но, если разделить все числа на 625 получим (4901, 13860, 4368) — двоюродный брат №23. См. Примечание №3.
… и т.д.
Как бы классическая формулировка Задачи о кирпичах Эйлера, гласит: существует ли идеальный кирпич, в котором еще и центральная диагональ является целой? Я считаю, что тут математики просто расписались в собственном бессилии. Казалось бы, прежде чем браться за четвертую диагональ, опишите для начала предыдущие три, верно? Они, эти математики, чтобы отвлечь внимание, подсунули миру теорему Ферма, эту извращенную форму геометрических соотношений. Эйлер отмахнулся от нее, как от назойливой мухи, сказав, что он и сам может таких формул написать хоть тысячу, и вы не сможете доказать ни их истинность, ни ложность. Кстати, лично я, для степеней кратных 4, доказываю ее «на пальцах». В отличие от теоремы Ферма, кирпичи Эйлера напрямую связаны с геометрией нашего мира.
Полагаю, предоставленной здесь информации вполне достаточно, чтобы при небольшом везении и внимании Вы и сами смогли написать еще несколько формул или даже вывести какой-нибудь общий принцип, если, конечно, Вам будет это интересно.
Также этот материал опубликован на моем сайте
http://eulerbricks.ru/zapis-2-kirpichi-eulera/
С уважением, Игорь И.
Сравнения по модулю для задач на делимость
С ужасом обнаружил, что на пикабу нет статьи про такую прекрасную вещь, как сравнения по модулю и их применение в решении задач на делимость. А тем временем школьники страдают от сложности задачи "Найти, при каких натуральных n выражение n^4 + n^3 + n^2 + 2 делится на 4 без остатка или показать, что таких нет". Вне всяких сомнений особо шустрые школьники решат эту задачу, но сколько на это уйдёт времени? Я же предлагаю использовать метод сравнений по модулю, который в сущности своей довольно прост. В конце мы режим и эту задачу. Кстати, кажется, он может пригодиться даже на ЕГЭ. Итак.
Вспомним несколько простых фактов о делимости в Z. Собственно, иную и не рассматриваем. Поделить a на b (условимся рассматривать только целые числа) означает представить a как
a = bk + r, где r - остаток. На него накладываются определённые условия:
0 =< r < |b|. Важно запомнить, что остаток не может быть отрицательным, так что -9 равно не 4*(-2) - 1, а 4*(-3) + 3. Далее, при последовательном делении чисел на m получается m остатков со значениями 0, 1, ..., m - 1. Это всё простые вещи. Теперь новшества.
Два числа a и b называются сравнимыми по модулю m, если их разность нацело делится на m = два числа a и b называются сравнимыми по модулю m, если при делении на m они дают одинаковы остаток = два числа a и b называются сравнимыми по модулю m, если a = b + mk. Пишется это так:
a ≡ b (mod m)
Что там с примерами? Уже готовы.
7 ≡ 1 (mod 3)
12 ≡ 2 (mod 10)
4 ≡ -1 (mod 5)
Ну и зачем это? Сейчас всё будет. Для начала покажем некоторые свойства сравнений по модулю:
1. a ≡ a (mod m)
Док-во:
a - a = 0 - делится на m.
2. Если a ≡ b (mod m), а b ≡ c (mod m), то a ≡ c (mod m)
Док-во:
Если a ≡ b (mod m), то они дают при делении на m некий одинаковый остаток z. Из b ≡ c (mod m) следует, что c при делении на m даёт тот же остаток z. Отсюда уже по определению следует сравнимость a и c по модулю m.
3. Если a ≡ b (mod m), а c ≡ d (mod m), то a + c ≡ b + d (mod m)
Док-во:
Сами докажите и не забудьте ещё про разность. Мне лень. :)
4. Если a ≡ b (mod m), то ah ≡ bh (mod m), где h - целое число.
Док-во:
Из сравнимости следует, что
a - b = mk
Домножим обе части на целое число h
ah - bh = mkh
Вот тут можно как перейти к модулю mh, так и остаться в модуле m. Мы останемся, так что воспользуемся ассоциативностью умножения в кольце (Z, +, *) и очевидной замкнутостью относительно * (это, впрочем, следует из определения кольца):
ah - bh = m(kh)
ah - bh = mg, где g = kh - целое число
Итак, мы получили, что ah - bh делится на m с нулевым остатком. Следовательно?..
5. Если a ≡ b (mod m), то a^n ≡ b^n (mod m), где n - натуральное число.
Док-во:
Так хочется полежать...
6. Ну тут сами или загляните в википедию. Я и так написал слишком много, чтобы изобрести уже два велосипеда. Вы совершенно справедливо заметите, если скажете, мол, хватит нам пудрить мозги - давай уже за дело. Даю...
Но! Сперва я введу ещё одну структуру - класс вычетов по модулю m. Чтобы объяснить взаимозаменяемость, которой мы позже коснёмся. :)
Будем последовательно делить на m, отвлекаясь от неполного/полного частного. Нас интересуют только остатки от деления. Скажем, будем последовательно делить на 4 (из дидактических соображений не увожу в область отрицательных чисел) и искать значение числовой функции Rest, которая выдаёт остатки от деления:
Rest(0; 4) = 0
Rest(1; 4) = 1
Rest(2; 4) = 2
Rest(3; 4) = 3
Rest(4; 4) = 0
Rest(5; 4) = 1
Rest(6; 4) = 2
Rest(7;4) = 3
...
Далее получится 0 и снова будут повторяться остатки. Цикл замкнулся. Далее заметим, что числа с равными остатками в общем виде представимы как a = 4k + r, где r принадлежит множество {0, 1, 2, 3} [ мы берём модуль 4, то есть делим на 4]. Эти числа разбивают всё множество Z на определённые группы чисел, которые имеют одинаковые остатки при делении на 4. Обобщим это на любой модуль m: последовательное деление на m разбивает множество Z на классы чисел, дающие при делении на m одинаковый остаток. Эти числа, очевидно, сравнимы по модулю m. Такие классы называются классами вычетов по модулю m. Их всего будет m штук. Множество классов вычетов по модулю m обозначается как G(m). Образуем, примера ради, множество G(2). Итак, всего будет 2 класса вычетов, причём они будут сравнимы по модулю 2 с числам 0 и 1. Если обозначить класс вычетов по модулю m как [k], где k - наименьший положительный вычет, то получатся два класса:
[0] = {2l}
[1] = {2l + 1}
Тогда G(2) = {[0], [1]}
Таким образом классы вычетов суть множества (классы, если точнее). Зачем они нам? В нашем случае - на самом деле это очень богатая структура - они позволяют взаимозаменять числа, сравнимые по модулю m, ибо тогда они попадут в один класс вычетов по модулю m. Иными словами, все числа из одного класса вычетов по модулю m тождественны при решении задач на остатки. Вот теперь мы готовы к задачам.
1. При каких натуральных n выражение n^2 + 2 делится на 2 без остатка?
Решение:
Переформулируем задачу на языке сравнений по модулю 2:
n^2 + 2 ≡ 0 (mod 2)
Будем смотреть на n в упор, для которого существует всего два случая:
1. n ≡ 0 (mod 2)
Далее возводим в квадрат обе части сравнения:
n^2 ≡ 0 (mod 2)
И прибавляем 2:
n^2 + 2 ≡ 0 (mod 2)
Многие здесь недоумевают, почему n^2 + 2 ≡ 0 (mod 2), а не n^2 + 2 ≡ 0 (mod 2). На самом деле всё просто: прибавляя к обеим частям число вида ml, где m - модуль сравнения, правая или левая часть не меняется, "счётчик обнуляется" (подумайте почему, см. остатки и определение сравнения).
2. n ≡ 1 (mod 2)
n^2 ≡ 1 (mod 2)
n^2 + 2 ≡ 1 (mod 2)
Итак, наше требование выполняется только при n ≡ 0 (mod 2), то есть n = 2k -чётном натуральном числе. Записывайте ответ.
2. Доказать, что a^n + b^n, где n - натуральное число, делится на a - b без остатка.
Решение:
Нужно доказать, что a^n + b^n ≡ 0 (mod a - b)
Давайте с галёрки:
a ≡ b (mod a - b) - проверьте!
a^n ≡ b ^n (mod a - b)
a^n - b^n ≡ 0 (mod a - b)
ЧТД.
3. Найти последнюю цифру 17^2132
Решение:
Нас просят найти x с условием 17^2132 ≡ x (mod 10)
Идём с галёрки:
17^2132 ≡ 7^2132 [помните про классы вычетов???] (mod 10)
Далее замечаем 7^4 = 2401 ≡ 1 (mod 10)
7^2132 = (7^4)^533 ≡ 1^533 = 1 (mod 10)
Итак, последняя цифра 1.
4. Решим предложенную в самом начале задачу.
Решение:
Нам нужно рассмотреть 4 случая и вытащить 4 сравнения.
1)
n ≡ 0 (mod 4)
n^2 ≡ 0 (mod 4)
n^3 ≡ 0 (mod 4)
n^4 ≡ 0 (mod 4)
n^4 + n^3 + n^2 + n ≡ 0 (mod 4) - сложили сравнения
n^4 + n^3 + n^2 + n + 2 ≡ 2 (mod 4) - не подходит: остаток 2
2)
...
Ну, вы поняли! :)
Пусть это будет домашним заданием, а я на этом заканчиваю. Вот.