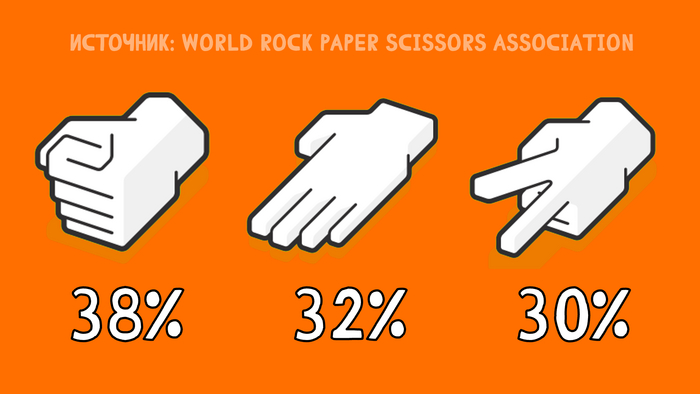
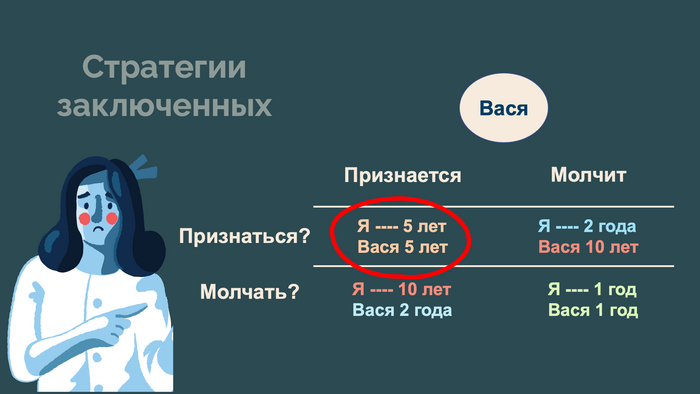
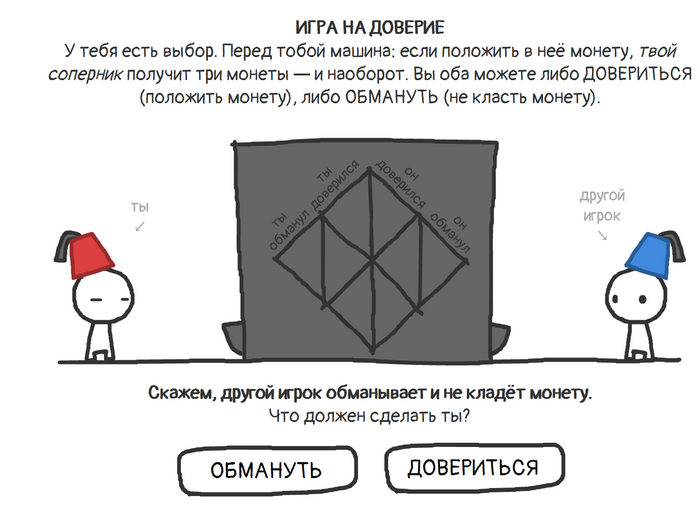
Термин из Словаря по конфликтологии С.М. Храмова
О ТЕОРИИ ИГР ОДНОЙ СТРОЧКОЙ: это инструменты для анализа конфликтов.
Теория игр изучает формальные модели принятия решений в условиях конфликта.
Это математический метод, который позволяет проанализировать ситуацию и выбрать оптимальную стратегию поведения в конфликте, объяснить или изменить человеческое поведение.
Теория игр является общепризнанным инструментом консультирования и прогнозирования.
«Становлению теории принятия решений во многом содействовали в качестве изобретателей теории игр Е. Борель (1871-1956) и Дж. фон Нейман (1903-1957)».
Источник — портал VIKENT.RU: https://vikent.ru/enc/5746/
«Фактически, теория игр была первоначально разработана американским математиком венгерского происхождения Джоном фон Нейманом и его коллегой из Принстонского университета Оскаром Моргенштерном, американским экономистом немецкого происхождения, для решения экономических проблем.
В своей книге „Теория игр и экономического поведения“ (1944) фон Нейман и Моргенштерн [...] заметили, что экономика во многом похожа на игру, в которой игроки предвосхищают ходы друг друга, и поэтому требует нового вида математики, которую они назвали теорией игр. (Название может быть несколько неправильным — теория игр обычно не разделяет веселья или легкомыслия, связанного с играми)».
Game theory (пер. с англ). URL: https://www.britannica.com/science/game-theory (дата обращения: 29.08.2021).
«Томас Шеллинг использовал теорию игр, которая дает возможность принятия рациональных решений в условиях дефицита информации. Его базовым трудом стала «Стратегия конфликта», опубликованная в пятидесятые годы прошлого века. В своей книге Шеллинг показывает, НАПРИМЕР, что способность принять ответные меры может быть иногда более полезной, чем способность выдержать атаку, или что «возможное неизвестное возмездие часто более эффективно, нежели известное неотвратимое возмездие».
Велетминский И. Доигрались. Нобелевская премия в области экономики присуждена двум ученым за теорию игр // Российская газета — Столичный выпуск № 0(3896). 2005. 11 окт. URL: https://rg.ru/2005/10/11/nobel.html (дата обращения: 29.08.2021).
В 1994 году за исследования в области теории игр Нобелевская премия по экономике была вручена американскому математику Джону Нэшу, специализировавшемуся на стратегическом моделировании.
Ричард Даффин — преподаватель Нэша в Политехническом институте Карнеги — называл своего ученика гением математики.
Д. Нэш являлся прототипом главного героя фильма «Игры разума» (США, 2001 г.).
Этот фильм удостоен четырех Оскаров.
Исследователь исходил из того, что есть разные люди. У каждого свой набор действий. В итоге сочетание таких действий приводит к определенному результату.
Д. Нэш придумал общий способ определять равновесие в конфликтной ситуации.
Равновесие по Нэшу — такая ситуация, когда человек ожидает определенное поведение других людей и в связи с этим не меняет свое действие.
Иллюстрирующий пример равновесия
Вы едете по своей стороне улицы на автомашине, а не по противоположной стороне = участвуете в равновесии по Нэшу.
Алгоритм поиска равновесия по Нэшу
1. Разложить ситуации на составляющие.
2. Осуществить поиск равновесия.
Наличие неопределенности и дефицита информации в условии решаемой задачи не является препятствием для применения теории игр.
Теория игр «создает условия, в которых участники играют друг против друга, получая различные награды в зависимости от своего поведения, и пытаются понять, когда выгоднее сотрудничать, а когда подставить.
[...] первой беспроигрышной стратегией считалась стратегия под названием „Зуб за зуб“. Вы начинаете с сотрудничества. Как только вас подставляют, вы в следующем круге платите обидчику той же монетой. Если оппонент решает возобновить сотрудничество, вы делаете то же самое.
Однако всегда есть вероятность ошибки. По какой-то причине игрок, который сотрудничает, может показаться партнёру обманщиком.
[...] стратегия „зуб за зуб“ допускает возможность ошибки и оказывается, она не так уж хороша. Поэтому новой „беспроигрышной“ стратегией назвали стратегию „прощения“. Она заключается в том, что один из игроков поступается своими принципами и прощает предательство, чтобы восстановить сотрудничество. Однако вскоре выяснилось, что и эта стратегия имеет свою уязвимость — „прощающего“ легко использовать».
Конспект лекции профессор биологии Стэнфордского университета Роберта Сапольского «Поведенческая эволюция. Достаточно лишь сравнить размеры самцов и самок, чтобы понять социальное устройство внутри вида» // Наука и жизнь. 2021. № 8. URL: https://www.nkj.ru/open/36341/ (дата обращения: 29.08.2021).
При конфликте затрагиваются интересы двух или более сторон.
Варианты возможных интересов игроков
— схожие интересы,
— противоположные интересы,
— смешанные интересы.
Классификация игр
А) По количеству игроков:
— игра для одного человека,
Пример игры для одного человека: человек, решающий, брать с собой на улицу зонт или нет.
— игра для двух человек,
— игра для N человек (где N — больше двух).
Б) По степени совпадения или противоречия целей игроков:
— некооперативные игры с нулевой суммой (у сторон конфликта интересы полностью противоположны, выигрыш одного игрока = проигрышу другого),
— кооперативные (коалиционные) и некооперативные игры с ненулевой суммой (у сторон есть как общие, так и противоположные интересы).
Неформальные обозначения антагонистических игр: «игра в цыпленка» (game of chicken), «ястребы и голуби» (hawks and doves), и описывается в реалиях русского языка как «брать на слабо/кто струсит первым».
Цель подобной игры-противостояния — заставить другого игрока сдать позиции первым под психологическим давлением и получить весь выигрыш«.
Вильданова Г.А., Кожухова И. В. Коммуникативные ресурсы антагонистической игры в современном американском политическом дискурсе // Вестник ТГПУ (TSPU Bulletin). 2019. 9 (206). С. 85.
Элементом реализации стратегий с нулевой суммой могут быть публикации в СМИ.
Пример. «Особой популярностью пользуются токсичные посты Д. Трампа в „Твиттере“, изобилующие оскорбительными ярлыками и пропитанные агрессивной риторикой в адрес неугодных политику личностей».
Вильданова Г.А., Кожухова И. В. Коммуникативные ресурсы антагонистической игры в современном американском политическом дискурсе // Вестник ТГПУ (TSPU Bulletin). 2019. 9 (206). С. 87.
Теория безумца
Суть стратегической «теории безумца» «состоит в устрашении противника путем внушения ему мысли, что у власти находится неадекватный человек, способный на крайние меры, в том числе на применение ядерного оружия. Р. Никсон применял „стратегию безумца“ для давления на Советский Союз во время войны во Вьетнаме, однако в целом данная концепция показала себя неэффективной».
Вильданова Г.А., Кожухова И. В. Коммуникативные ресурсы антагонистической игры в современном американском политическом дискурсе // Вестник ТГПУ (TSPU Bulletin). 2019. 9 (206). С. 88.
При реализации среднесрочных стратегий целесообразно применять игры с ненулевой суммой.
Описание пункта «Б» классификации игр в методической литературе
«В теории игр выделяются два класса:
1) игры со строгим соперничеством (или, что равнозначно, с нулевой суммой), когда два игрока имеют прямо противоположные интересы: один выигрывает столько, сколько проигрывает другой;
2) игры с нестрогим соперничеством (или с ненулевой суммой), где возможен обоюдный выигрыш.
Игры с ненулевой суммой, предоставляющие возможность как конкурентного, так и кооперативного поведения сторон, как раз и были избраны моделью для изучения конфликтного взаимодействия и определяющих его факторов».
Полозова Т.А. Методические проблемы изучения межличностного конфликта в группе. 1980. № 4. С. 124.
Пример игры для двух человек с нулевой суммой
Шахматы, в которых возможно только три исхода — белые выигрывают, черные выигрывают, ничья.
Примеры игры для двух человек с ненулевой суммой
1. Покупатель хочет более низкую цену за товар, а продавец — более высокую. Вместе с тем, оба в итоге хотят заключить сделку.
2. Два конкурента могут не соглашаться по поводу многочисленных проблемы, но оба выигрывают, если избегают прямой конфронтации.
3. Два пилота, пытающиеся избежать столкновения в воздухе. Оба пилота выиграют, если между ними есть канал общения.
Окончание статьи будет опубликовано 13 апреля 2022 года
+ Ваши дополнительные возможности:
Видео: ЭНЦИКЛОПЕДИЯ / СЛОВАРЬ ТВОРЧЕСТВА VIKENT.RU: Стратегии личности