Легкая магия расчета мощности и крутящего момента
Умение быстро что-нибудь посчитать — это не только приятный навык, но и приносящий практическую пользу инструмент. В этом смысле было бы не плохо иметь способность быстро оценить мощность и крутящий момент ДВС в реальных дорожных ситуациях.
Надо сказать, что мощность двигателя невозможно измерить напрямую по причине непонимания природы столь загадочного и не изученного явления как энергия. Обычно измеряют более «реальный» параметр, а мощность рассчитывают как функцию от измеренного аргумента через известные соотношения. Крутящий момент — это более «реальный» параметр, и вот его уже вполне можно измерять разными способами, например на динамометрическом стенде. Вывести формулу соотношения мощности и крутящего момента не сложно. Для этого нужно вспомнить несколько формул из курса школьной физики. Если нет желания вникать в элементарную физику, можете пролистать дальнейшее изложение до конечного результата — формулы (8). Итак.
Мощность — это скорость преобразования энергии, или проще говоря, количество потраченной энергии за единицу времени:
P = E : t (1)
где: P — мощность в ваттах
E — энергия в джоулях
t — время в секундах
Энергия — это универсальный источник движения, определяемый произведением силы на длину поступательного пути:
E = F · L (2)
где: E — энергия в джоулях
F — сила в ньютонах
L — путь в метрах
Крутящий момент — это усилие, вызывающее вращение вокруг оси, или другими словами, произведение силы на радиус приложения этой силы:
M = F · R (3)
где: M — крутящий момент в ньютон·метрах
F — сила в ньютонах
R — радиус в метрах
А еще нам понадобится длина окружности:
2π·R (4)
Начнем с момента, указанного в формуле (3). ДВС на выходном валу создает некоторое усилие (F), приложенное к радиусу (R), в результате чего точка приложения силы движется по окружности длиной 2πR. Значит, используя формулу (2), можем посчитать количество энергии, затраченной на один оборот вала:
E = (2π · R · F) (5)
Двигатель вращает выходной вал с частотой (n) оборотов в минуту. Значит за все (n) оборотов потратится в (n) раз больше энергии:
E = (2π · R · F · n) (6)
Из формулы (1) видно, что мощность рассчитывается в киловаттах и секундных интервалах, а не в ваттах и минутных. Учтем это в формуле:
P` = (2π · R · F · n) : (60 · 1000) (7)
Помня, что R * F — это крутящий момент, мы готовы написать соотношение мощности и крутящего момента:
Pkv = (M · n) : 9549 (8)
где: Pkv — мощность в киловаттах
M — крутящий момент в ньютон·метрах
n — обороты в минуту
Мощность ДВС часто характеризуют в лошадиных силах, а коэффициент пересчета киловатт в лошадиные силы в России принимают равным 1,36. Скорректируем константу с учетом этого коэффициента:
Php = Pkv · 1,36 = (M · n) : 7023 (9)
где: Php — мощность в лошадиных силах
M — крутящий момент в ньютон·метрах
n — обороты в минуту
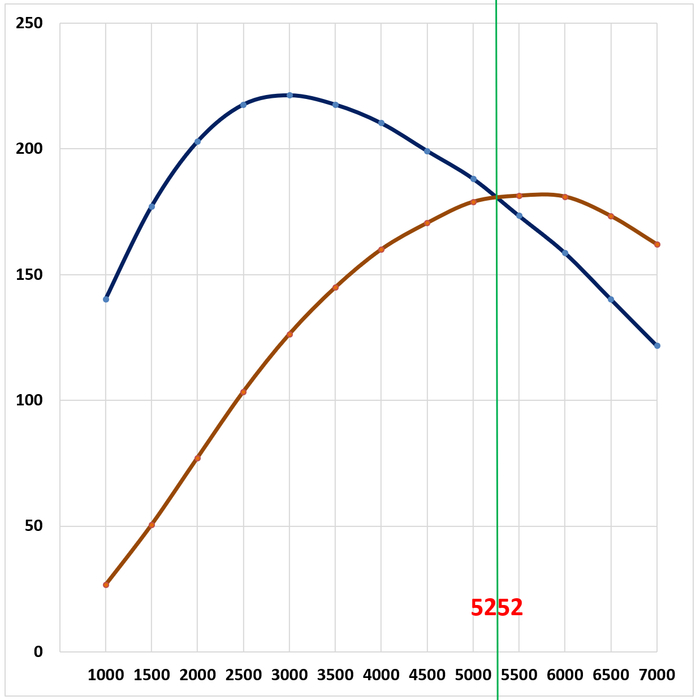
Здесь необходимо упомянуть об автомобильной отрасли США и Великобритании. Местные автопроизводители считают одну лошадиную силу как 746 Ватт, а крутящий момент измеряют в фунто-футах. В этой системе координат константа будет равна 5252. Особенностью константы в таком расчете является то, что она фактически указывает на точку пересечения мощности и крутящего момента. При частоте вращения вала 5252 оборота в минуту числовые значения крутящего момента (в фунто-футах) и мощности (в американских лошадиных силах) совпадают, а их кривые на графике пересекаются. Левее этой точки доминирует крутящий момент, а правее — мощность.
Мы вывели формулу соотношения Мощности, Крутящего момента и Оборотов ДВС. Теперь можно применить эти знания для расчета реальной ситуации на дороге. Вот пример такого расчета. Представим себе, что мы сидим в автомобиле общей массой 1,8 тонны. Автомобиль с равномерной скоростью взбирается вверх по горной дороге с наклоном 20°. ДВС надрывно гудит, а тахометр показывает устойчивые 2200 оборотов в минуту. Попробуем посчитать крутящий момент и мощность ДВС.
Из условий понятно, что мотору нужно преодолевать действие земной гравитации, стремящейся скатить автомобиль вниз по склону. Каково это гравитационное усилие? Оно пропорционально весу авто (1800кг), ускорению земной гравитации (9,8м/с2) и синусу угла наклона (20°):
1800 · 9,8 · SIN(20°) = 6033 Ньютона (10)
Опустим пока потери на трение и посчитаем, какой крутящий момент должны развивать колеса радиусом 36 см, чтобы противостоять гравитационному усилию (6033Н):
0,36 · 6033 = 2172 Ньютон·метра (11)
Между выходным валом ДВС и колёсами расположены несколько агрегатов. Нас интересует коробка передач с включенной второй передачей и главная передача в раздатке. Пусть их передаточные числа будут равняться соответственно 2,8 и 4. Тогда крутящий момент на валу ДВС составит:
2172 ∶ (2,8 · 4) = 194 Ньютон·метра (12)
Зная крутящий момент на валу ДВС (194Нм), обороты двигателя (2200мин-1), и пользуясь формулой (9), посчитаем текущую мощность нашего ДВС:
(194 · 2200) ∶ 7023 = 61 лошадиная сила (13)
Мы не учли потери на трение в узлах двигателя, трансмиссии и колес. Давайте оценим их в 10%:
194 · 110% = 213 Ньютон·метров (14)
61 · 110% = 67 лошадиных сил (15)
Если верить расчетным значениям, то у нас под капотом дизель, но это не точно. В качестве бонуса посчитаем скорость движения нашего авто на подъеме в горку. Нам понадобятся обороты двигателя (2200м-1), радиус колес (36см) и передаточные числа агрегатов трансмиссии (2,8) и (4):
(2200 · 2π · 0,36) ∶ (2,8 · 4) = 444 м/мин (27 км/ч) (16)
Благодарю вас, если дочитали до этого места. И последнее. Вопреки расхожему мнению, паспортная мощность двигателя не является технической характеристикой ДВС в том смысле, что не может рассматриваться как непосредственная характеристика силового агрегата. Но это тема для другой статьи.