Парадокс Рассела и его влияние на математический мир
В этом посте я написал о парадоксах и предложил некоторое деление их на категории. Сегодня напишу об ещё одном парадоксе, а именно парадокс Рассела или парадокс брадобрея. Одна из формулировок звучит так:
В деревне живет брадобрей, который бреет всех, кто сам себя не бреет, и только их. Бреет ли брадобрей сам себя? (спасибо @Naigur, за корректировку)
И далее если он себя бреет, то брить не должен, а если не бреет, то наоборот должен брить. Данный парадокс является ложным в такой формулировке или, если немного подправить, псевдопарадоксом.
Но об этом чуть ниже. А для начала небольшой исторический экскурс. В свое время Евклид написал 5 аксиом своей геометрии:
От всякой точки до всякой точки можно провести прямую линию.
Ограниченную прямую можно непрерывно продолжать по прямой.
Из всякого центра всяким радиусом может быть описан круг.
Все прямые углы равны между собой.
Если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых углов, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых углов.
Пятый постулат можно заменить другим утверждением, более привычным нам. А именно, что
5*. Через любую точку на плоскости можно провести ровно одну прямую, параллельную другой.
Однако возникал естественный вопрос: не следует ли аксиома 5 из предыдущих? Ответ был дан Лобачевским как известно. Но это не совсем так. Сферическую геометрию знали и до открытия Лобачевского. Но куда важнее был, во-первых, сам подход к определению независимости аксиоматики. Для этого было построенное две геометрии с 5й аксиомой и её отрицанием. И во-вторых, стало понятно, что нужно развивать аксиоматику.
Первую формальную геометрию построил Гильберт, хотя попытки были и после него. Он же продвигал идею о полной формализации математики. Кантор вместе с Дедекиндом пытались строить формальную теорию множеств. Классически сейчас говорят, что она противоречиво, но есть и обратные мнения. Я с работами Кантора не знаком, возможно, историкам математики может быть интересно с этим покопаться. А точнее, есть утверждение, которое называется аксиома Фреге. А именно, что для любой логической формулы f существует множество { x | f(x)}. Эта аксиома слишком сильная и приводит к противоречию. Например, если в качестве f взять тождественную истинную формулу, то получится множество всех множеств. Но такого множества не существует.
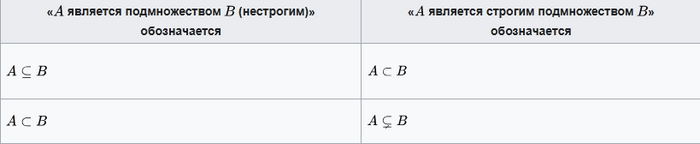
Действительно, пусть это не так и множество всех множеств U существует. В частности, U тоже лежит в U. Тогда рассмотрим множество Q всех таких Y из U, что Y не лежит в Y. Q это множество. Тогда если Q не лежит в Q, то Q лежит в Q и наоборот. Надеюсь, вы увидели рассуждения, похожие на брадобрейские. Собственно, в классической теории множеств (ZF и ZFC) отказались от этого утверждения, заменив его более слабой версией аксиомы выделения (на самом деле, это схема аксиом, их там много). В ней, если говорить грубо, запрещается делать проверки по всем множествам, как это в аксиоме Фреге, а только по уже полученным множествам.
В парадоксе брадобрея, описанном мной, сказано две вещи. Во-первых, что брадобрей существует и, во-вторых, что он обладает указанным свойством. Свойство противоречиво, то есть его можно заменить на условие "такого брадобрея не существует". И тогда сразу понятно, что утверждения X и ¬X не могут одновременно выполнятся и отсюда парадокс. Или, если убрать требование к тому, что брадобрей существует, то получим что множество брадобреев пусто. А, как известно, элементы пустого множества обладают любым свойством (формула, которая имеет вид "∀х ∈ ∅ Ф" для любой формулы Ф, истина).