Интернет переполнен спекуляциями по поводу Египетских пирамид. «Очень трудно найти черную кошку в темной комнате, особенно, если ее там нет» - это я по поводу «Золотого сечения» в пирамиде Хеопса. Однако есть вопросы: стоит ли тратить время, чтобы бороться с ересью? В ситуации, когда тысячи человек «ведутся» на мистику новоявленных отечественных и западных «гуру», следую совету Э.М.Ремарка: надо, пусть хоть одним навязанным заблуждением станет меньше в представлениях хотя бы нескольких человек. Надеюсь, что опровержение ложных суеверий не может быть истолковано как унижение человеческого достоинства.
Если «погуглить» Интернет [ https://www.google.ru/ ] с ключевыми словами: пирамида Хеопса «золотое сечение» - то будет найдено около 16600 результатов. Открыв первый попавшийся: http://www.phantomgallery.64g.ru/pyramid/pyr2.htm , я удивлялся фразам типа: «…я не могу утверждать, что строители зашифровали идеальную фигуру человека и формы семиугольника в архитектуре египетских пирамидальных конструкций, но такие пропорции являются очевидными»
- обожаю внутренне противоречивые высказывания.
А также: «По-видимому, разные пирамиды были вычислены строителями в результате разных трансформаций и преобразований линий бигептагональной геометрической сети в пространстве эллипса живой окружности»
- они их не вычисляли, а просто строили. Но каков стиль и термины!
А также: «Показанные геометрические чертежи являются приблизительными, поскольку для точных вычислений необходимо множество чисел и математических формул, что нецелесообразно в контексте художественной галереи фантомных изображений, но согласно показанным чертежам можно делать точные геометрические вычисления, если это необходимо с точки зрения научных исследований эзотерических принципов мировой гармонии, или с точки зрения математических решений иных задач в науке или архитектуре, или…».
- «множество чисел», определяющих «правильную» пирамиду - это два числа: ширина основания и высота. «Множество формул» - оно ниже, и занимает полстрочки.
Зачем в методике доказательства «Золотого сечения» в пирамиде пытаться применить
семиугольник, а не на пятиконечную звезду, в которой сплошь «Золотые сечения»? В статье, посвященной понятию «Золотое сечение» 9 раз употребляется слово «приблизительно». С какой стати абсолютное понятие может быть «приближенным»? Оно либо есть, либо его нет. Впрочем, адрес статьи указан выше, желающие могут в полной мере насладиться «крутизной» автора, а нам пора переходить к существу вопроса.
Не только в цитируемой статье, но и в других источниках можно найти два утверждения, противоречащие друг другу и эквивалентные следующим.
1. Если высоту пирамиды принять за единицу длины (1) (сколько в ней метров, или локтей не важно) то ширина ее основания равна pi/2. (т.е. периметр равен 2*pi )
2. Отношение высоты боковой грани пирамиды (равнобедренного треугольника) к полуширине ее основания (pi/4) равно "Золотому сечению".
Имея даже неполное среднее образование нетрудно заметить: будь эти утверждения верными одновременно, не было бы проблемы, называющейся "Квадратура круга". Некоторые так прямо и пишут, что древним египтянам удалось решить задачу «о квадратуре круга»… Напомню: "Золотое сечение" строится на основе прямоугольного треугольника с катетами 1 и 2.
Начнем с второго утверждения, проверим его численно. Используя теорему Пифагора при вычислении высоты боковой грани и решение квадратного уравнения для "Золотого сечения", получим:
sqrt((pi/4)^2+1) / (pi/4) - (sqrt(5) - 1) / 2 = 0,000959198 (Снятие "тайны" пирамид в полстрочки!)
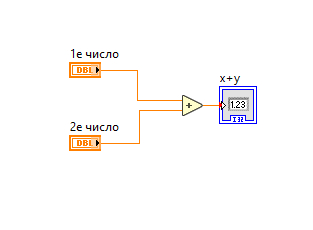
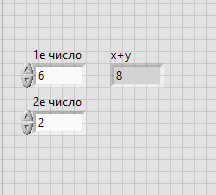
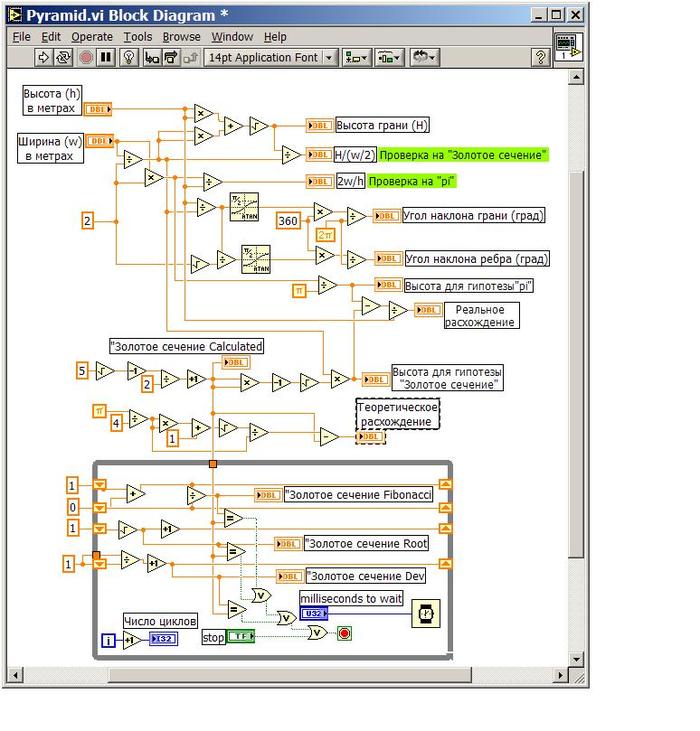
Да, разница небольшая, но это всего лишь арифметический факт, и не более того! Кстати, не так уж и близки эти два значения. Для сравнения: при вычислении «Золотого сечения» четырьмя различными способами, включая 3 его рекурсивные формулы, уже после 32-х итераций обеспечивается точность совпадения не менее 12 знаков для всех четырех методов: 1.61803398875. Иными словами, даже приближенные рекурсивные вычисления дают ошибку в 200 миллионов раз меньше полученной выше разности. Соответствующие вычисления методом графического программирования на основе LabVIEW приводятся на прилагаемых рисунках.
А вот как просто практически привнести в строительство пирамиды число pi, даже не зная его. Известно, что поперечное сечение камней соответствовало эталону, размером в 2 локтя, т.е. он же определяет высоту очередной ступени пирамиды (о «локте» и таком эталоне см. ниже). Представим себе другой эталон – ширину ступени - длину дуги одного квадранта окружности, радиусом один локоть. Известно, что «спрямление окружности» они умели делать, прокатывая цилиндр по плоскости. На это расстояние следует отступить от края при укладке очередного слоя пирамиды. Надежность конструкции будет обеспечена, т.к. продольная щель между камнями нижнего слоя перекрывается верхним слоем камней, поскольку pi/4 меньше единицы.
Это все! Далее никаких расчетов не требуется: высота самой пирамиды, высота боковых граней (равнобедренных треугольников) углы наклона граней и ребер - все это «вторично», т.е. само собой получится. Отношение между шириной основания и высотой, кратное числу pi, также получится само собой, никакой «эзотерики» здесь нет. Более того, абсолютно не имеет значения, чему равен этот самый «локоть». В процессе строительства можно даже перейти на другой размер локтя. На высоту пирамиды это не повлияет, если делать замену эталонов одновременно и между слоями. Известно, что в процессе строительства это делалось неоднократно. Какое количество слоев при этом будет – совершенно не важно – ровно столько, сколько нужно для схождения ребер в вершине, разумеется, с учетом облицовки.
Уже сказано, что два утверждения, приведенные выше, не могут быть верными одновременно, но альтернативная технология строительства на основе «Золотого сечения» как гипотеза должна быть рассмотрена, раз уж она заявлена. Для ее обоснования много чего маловероятного придется предположить. Сначала должно быть построено это самое «Золотое сечение», а по тем временам – это «Нечто» абстрактное, не представленное предметно в окружающем мире. И сразу вопрос: Как это «Нечто» может соперничать с круглым Солнцем, т.е. с самим богом Ра?! Да еще и «главный архитектор» пирамид, оказывается, был Хеси-Ра!
Некоторые могут возразить, мол, ряд Фибоначчи, порождающий «Золотое сечение», в природе также в определенной степени представлен. Даже если предположить совершенно невероятное, что они решились и смогли вычислить «Нечто» через ряд Фибоначчи, т.е. численно, то, что бы они потом делали с этим числом?
Другие могут настаивать: «Зато эталон №2 для гипотезы «Золотое сечение» не нуждается в «спрямлении окружности», а может быть построен теоретически, т.е. на плоскости с помощью циркуля и линейки». Тогда придется предположить, что древние египтяне могли работать с абстрактными величинами типа: А, В. Зачем-то составить из них пропорцию: A/B = (A+B)/A. Решить соответствующее квадратное уравнение. Получив ответ, в который входит квадратный корень из 5, построить его в виде отрезка прямой на основе эталона № 1, не зная теоремы Пифагора. Кстати, возможно, что именно Пифагор ввел позже термин «Египетский треугольник». Далее, допустим, что они это сечение все-таки получили, но в соответствии с гипотезой № 2 оно прилагается к надуманной нашими современниками высоте боковой грани пирамиды, которая, учитывая подобие треугольников, при геометрических построениях второго эталона эквивалентна расстоянию между ребрами соседних ступеней – гипотенузе, висящей в воздухе. Впрочем, имея один катет (эталон № 1) и гипотенузу, они смогли бы перейти ко второму эталону - ширине ступени. Вопрос самый простой: «Зачем все эти сложности»?
До сих пор мы рассматривали обе гипотезы теоретически, а теперь посмотрим какая из них ближе к размерам пирамиды, восстановленным нашими современниками, располагающими лазерным лучом. Итак: истинная высота пирамиды получается на 6,5 сантиметров выше, чем расчетная на основе гипотезы, что в пропорции пирамиды привнесено число “pi”, и на 20,5 см выше расчетной, при гипотезе: «использовано «Золотое сечение». Столь малые расхождения между истинными и расчетными размерами пирамиды, при ее гигантских размерах, конечно, удивляет, а вот разница между отклонениями, нормированная на высоту пирамиды – ожидаемо малая «практическая» величина, которая с высокой точностью соответствует расчету по теоретической формуле: «снятие тайны пирамид».
Теперь Читателю самому предоставляется возможность оценить вероятность гипотезы «Золотое сечение». Следует только напомнить, что с ростом величины отклонения ее вероятность убывает быстрее, чем экспоненциально, т.е. при сопоставлении гипотез имеем очень малую вероятность для «Золотого сечения» на основе одних только отклонений гипотетических расчетных значений от измеренной высоты. Эту вероятность еще следует умножить на вероятности всех предположений, названных выше. Оценить эти вероятности также предлагается самому Читателю…
Таким образом, они строили пирамиду, а не «Золотое сечение» и даже не число pi, которое привнесли в технологию строительства, выбрав величину сдвига камней, равной четверти «эталонной окружности», имеющей радиус, равный половине первого эталона. Нас же не удивит следующее: если на любом уровне измерить окружность «пузатой» деревянной бочки, сделанной нашими предками, и поделить на диаметр того же уровня, то всегда получится число pi, о чем бочар Гаврила даже не догадывался.
Теперь необходимо разобраться с «локтями» и эталонами, как было обещано. В цитируемой выше статье приводятся три варианта размера «локтей»: 466, 450 и 525 мм. Если ширина основания пирамиды была 500 локтей, как сказано там же, то размер локтя получается 460,7 мм, т.е. средний поперечный размер камня будет 921,4 мм. Так что в данном вопросе правильнее согласиться с другой гипотезой, будто размер поперечного сечения камней (эталон № 1) выбирался из «практических» соображений как обеспечивающий оптимальный баланс в трудозатратах на обработку поверхностей камней и их перетаскивание. Возможно, это были размеры «локтей» важных персон. И зачем они так часто меняли толщину слоев пирамиды? Однако этот вопрос к данной теме отношения не имеет.
Есть еще один повод обратиться к цитируемой выше статье. В ней имеется подсказка (без всякой иронии) по поводу эталона, а именно, фото полусгнившей резной деревянной доски, на которой, как утверждается, изображен архитектор пирамид Хеси-Ра с «тростью» в руке. Мне показалось, что на этом невнятном фото у «трости» есть какая-то «загогулина» на конце. Тут у остряков-самоучек сработает приобретенный инстинкт: «Когда кажется, нужно креститься». А мне подумалось: не могли же они при изображении столь важного предмета как эталон строительства довериться только такому недолговечному материалу как дерево. И нашел в полпинка на каком-то видео в Интернете такое же изображение в виде барельефа на камне. Некто держит эту самую «трость» в руке, и она представлена во всех подробностях. Так это же штангенциркуль! Подобно вырезам в углах примыкания губок к штанге у современного штангенциркуля верхний конец «трости» переходит в изгиб: в целом под прямым углом, но в форме знака тильда (~). Нижний конец раздвоенный, в форме большой буквы «омега» или ухвата (кому как больше нравится) а в середине овала имеется точка. Просто точка посередине дырки – явный указатель на то, что она-то как раз и важна при измерениях. А дальше – у кого насколько фантазии хватит, как этот инструмент использовался. Очевидно только, что зацепив камень «тильдой» с одной стороны, могли пропустить веревку через разрез «омеги» и осуществлять выравнивание, как по горизонтали, так и по вертикали (с помощью отвеса). Могли также использовать «омегу» как зажим для какого- то дополнительного простейшего устройства, позволяющего корректировать размер (подгоняя под очередной «локоть») или даже делать измерения. Нужно было только раздвоенные концы «омеги» затянуть бечевкой – они изогнуты должным образом, а в небольшом диапазоне медь пружинит. Словом, все приспособлено для практической работы, а не для «…трансформаций и преобразований линий бигептагональной геометрической сети в пространстве эллипса живой окружности».
Как-то видел еще одну интересную гипотезу: они могли катать камни. Любой нормальный человек через минуту может предложить «практическое» решение задачи, если ее правильно поставить: сделать дорогу для перекатывания камней квадратного сечения такую, чтобы центр тяжести камня во время движения перемещался по прямой (или его ось оставалась в одной плоскости). Получится дорога в виде последовательности бугров с глубиной впадин между ними, равной разности между половиной диагонали и половиной стороны квадрата. Длина огибающей бугра должна быть равна стороне квадрата.
Осталось добавить, что квадрат в основании пирамиды строился с ориентацией на Полярную звезду (что доказано) и прямого угла «египетского треугольника» (со сторонами 3, 4, 5) а горизонтальный уровень выставлялся по канаве с водой.
«Многие египтологи и исследователи пирамиды Хеопса предполагают, что строителям древнего Египта было известно числовое значение золотого сечения и число «пи» - там же. С такими «профессионалами» спорить не буду. Если ученый всю жизнь занимается изучением слона, и не пришел к выводу, что у слона есть хобот, то доказать ему это уже невозможно. На вопросы отвечу.