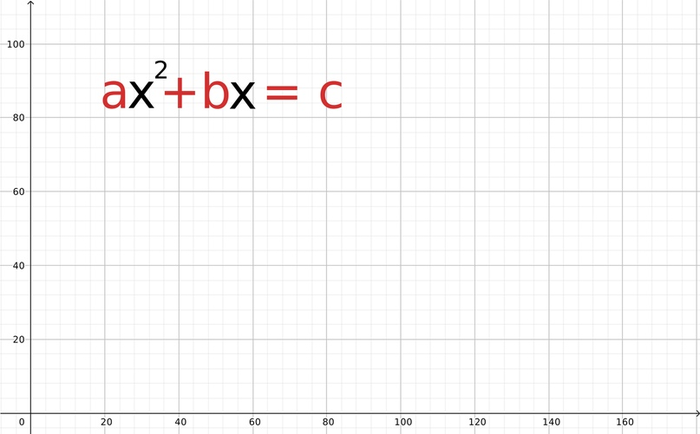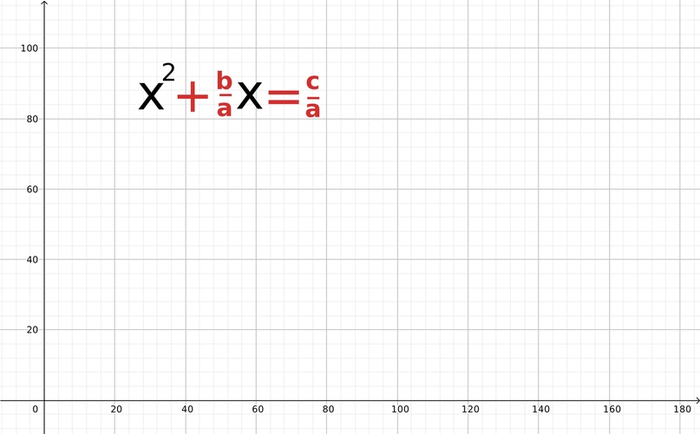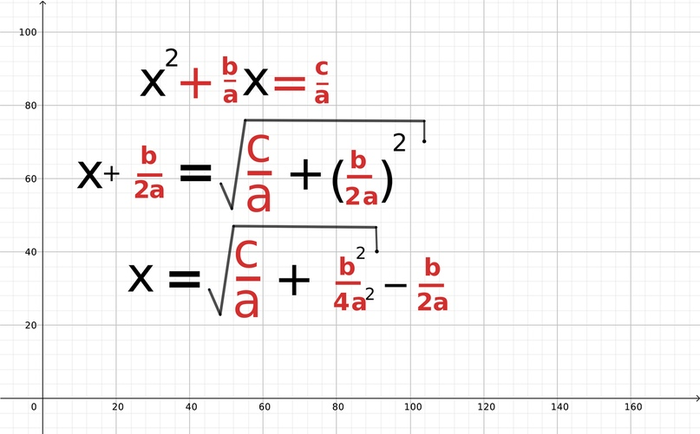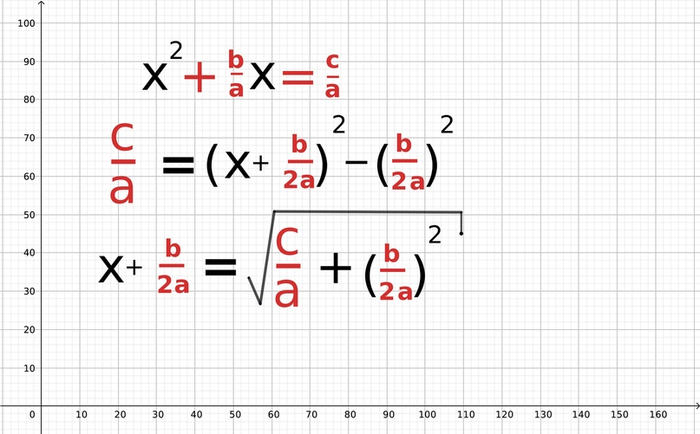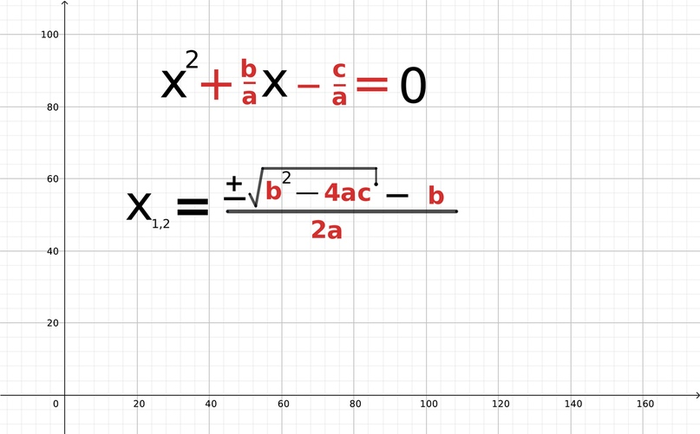0 просмотренных постов скрыто
Квадратные уравнения
В этом посте мы рассмотрим квадратные уравнения и способы их решения.
1. Что это?
Квадратным уравнением с переменной x называется уравнение вида ax² + bx + c = 0, где a, b, c - некоторые числа, a ≠ 0.
2. Виды квадратных уравнений.
Квадратные уравнение, где все коэффициенты (a, b, c) не равны 0, называются полными.
Неполные квадратные уравнения - квадратные уравнения, в которых b или c (вместе или по отдельности) равны 0.
3. Решение неполных квадратных уравнений.
Рассмотрим 3 варианта.
b = 0. Тогда уравнение имеет вид ax² + c = 0, a ≠ 0. Это уравнение приводится к виду x² = -(c/a). Если числа a и c одного знака, то выражение -(c/a) отрицательно, и уравнение не имеет решений. Если же числа a и c разных знаков, то выражение -(c/a) положительно, и уравнение имеет 2 решения: x = ± корень из -(c/a).
c = 0. Тогда неполное квадратное уравнение имеет вид ax² + bx = 0. Вынося общий множитель x, получаем x (ax + b) = 0. Произведение равно 0, значит хотя бы один множитель равен 0. Поэтому уравнение распадается на два линейных: x = 0 и ax + b = 0, и оно имеет два решения: x = 0 или x = -b/a.
b,c = 0. В этом случае уравнение имеет вид ax² = 0. Оно имеет решение x = 0.
4. Решение полного квадратного уравнения через дискриминант.
Дискриминант (D) = b² - 4ac.
Знак дискриминанта даёт 3 случая.
D < 0. В этом случае уравнение не имеет решений.
D = 0. В этом случае x = -b/2a
D > 0. x = (-b ± корень из (b² - 4ac))/2a
5. Решение полного квадратного уравнения через сокращённый дискриминант.
Если b = 2k, то x = (-k ± корень из (k² - ac))/a. Дискриминант в этом случае равен k² - ac.
6. Теорема Виета
Теорема Виета гласит:
Если x1 и x2 - корни квадратного уравнения ax² + bx + c = 0, то
x1 + x2 = -b/a, x1 × x2 = c/a
Теорема, обратная к теореме Виета:
Если числа x1 и x2 удовлетворяют соотношениям x1 + x2 = -b/a, x1 × x2 = c/a, то эти числа являются корнями квадратного уравнения ax² + bx + c = 0.
7. Решения квадратного уравнения с параметром.
Алгоритм:
1) Представить уравнение в стандартном виде.
2) Если коэффициент при x² есть, то рассмотреть случай: параметр равен 0.
3) Определить дискриминант.
4) Найти значения параметра, при которых D больше, равен или меньше 0. Найти корни для каждого случая.
5) В ответе указать все возможные значения параметра и соответствующие им решения.
8. Итоги.
Квадратные уравнения вида ax² + bx + c = 0 имеет много способов решений: дискриминант, теорема Виета. Также квадратные уравнения могут быть с параметром.
Если вы хотите продолжения с доказательствами и новыми способами, пишите об этом в комментариях. До встречи!
Показать полностью
Больше квадратных уравнений
Показать полностью
7
Решение квадратных уравнений
Просто смотри и учись.
#математика же
Если дискриминант больше 0 - есть два (действительных) корня у уравнения.
Если дискриминант равен 0 - только одно (действительное) решение.
Если дискриминант меньше - (действительных) решений нет. Живи с этим.
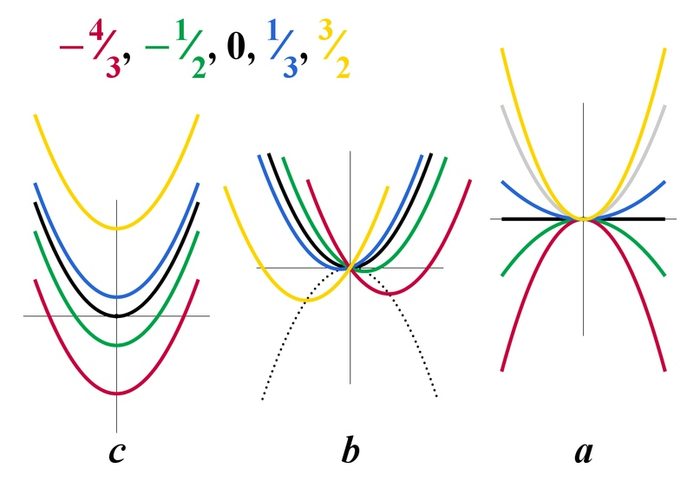
А ты любишь параболы?
Показать полностью
7
#MathMems
Мем авторский!
Часто бывало такое? 😅
Как решать квадратные уравнения?
Эту формулу все знают ещё со школы. Дискриминант равен бэ квадрат минус час (потраченного на заучивание времени). Корни находятся через дискриминант. Но что это вообще значит? Откуда взялась эта формула? Давайте разбираться
Квадратные уравнения, как и математика вообще, появились из практических задач. Их научились решать в Вавилоне ещё за 2 тысячи лет до нашей эры! Это требовалось для измерения площади земельных участков, а позже — для астрономии. Умели это делать и в Индии, ещё за 500 лет до нашей эры. Пора бы и нам понять :)
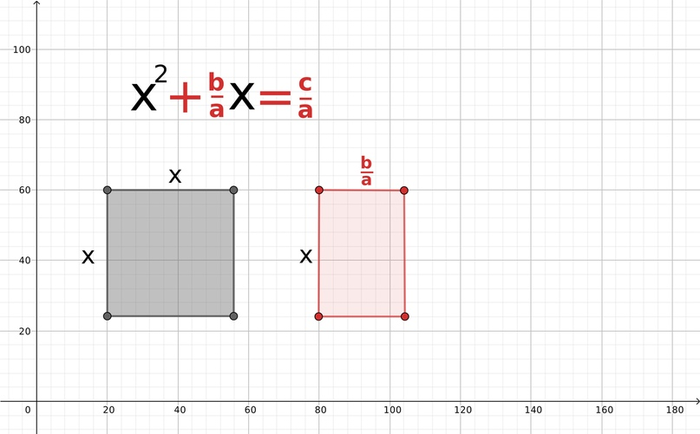
В древности задачи часто решались с помощью построений: это нагляднее и интуитивно понятнее, чем символы. Мы поступим также! Запишем такое уравнение:
Прежде чем сделать рисунок и понять, что же это такое, сделаем ещё небольшое действие: поделим всё на a, чтобы избавиться от него в начале
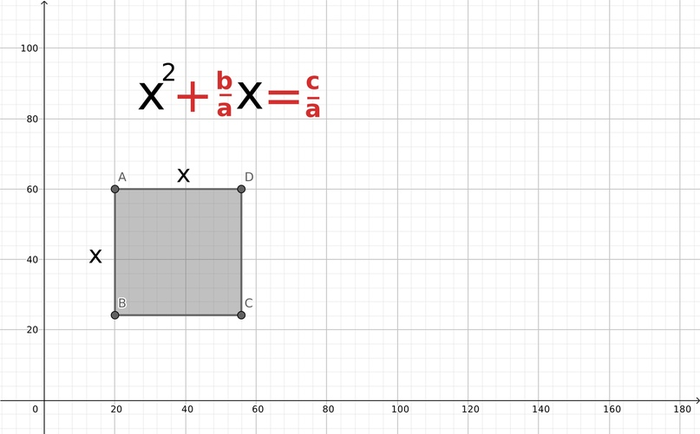
Теперь посмотрим, что же это значит. Икс в квадрате — это буквально квадрат со стороной длины x
Второе слагаемое — это прямоугольник со сторонами x и b/a
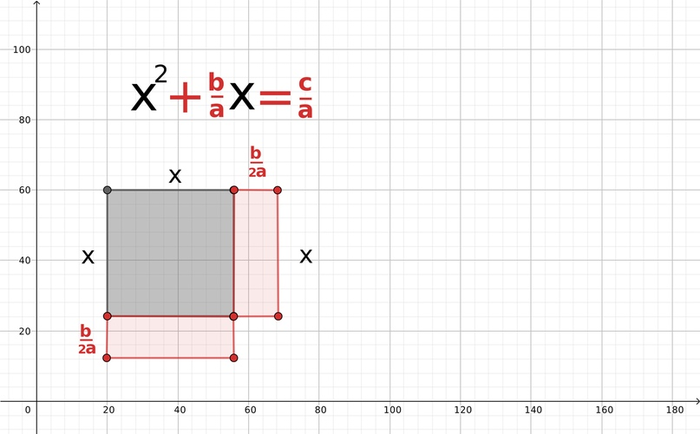
Поделим его на два прямоугольника и присоединим их к первому квадрату
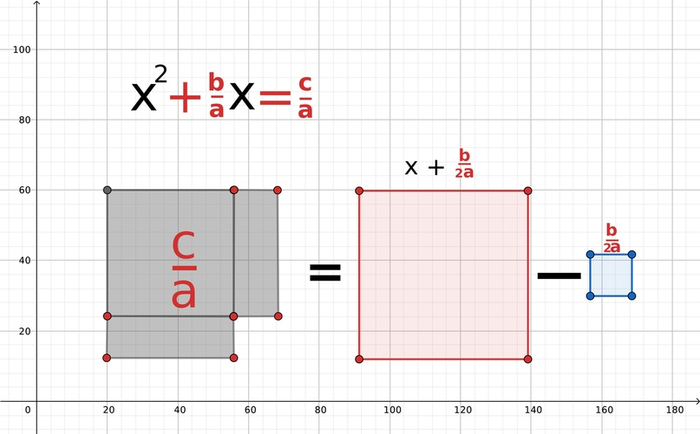
У нас почти получился ещё один квадрат! И мы знаем, что эта площадь равна c/a. Это будет равно площади большого квадрата минус площадь недостающего маленького!
Запишем всё, что мы поняли
И проделаем немного арифметики :)
Ещё несколько простых действий и мы получаем очень знакомую формулу!
Если изначально привести уравнение к стандартному виду (перенести c влево) и извлекать также отрицательный корень, получим школьную формулу
В которой, как видите, нет ничего сложного :) Пишите в комментариях, нравится ли вам такой формат постов! А также вещи, которые вы не понимаете, но хотели бы услышать простое объяснение. А если интересны ещё посты про науку и учёбу, заглядывайте ко мне в группу ВК
Показать полностью
13