Автомат с магазинной памятью (стог-памятью) и КС-языки
Предыдущая статья: Ещё раз об однозначности грамматики, о дереве вывода, а так же о главном признаке КС-грамматики в vk.com
Статья для повторения:Задача разбора, для чего она нужна? Или что такое parsing? в vk.com
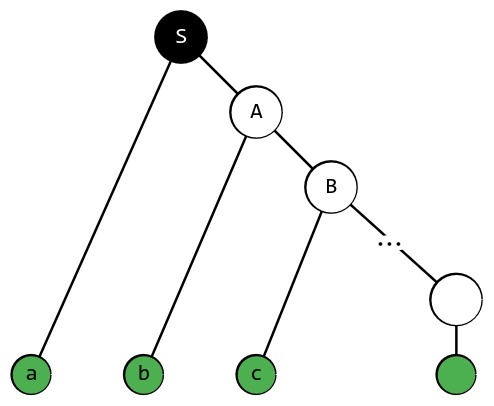
Вспомним о характере разбора цепочки. Стоит ли кость на своём месте при её постановке? Если постоянно да, то наш алгоритм предопределённый, в противном случае нам следует делать возвраты и пробовать подставить иную кость. Возможно узнать принадлежность цепочки заданной длинны, хотя бы из тех соображений, что можно построить все предложения (сентенции) грамматики совпадающие по длине с этой цепочкой.
Такой алгоритм работает по принципу полного перебора, для организации перебора используют стэк (англ. stack - рус. стог) - структуру данных по принципу «последним вошёл, первым ушёл». Полный перебор крайне неэффективен и на практике, как правило, не применяется.
Но! Есть широкий подкласс КС-грамматик, для которых накладывается ряд ограничений, что позволяет нам обходится без полного перебора и использовать эффективные алгоритмы распознавания, которые мы будем рассматривать в следующих уроках.
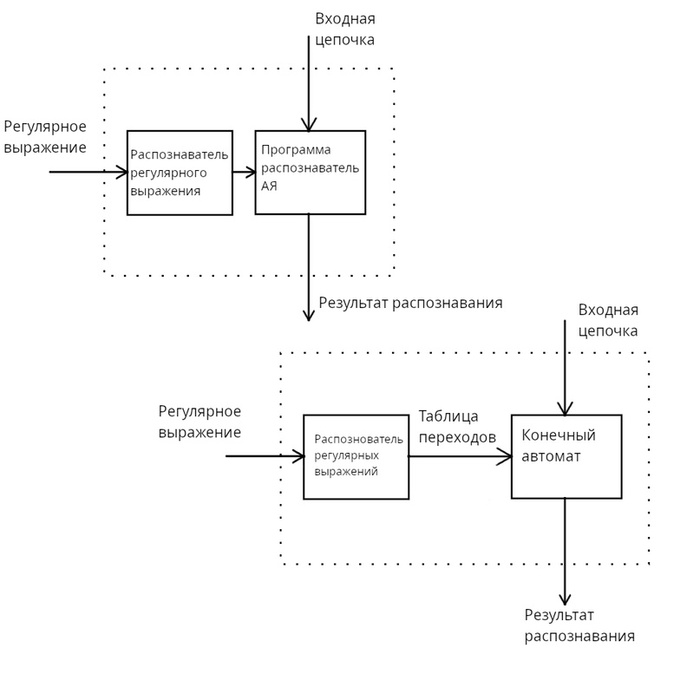
Если для автоматных грамматик в качестве распознавателя используется конечный автомат, то для КС-грамматик используется автомат с магазинной памятью.
Здесь нужно остановится на понятии «магазинная память», которое использовано крайне не удачно. По идее у вас должна быть выстроена ассоциация с магазином АК-47 (или другого оружия), где пуля заряженная последней, выстреливается первой. Но дело в том, что само слово магазин обозначает просто склад и он не обязательно должен выстроен по вышеуказанному принципу, лично я вовсе подумал о продуктовом. Поэтому используем термин стог-память или просто стог, так как если из стога вытащить что-то не сверху он превратится в кучу.
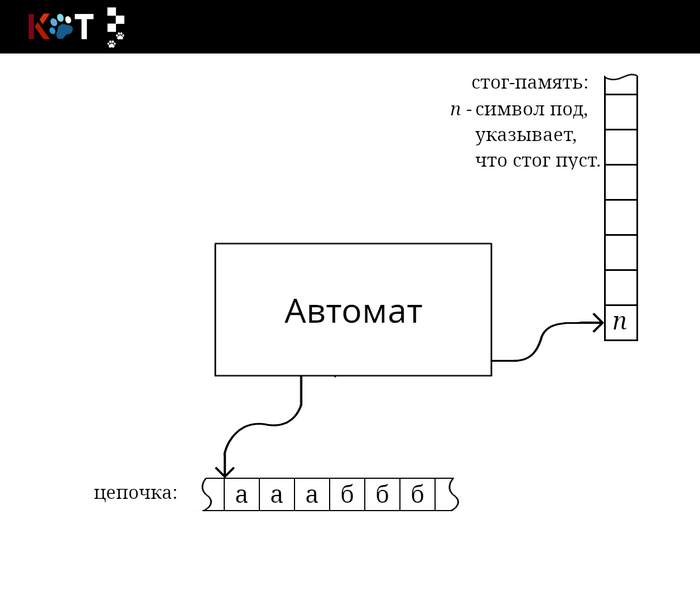
Перед тем как дать формальное описание, мы сперва построим простой стог-автомат. Отобразим общее представление об автомате:
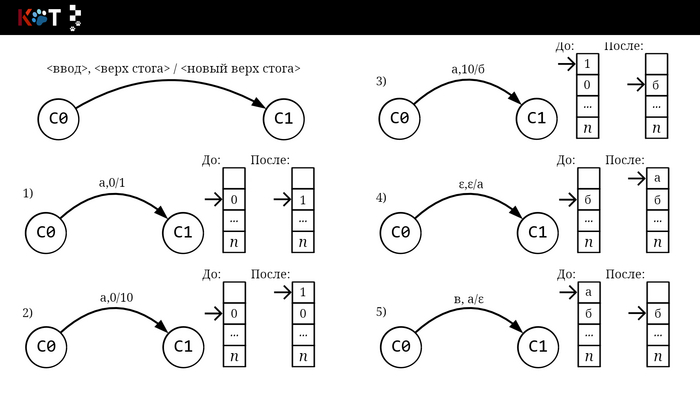
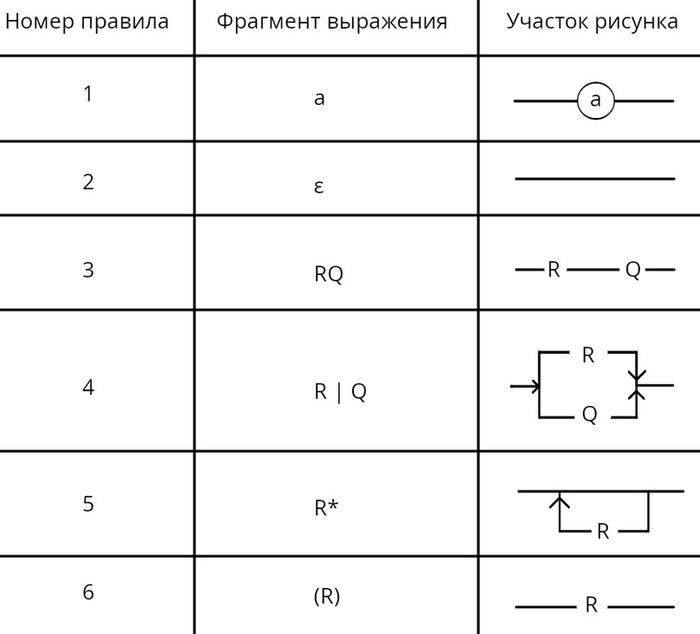
Мы видим, что автомат обращается за чтением цепочки и за чтением из стог-памяти, в стог вложен отдельный символом п обозначающий под или дно. Внутреннее устройство автомата можно представить в виде направленного графа как и конечный автомат (далее КА), только для перехода из состояния в новое состояние направленное ребро помечается по мимо принимающего символа, верхней цепочкой символов стога, которая будет заменена на новую цепочку символов в обратном порядке по очереди («первым вошёл, первым ушёл»), также входит в метку:
Выше приведены примеры переходов с отображением операций над стогом. Первых три примера прозрачны, считали символ и поменяли цепочки. В 4 и 5 используется пустая цепочка ε и здесь нужно пояснение. Между любыми двумя символами всегда лежит пустая цепочка , что является причинной почему КА с ε-переходами недетерминирован. Проверьте, зайдите https://regex101.com/, введите любой текст и регуляр (), вы получите кучу совпадений. В стог-автомате ε используется в целях внутренней работы без считывания символа принимаемой цепочки, выталкивания и помещения символов из/в стог(-а), ведь пустота означает, что нечего брать или класть.
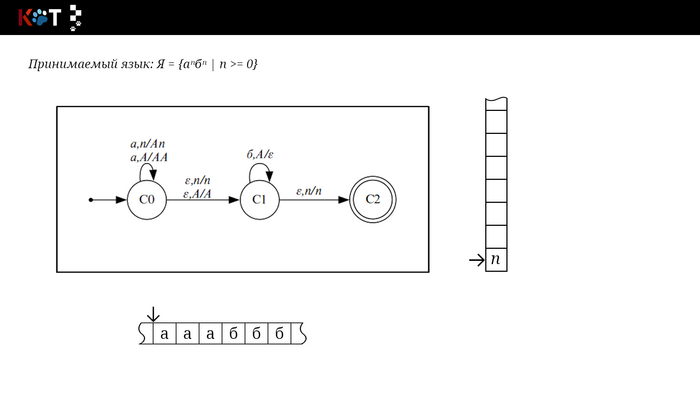
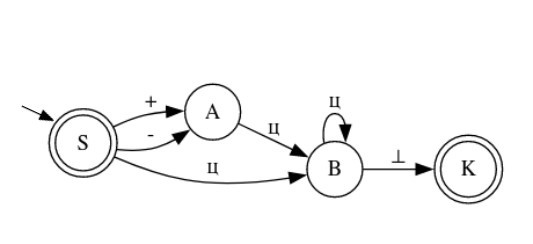
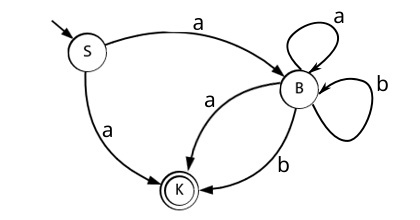
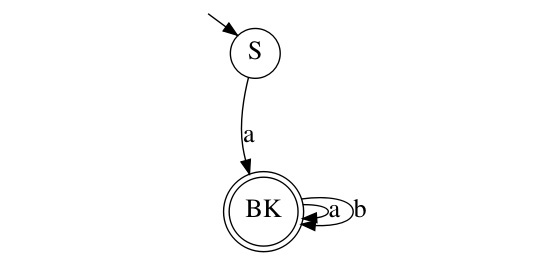
Изобразим граф стог-автомата принимающего язык:
Я = {аⁿбⁿ | n >= 0}, где в цепочках символы а и б повторяются в равном количестве, примеры { аб, аабб, аааббб, …}.
Так же как в КА конечное состояние автомата обозначаем узлом с двойным кружком, а начальное просто стрелкой. Для того, чтобы не изображать лишних рёбер правила переходов записывают друг над другом. Формально данный стог-автомат записывается так:
М = ({С0, С1, С2},{а,б}, {А. п}, δ, С0, п, {C2})
Теперь мы готовы к общему формальному описанию, приступим:
M = {Q, Σ, Γ, δ, q0, Ζ, F}
F - множество конечных (принимающих) состояний автомата, наше {C2}.
Ζ - символ конца стога, наш п - символ под.
q0 - начальное состояние автомата, наше С0.
δ - функция переходов автомата δ: ( Q × (Σ ∪ {ε}) × Γ) → (Q × Γ*).
Γ - алфавит стога, наше {А, п}.
Σ - входной алфавит, наше {а,б}.
Q - множество состояний автомата, наше {С0, С1, С2}.
Остановимся на функции переходов δ: ( Q × (Σ ∪ {ε}) × Γ) → (Q × Γ*), она нам говорит о том, что переход зависит от текущего состояния Q, от принимаемого символа Σ с возможностью его оставить в покое ε и от верха стога Γ, в замен мы получаем новое состояние Q и новое содержимое стога Γ*. Γ* - звездочка обозначает, что наше множество разрастаемое, то есть стог заполняется символами.
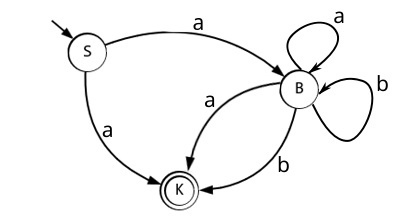
Для дальнейшего объяснения предоставляю работу автомата того же языка, но построенный по его грамматике:
G: S → aSб | ε
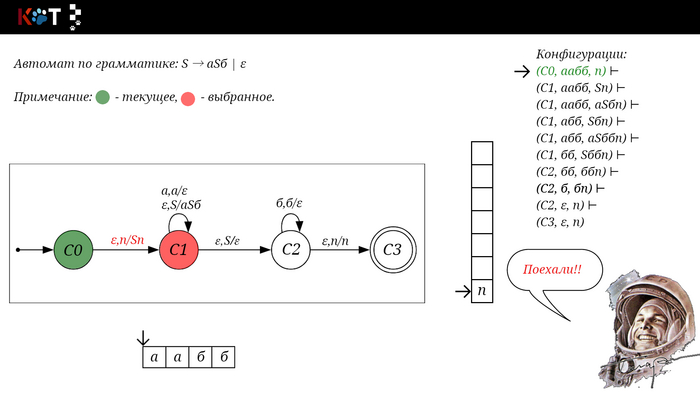
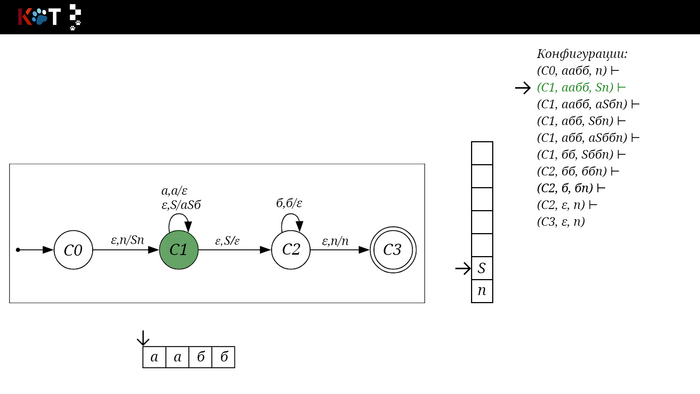
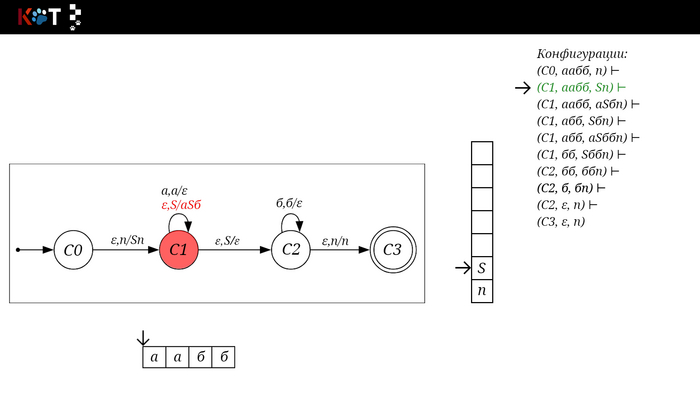
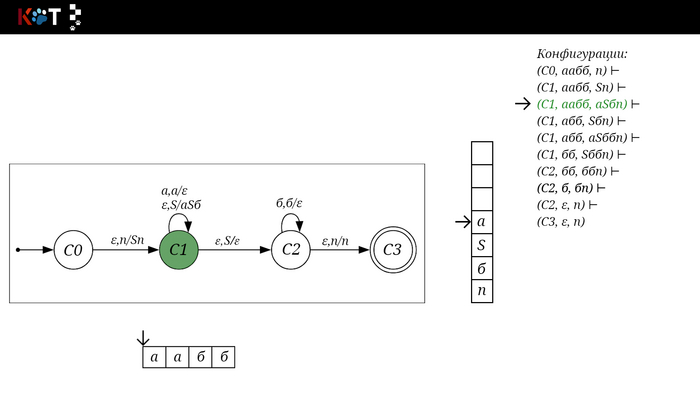
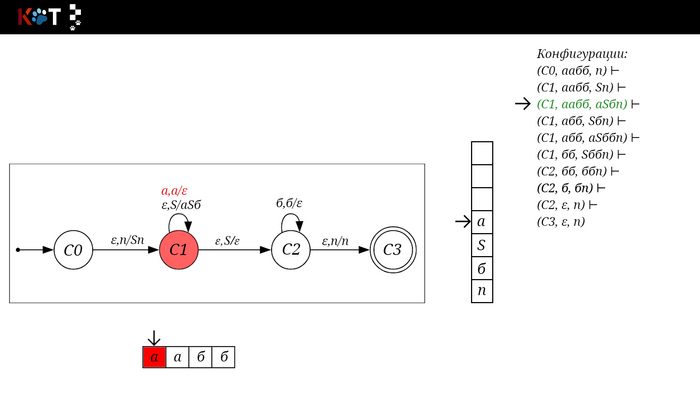
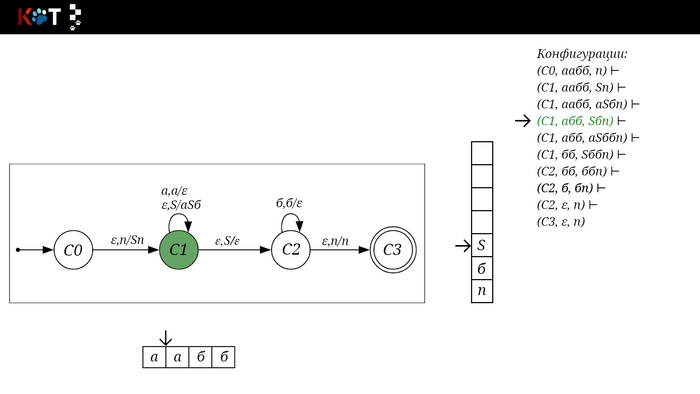
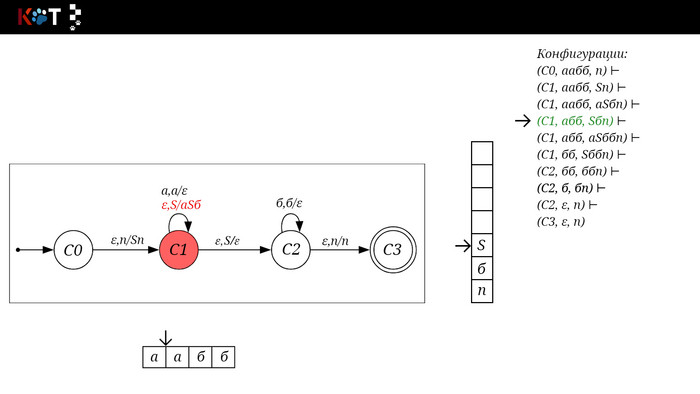
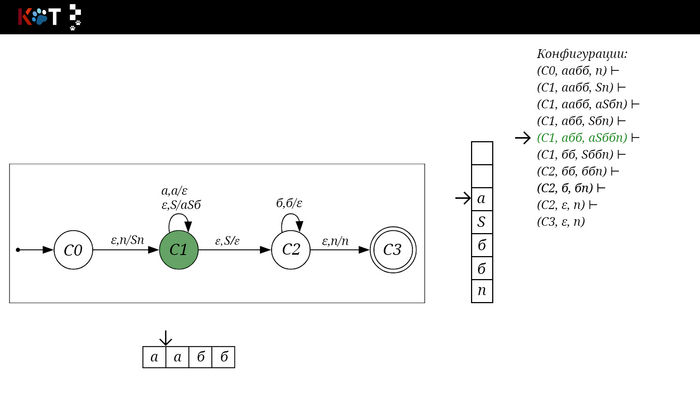
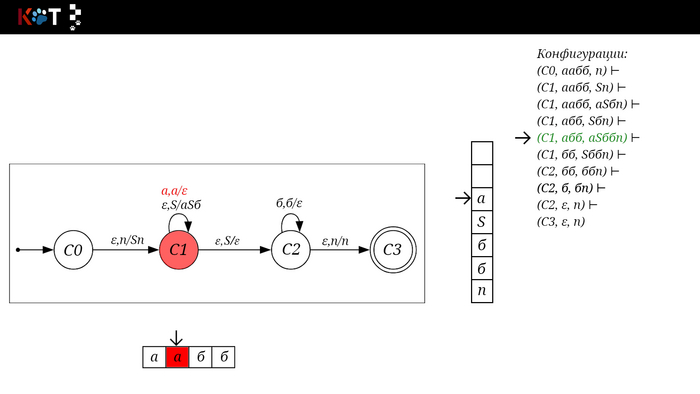
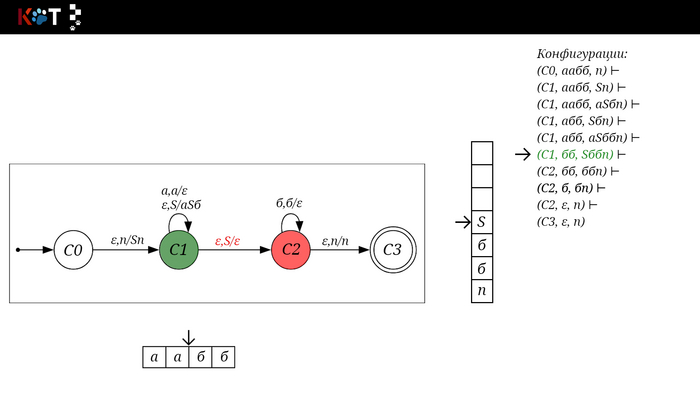
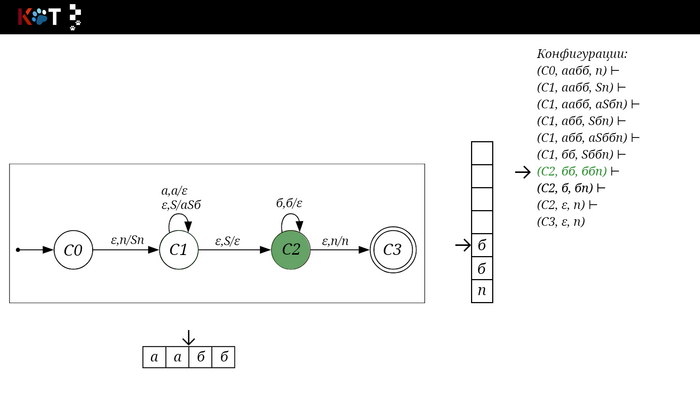
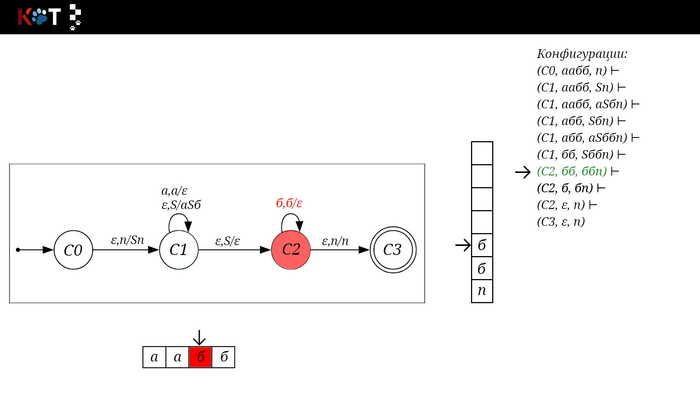
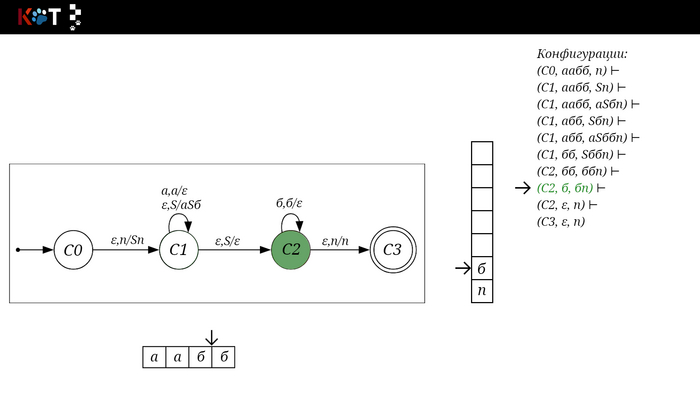
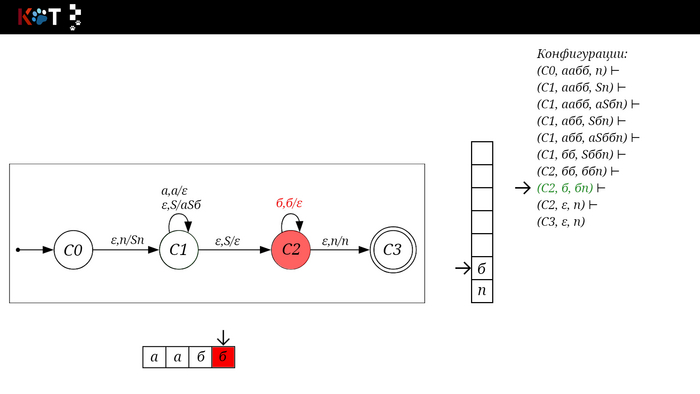
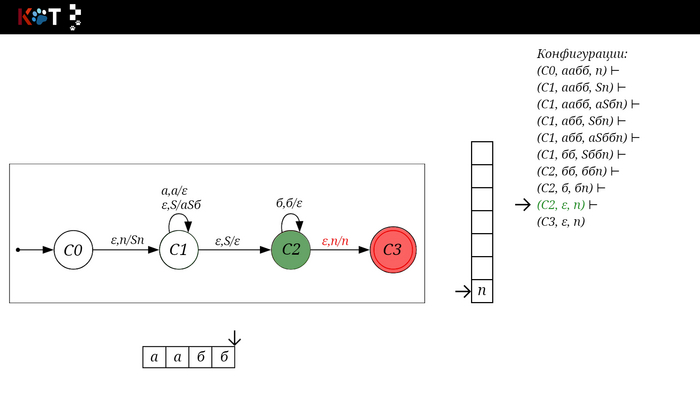
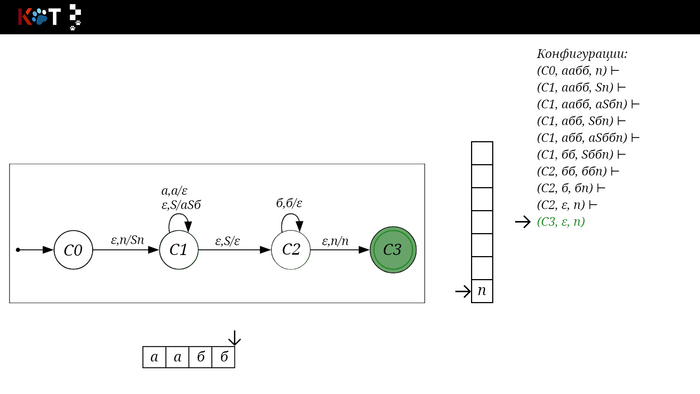
Поехали!! Листай!
На рисунке отображено, ещё не рассмотренное нами понятие конфигурации. Конфигурация представляет из себя набор (q, ω, γ), где q - текущее состояние, ω - цепочка ещё не рассмотренных символов, γ - содержимое стога. Символом ⊢ обозначают такт автомата, то есть переход из одной конфигурации в другую. Обозначим символом ⊢* последовательность ноль и более тактов, теперь мы можем описать условие принятия цепочки или допускаемый язык автомата:
L(M) = {ω ∈ Σ* и (q0, ω, Z) ⊢* (q, ε, Z), где q ∈ F} - то, есть когда наш стог опустошился до пода, завершился в конечном состоянии, а так же вся входная цепочка прочитана полностью. Лично у меня остался вопрос, почему везде записывают принятие по пустому стогу так:
L(M) = {ω ∈ Σ* и (q0, ω, Z) ⊢* (q, ε, ε,) где q ∈ F} - ведь никто не извлекает Z?
Так же существует соглашение условия принятия:
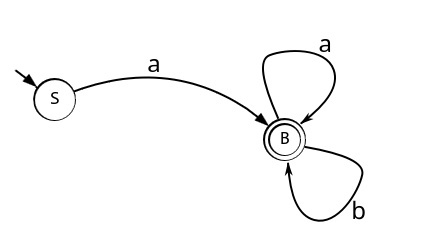
L(M) = {ω ∈ Σ* и (q0, ω, Z) ⊢* (q, ε, γ), где q ∈ F, γ ∈ Γ*} - то, есть когда наша цепочка полностью прочитана и мы достигли конечного состояния, а в стоге остались символы. Если мы уберём состояние С3, а С2 сделаем конечным, то становится понятно почему, такое соглашение есть.
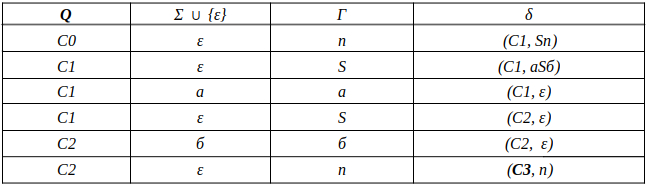
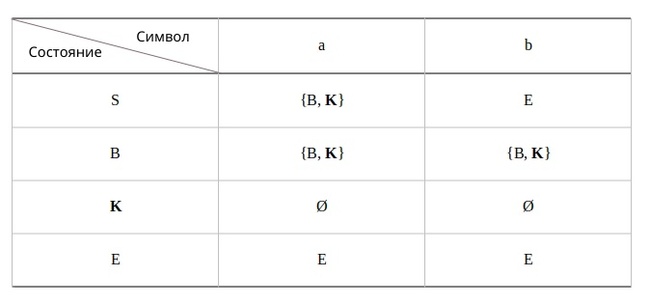
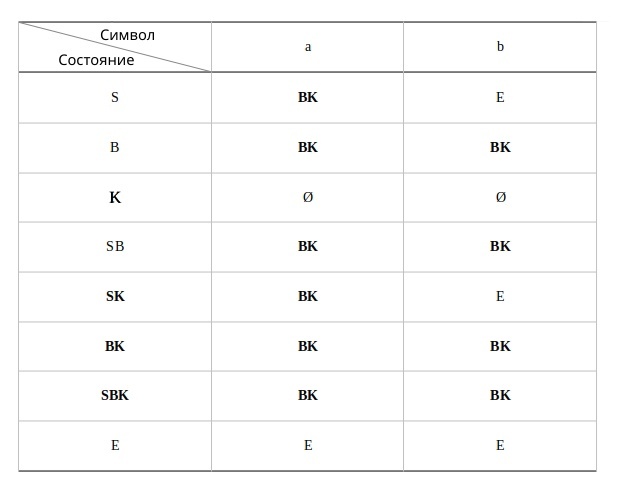
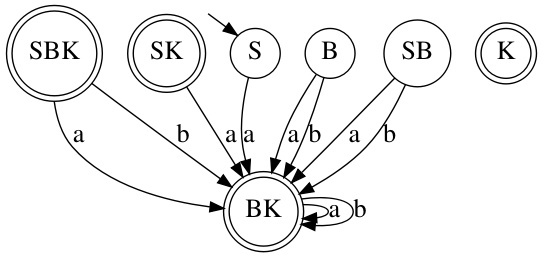
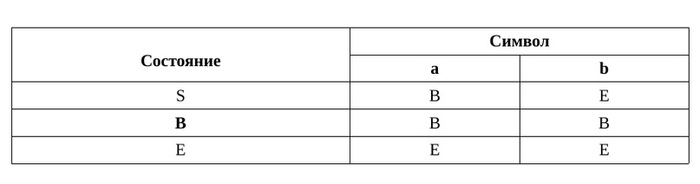
Так же автомат можно описать таблицей, вот наш случай:
В заключении следует сказать:
Для произвольной КС-грамматики можно построить недетерминированный автомат с магазинной памятью (стог-памятью), принимающий язык, порождаемый этой грамматикой.
Возможно построить и детерминированный, как отмечалось раньше, для этого грамматикам накладываются некоторые ограничения, о которых будет рассказано в других уроках.
Постскриптум: Очень сильно надеюсь, что изложил тему доступным языком. Будьте мне здоровы, подписывайтесь.