Первый пост, ругайте, но не сильно.
Недавно натолкнулся на пост и захотелось немного раскрыть тему образования, особенно в плане применимости математики в жизни. Я не являюсь профессиональным математиком или студентом мехмата, базовое образование экономическое. Но по работе имею дело со статистикой, которую, во многом, пришлось изучать самостоятельно, хотя некоторый базис был дан в универе. По этой причине, думаю, могу объяснить тему математики с немного другой стороны, нежели выпуcкники мехмата.
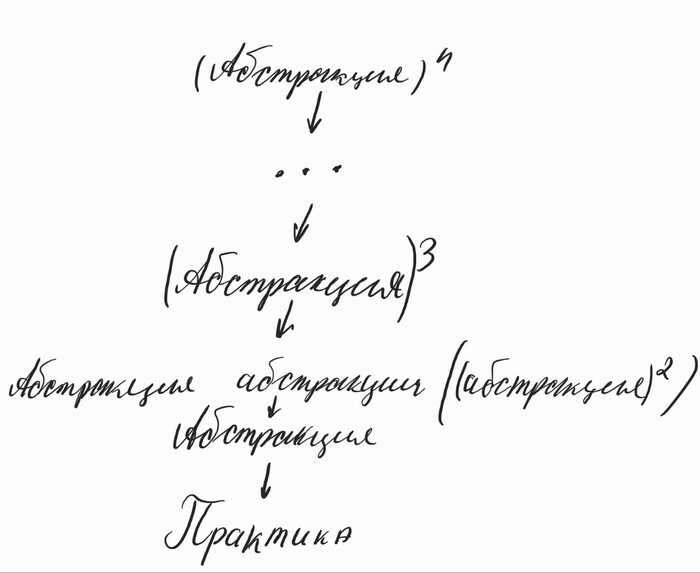
Для начала хочу раскрыть, как мне кажется, самую главную мысль. Основное в математике - это не формулы, теоремы или переменные. Все ранее названое - это лишь следствия, способы отобразить основное. А основное в этой интересной науке - это абстракция.
Большая проблема, отчего математику многие не понимают, в том, что абстракции бывают нескольких уровней и, абстракция нижнего уровня - это частное абстракции более высокого уровня. Чем выше абстракция, тем сложнее показать практический пример ее использования. Не только потому что она более оторвана от практической реальности, но и потому что она используется, чтобы свести решение задачи к абстракции нижнего уровня. И так поэтапно переходя от высоких абстракций к низким решаются практические задачи. То есть, напрямую сложные в понимании вещи не могут быть сопровождены практическим примером только опосредовано.
Приведу практический пример. Любая уважающая себя компания должна заниматься прогнозированием (обоснование данного тезиса дать могу, но сейчас не об этом). Есть много способов решения задачи прогнозирования: от расчета скользящей средней до построения нейронных сетей. Мы рассмотрим базовый эконометрический способ решения данной задачи - линейную регрессию на базе МНК (метод наименьших квадратов) и разного рода абстракции на ее примере.
Допустим, у нас есть продажи, которые постоянно увеличиваются (нам очень везет), и мы хотим понимать, как они будут увеличиваться дальше. Хитрые и умные математики подумали и решили, что можно найти такую кривую (в нашем случае линию), которая была бы ближе всего к имеющимся точкам и которая бы строилась на базе какого-то известного влияющего фактора.
Если линия близко расположена к точкам, значит она хорошо описывает природу изменений (в нашем случае, продаж). Другими словами, если мы говорим, что через месяц продажи станут равны Y, потому что X будет такой-то, и, если наш прогноз оказался самым близким к истине, то мы хорошие аналитики, понимающие природу продаж. А если мы так точно прогнозируем постоянно или даже не обязательно прогнозируем, но и объясняем случившиеся продажи также точно, то мы вообще супер-аналитики. Такая тут логика.
Начнем декомпозицию задачи по нахождению такой линии:
1) Мы, для простоты, посчитали, что линия нам подойдет, осталось понять, как эту самую линию построить. Сама по себе линия задается функцией: y = k*x + b, x- это какой-то известный нам показатель, который будет изменяться, k - это постоянное неизменяемое значение, задающее наклон линии, b - это тоже постоянное неизменное число, задающее значение y в точке, где x =0. На этом этапе нужно знать такие абстракции как функция, переменная, числа и сложение.
2) Линия должна быть близка к нашим точкам. Значит мы должны придумать функцию, которая бы рассчитывала сумму расстояний от нашей, пока еще неизвестной линии, до всех известных точек. Здесь нам очень пригодится понимание того, что переменная, задающая значение функции, тоже может быть функцией. То есть, что мы можем придумать функцию от функции, а не только от какой-то переменой и постоянных значений. Учитывая, что наша линия может отклоняться и вверх, и вниз от точки, то, чтобы положительные и отрицательные отклонения не погасили друг друга, нам необходимо лишить наши отклонения знака отрицательного числа, а значит быть знакомыми с концепциями модуля числа, степеней. Так как мы считаем сумму отклонений всех точек от линии, то надо понимать, что такое сумма и каковы ее свойства.
3) Мы придумали функцию отклонений всех известных точек от линии, которая задается параметрами искомой линейной функции (k и b). Теперь надо как-то минимизировать значение этой функции с помощью подбора этих параметров. Для этой задачи используются производные. Для каждого параметра мы посчитаем частные производные. Но так как нашей задачей является не найти отдельные несвязные значения параметров, а найти их комбинацию, работающую в рамках одной функции, то мы будем решать систему уравнений.
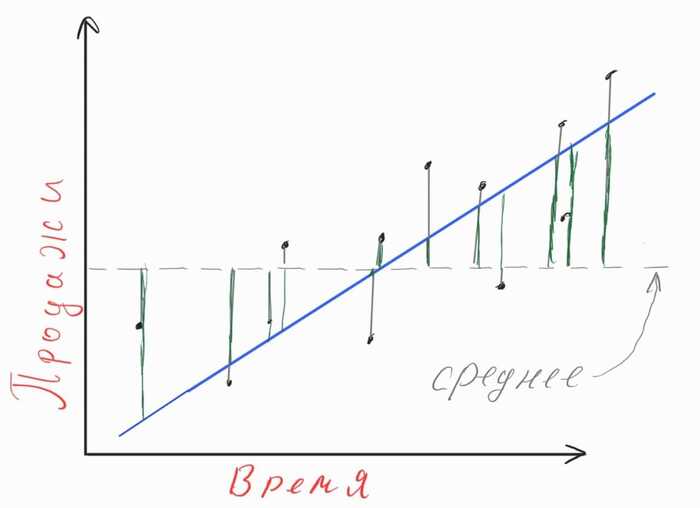
4) Мы нашли искомые параметры функции - полдела сделано. Теперь нам надо подставить значения х в найденное уравнение линии и как-то оценить, хорошо ли справляется найденная нами линия с задачей прогнозирования или объяснения зависимости продаж от времени. Методов такой оценки существует вагон и маленькая телега. Мы воспользуемся самым простым: посчитаем сумму отклонений значений найденной линии от среднего значения фактических продаж и сравним ее с суммой отклонений фактических продаж от того же среднего.
На диаграмме это отношение длин зеленых линий к длинам серых. То есть сумму длин зеленых мы поделим на сумму длин серых. Здесь мы учтем, что длина - это всегда положительное число, и, поэтому мы возведем в квадрат каждое значение отклонений и просуммируем, таким образом, избавимся от знаков "минус" в отрицательных значениях отклонений. Проведя такие манипуляции, мы получим некое усредненное значение доли отклонений, которые мы бы избежали, если бы использовали найденную линию. То есть, если увидим значение в 70%, это значит, что наша линия позволяет ошибаться на 70% меньше, чем если бы мы прогнозировали, просто рассчитав среднее от продаж. Здесь мы должны быть знакомы с концепцией дроби, процентов. График рисовался "на глазок", поэтому тут чисто визуально результат "так себе".
Подведем итог:
1) мы решили спрогнозировать продажи - практическая задача
2) мы подумали, что можем прогнозировать с помощью линии - мы должны понимать, что такое сложение, переменная, функция.
3) для того, чтобы найти линию и воспользоваться абстракциями, применяемыми во этапе 2, мы должны найти параметры функции. Для этого необходимо воспользоваться возведением в степень, производными, системами уравнений
4) мы хотим проверить, насколько хорошо мы решили задачу. Для этого необходимо понимать, что такое процент, дроби и, опять же, степень числа.
5) есть определенные статистические концепции, которые в принципе потребуются для понимания регрессии и решения задачи прогнозирования в частности: отклонения, математическое ожидание, случайная величина. Эти концепции вырастают из понимания более простых вещей, которые объясняются в школе. В этом примере для механического нахождения параметров нашей линии они не нужны, но были бы нужны, если бы мы объясняли кому-то результаты или саму тему регрессии.
Этим примером я хотел показать как такие абстрактные понятия как "система уравнений", "производные", "функции" и др. находят применение в реальной жизни. Я постарался проиллюстрировать, как при решении практической задачи нам приходится повышать уровень математической грамотности, постепенно ставя перед собой все более сложные математические задачи (подставить значения в функцию легко, куда сложнее найти эту функцию)
Простая линейная регрессия - это базовый элемент эконометрики (или машинного обучения, если хотите). А есть концепции, где полное понимание линейной регрессии - это лишь один из множества кирпичиков. Но именно из понимания множества абстрактных концепций (которые тоже строятся на абстрактных концепциях) рождаются действительно ошеломляющие инструменты: автопилот в тесле, слежение за объектом в дроне от DJI, дипфейки, распознавание объектов в роботах-пылесосах (чтобы не наехать на результаты жизнедеятельности питомца), автоматические торговые системы на биржах, средства оптимизации формы изделий на производстве.
Фото взято из поста пикабушника @iProcione
В плане новых знаний в математике, которые кажутся не нужными, я считаю правильным думать, что скорее всего они потребуются как промежуточный инструмент в какой-то большой задаче. А не думать, что если не видно практического применения сейчас, то знание и не нужно