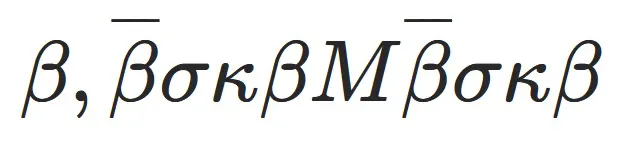Bozon.Higgs

Вопрос, конечно, интересный учитывая, что Архимед жил задолго до изобретения числа 0. С другой стороны, мы хорошо знаем какой колоссальный вклад внес этот человек в развитие наук в те давние времена. Но если он не знал цифру 0, то как он мог складывать и вычитать числа и решать сложные математические уравнения?

Все дело в системе счисления. Архимед, как и другие древние математики, не применял цифры для написания чисел так, как это мы делаем сейчас. Он не использовал позиционную нотацию для чисел и не использовал десятичные дроби. Ему, к примеру, для написания числа  «503» не надо писать 5+0+3, он записал бы это так – ΘΓ, где Θ – означает 500 и Γ – означает 3.

Эта система была характерна и для римских ученых, которые, собственно, содрали ее у греков. Только число «503» римскими цифрами выглядит как – LIII, где L означает – 500 и III означает – 3. Как видим цифры 0 нигде нет (число есть, а нуля нет).

Самая ранняя запись о цифре 0 в Греции сделана только через 100 лет после смерти Архимеда и использовалась в качестве заполнителя в таблицах, где небольшие значения были указаны в виде шестизначных дробей.

Однако Архимед экспериментировал с системами счисления, причем зашел так далеко, что изобрел метод описания и записи больших чисел, которую Википедия описывает как «напоминающую» позиционную систему. Она, описанная в книге «Песочный счетчик», рассказывает о записи чисел, сгруппированных в октеты, по 8 символов, каждый из которых представляет значения до десяти тысяч. Например, число 222 222 222 Архимед записал бы так:

Где M означает, что предшествующее значение выражено в «мириадах», или единицах 10 000, а верхняя строка означает, что число должно быть умножено на 1000. Сами цифры являются β =2, σ =200, κ =20.

Принятие нуля в качестве числа (как и принятие отрицательных чисел) заняло удивительно много времени. Но пока его не было Архимеду приходилось как-то выкручиваться. И мы видим, что с этим он справлялся и довольно неплохо, учитывая сколько открытий он сделал и сколько расчетов произвел.

Оригинал статьи - https://bozon-higgs.ru/znal-li-arkhimed-o-chisle-nol/

Немного истории

Системы счисления были придуманы давным-давно, для описания окружающей реальности, для измерения физических свойств — длина, ширина, вес, объем и так далее. С течением времени эти системы  совершенствовались, развивались, какие-то уходили в прошлое, какие-то появлялись новые.

Считать люди начали с доисторических времен. Сперва используя пальцы рук, затем пошли палки и камни. Древние пастухи, например, выкладывали две кучи камней, и перекладывали камень из одной кучи в другую каждый раз, когда овца уходила или возвращалась в стадо.

Что касается кто и когда «изобрел» цифры не знает никто. Разные группы людей имели разные системы нумерации, причем наиболее популярной была десятеричная система. Некоторые индейские племена использовали двадцатиричную систему счисления (по количеству пальцев рук и ног). Вавилоняне использовали 60-тиричную систему, больше похожую на гибридную десятеричную систему. Мы до сих пор ее используем измеряя промежутки времени и углы в геометрии (час – 60 минут, угол – 90-180 градусов и т.д.).

Теперь к сути

Арабские цифры, от 0 до 9, составляют основу современной математики. Несмотря на свое название, арабские цифры произошли вовсе не от арабов, а от древних индийцев. Те широко использовали в своей практике цифры и они, со временем, перекочевали к арабам, а уж потом попали в Европу.

Ранняя история

Девять цифр, используемых сегодня, произошли от цифр Брахми, местной индийской системы счисления III века до н. э. Буддийские надписи того времени показывают использование символов, соответствующих числам один, четыре и шесть.

В девятом веке нашей эры в академических надписях появилась цифра ноль. Однако археологические свидетельства, найденные в центральной Индии и Иране, указывают на использование всех девяти цифр еще в седьмом веке нашей эры.

Более широкое принятие

Между 825 и 830 годами персидский математик Аль-Хорезми и арабский математик Аль-Кинди написали отдельные книги о принципах использования арабских цифр.

Эти книги привели к распространению чисел на Ближнем Востоке и в некоторых частях Западной Европы. В 10 веке ближневосточные ученые использовали цифры для построения дробей и процентов. Позже в том же столетии математик по имени Синд ибн Али ввел десятичную точку. Вместе с этим появился новый способ написания чисел, называемый «песочным столом». В конце концов цифры из песочной таблицы приняли форму письменных чисел, используемых сегодня.

Европейская экспансия

Первое упоминание арабских чисел на Западе встречается в «Кодексе бдительности», историческом отчете об Испании, опубликованном в 976 году. Папа Сильвестр II начал распространять знания об арабских цифрах по всей Европе начиная с 980-х годов. Будучи студентом, будущий папа изучал одну из форм математики и просил итальянских и алжирских ученых перевести некоторые ранние математические тексты на общеевропейские языки. Более полно это было достигнуто в 1202 году с помощью книги Леонардо Пизанского под названием «Liber Abaci».

Окончательное принятие

Принятие арабских цифр в Европе было ускорено изобретением и внедрением печатного станка в 15 веке. В тот период европейцы уже всерьёз задумались о полном переходе на арабские цифры. Развитие наук и усложнение математических вычислений римскими цифрами сильно затрудняло получение результатов.

В итоге к середине 16 века арабские цифры распространились на большей части Европы, а римские, в свою очередь, остались в качестве символов для нумерации правителей, эпох, глав манускриптов и т.д.

Оригинал статьи - https://bozon-higgs.ru/kogda-i-kem-byli-pridumany-arabskie-tsifry/

Вселенная изобилует планетами. Только в нашей галактике их до 40 миллиардов, похожих на Землю. С таким количеством экзопланет многие всерьез полагают, что на некоторых неизбежно должна быть жизнь. Почему бы и нет?

Но как она может выглядеть?

Если верить Голливуду, то — на нас. Большинство научно-фантастических фильмов населяют свои миры формами жизни, очень похожими на те, что имеются у нас тут, на планете Земля. Правда, «Стражи Галактики» уводят этот подход немного в сторону, показывая Грута, гуманоида, эволюционировавшего от ботанического предка.

И все же есть фильмы с иным мнением. В фильме «Прибытие» показаны гептаподы, организмы очень непохожие ни на один вид родной земной фауны.

Чего же нам следует ожидать?

Карл Саган, побывав однажды в лагере «Прибытия», воскликнул: «инопланетяне будут сильно отличаться от нас!». И потом добавил – «Нет другого способа изучить этот вопрос, кроме как найти эту самую жизнь на другой планете».

Однако не все согласны с ними и в последние годы вопрос о том, насколько предсказуема эволюция стал предметом серьезных научных исследований.

Конвергентная эволюция — это явление при котором совершенно разные виды могут иметь относительное внешнее сходство. Обычно на это влияет адаптация видов к схожим ситуациям естественного отбора, благоприятствующему одному и тому же решению одной и той же проблемы, поставленной окружающей средой.

Мы знаем, что конвергенция — это явление распространенное и происходит вокруг нас повсюду. Взять, к примеру, дельфинов, акул и тунцов. Эти животные приобрели свою плавную форму для быстрого и эффективного передвижения в воде. Или, к примеру, молочай — растение из засушливых районов Африки — жесткое, с шипами вместо листьев, очень напоминающее кактус. Но это не кактус. Оно развило похожие на кактус черты, чтобы справиться с потерей воды и уберечься от травоядных животных.

Распространенность конвергенции привела некоторых эволюционных биологов к выводу, что эволюция предопределена, а ее результат неизбежен. Если окружающая среда неоднократно ставит одни и те же задачи, а естественный отбор неоднократно дает оптимальные решения, то эволюция должна быть повторяема. И, как следствие, мы можем предсказать, как может выглядеть жизнь на планете, подобной Земле.

Взять, к примеру, человека. Человек — это организм в высшей степени приспособленный и адаптированный к земным условиям, с явным желанием, волей и возможностью к глобальному доминированию в природе. Следовательно, если эволюция предопределена, то ожидание подобных вещей на другой планете очевидно, а гуманоидные формы должны развиваться и доминировать, так же как и мы. Выходит, Голливуд был прав?

Возможно. Но у этих аргументов есть кое-какие проблемы. Список примеров схожести, безусловно, впечатляет, но было бы неплохо составить список столь же впечатляющих непохожестей. Взять, к примеру, животных, которые эволюционировали только один раз и без близкого соответствия — слоны, киви, ленивцы и, конечно же, утконос с утиным клювом. Каждый из этих животных эволюционировал всего один раз, без какого-либо близкого эволюционного соответствия.

Если эволюция настолько предопределена, а ее результат настолько предсказуем, то как понять, что для этих животных нет совпадений? Ручьи, подобные тем, в которых обитают утконосы, встречаются на всех континентах, но живет утконос только в Австралии. Подходящие ветви тропических деревьев встречаются по всему миру, но ленивцы эволюционировали только в Южной Америке.

Вопрос больше не в том, является ли конвергенция или не является общим явлением: теперь мы знаем, что и то, и другое является общим. Скорее, ученые заинтересованы в понимании того, почему конвергенция происходит в одних случаях и не происходит в других. Это еще только начало, но вывод уже ясен: близкородственные виды (или популяции одного и того же вида), как правило, адаптируются одинаково из-за своей схожести и естественный отбор, вероятно, изменит их аналогичным образом. Напротив, отдаленно родственные виды, изначально отличающиеся по многим признакам, с гораздо большей вероятностью найдут разные способы адаптации к одной и той же ситуации. Подумайте о разнице между птицами и млекопитающими: У первых есть клювы, у вторых — зубы и когти.

При всех различиях, которые должны демонстрировать такие формы жизни, естественный отбор может создавать хорошо адаптированные, но совсем непохожие на нас виды. И киви с ленивцами говорят нам об этом. А это значит, что мнение меньшинства в Голливуде почти наверняка тоже правильное.

Оригинал статьи - https://bozon-higgs.ru/mogut-li-inoplanetyane-byt-pokhozhi-na-nas/

Это видео было записано 27 сентября 2023 года. Зонд находился на расстоянии… (вы только вдумайтесь)… 7 млн километров от поверхности Солнца! Ну разве ЭТО не круто?

Телеграмм-канал

Согласно поиску в Яндексе, диаметр Земли составляет около 12 742 км или 12 742 000 метров.

Гуголплекс, между тем, равен 10^googol (или 10^10^100) метров. Гугол, записанный на бумаге выглядит так:

10000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000

Я даже не буду это комментировать. Вы сами видите все эти нули после единицы. Но гуголплекс еще больше.

Итак, имея это в виду, давайте все же продолжим наше небольшое сравнение размеров. Земля, и это хорошо видно, даже рядом не стоит с гуголплексом.

Но что насчет Солнца? Солнце намного больше Земли, верно?

Тут тоже все, не слава Богу. Диаметр Солнца составляет примерно 1 391 000 км, или 1 391 000 000 метров.

Упс, похоже, Солнце тоже не справилось.

А как насчет Солнечной системы? Наша Солнечная система, от одного края до другого, будет... подождите... Яндекс сообщает, диаметр Солнечной системы равен 100 000 а.е., что эквивалентно 100 000 х 149 597 870 700 метров (1 а. е. в метрах) = 14 959 787 070 000 000 метров.

Это очень большое число. Но даже оно намного меньше гугола, не говоря уже о гуголплексе.

Что ж, давайте перейдем на следующий уровень.

Как насчет нашей галактики?

В конце концов, Солнечная система всего лишь крошечная точка в огромных масштабах космоса. Давайте посмотрим, как наше чудовищное число выдержит такое сравнение…

…Ладно, думаю, вы уже поняли, что будет дальше. Диаметр Млечного Пути составляет около 105 700 световых лет, или 1,0006619x10^18 км. Это очень большое число, настолько большое, что я не стал его записывать в метрах…

Но это тоже даже близко не гугол, и уж тем более не гуголплекс.

Думаю, хватит мелочиться. Давайте сразу перейдем к сути.

Диаметр всей наблюдаемой Вселенной оценивается примерно в 93 миллиарда световых лет. Это совершенно ошеломляющий размер, эквивалентный 8,8 x 10^23 км (или 8,8 x 10^26 м)… но и ЭТО намного, намного меньше одного гугола.

А гугол, как вы помните, ничтожно мал по сравнению с гуголплексом.

Да-а, размер в один гуголплекс будет явно больше, чем вся наблюдаемая Вселенная. Настолько больше, что вы даже представить себе не можете.

И это, наверняка, будет больше всего того, что существует в настоящее время.

Скажу больше, если мы гуголплекс понизим до миллиметров, он все равно будет больше всей нашей Вселенной. Жуть!!!

Когда я впервые увидел этот вопрос, я подумал, что это хорошая разминка для ума. Не надо быть астрофизиком, или космологом, чтобы попытаться сравнить все эти размеры. Достаточно иметь пытливый ум, справочную информацию, калькулятор и… много, много воображения. Без не него, увы, никуда.

Статья с моего телеграмм-канала - https://t.me/bozon_higgs_ru