Гиперкубоид, как функция времени⁠⁠

Привет, друзья!

Знаю, что вы любите картинки больше, чем скучные формулы, в которых нужно еще разбираться, а время? Где его взять? Вот-вот! Картинки лучше! Дарю:)

Преамбула. В трехмерном пространстве существуют т.н. Кирпичи Эйлера. Леонард Эйлер, живший в XVIII веке по большей части в России, был одним из величайших математиков всех времен. И о чудо! Он уделил рациональным кубоидам столько своего времени и внимания, что с тех пор их называют Кирпичи Эйлера.

На первый взгляд в Кирпичах Эйлера нет ничего сложного.  Три+три прямоугольные грани, на гранях ребра и диагонали образуют целочисленные пифагоровы тройки, однако оказалось чрезвычайно сложно отыскать закономерности, которые к этим Кирпичам приводят. Сам Эйлер открыл, как пишут, две закономерности, я смог отыскать в интернете только одну.  Она повторяет параметрическую формулу Николаса Сондерсона, ранее опубликованную в Англии.  Вообще Сондерсон - удивительная фигура, англичане ставят его в один ряд с Ньютоном.

Здесь он на гравюре под названием "Сокровища Англии" в правом нижнем углу, а вот здесь он еще подростком:

Сондерсон ослеп в совсем юном возрасте и все свои открытия совершил, будучи слепым (невероятно!). Однако этот портрет меня заинтересовал атрибутами. Написать картину в то время - недешевое удовольствие. Сондерсон сидит на фоне картины (опять таки, недешевое удовольствие), а его одеяние указывает на знатное происхождение. Думаю, от графа до герцога. Немного отвлекся...

В общем, с тех времен математики возвращаются к задаче периодически, но вместо того, чтобы для начала описать эйлеровы кирпичи исчерпывающими законами их образования, рассуждают на тему пространственной диагонали. Даже формулу Сондерсона-Эйлера толком не исследовали. В своем предыдущем посте я этот пробел исправил, а здесь предлагаю ГИФ-ки, что такое Гиперкубоид Сондерсона-Эйлера, как функция времени. Все что ниже отрисовано с достаточной точностью.

Одна проекция

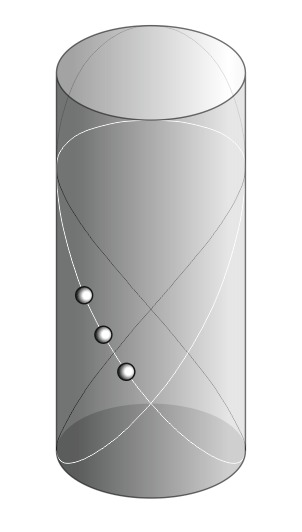
Другая проекция

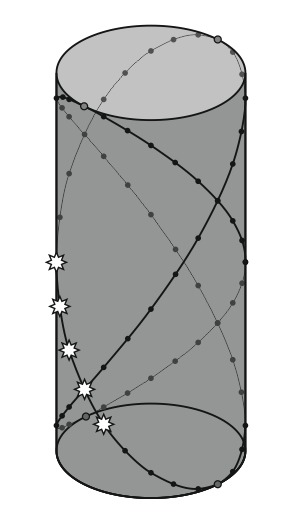
А здесь, как выглядят кубоиды, получаемые по формуле Сондерсона-Эйлера, в одной из проекций:

Кстати, в этой нижней картинке я обнаружил одно удивительное свойство для некоторых Кирпичей Эйлера. А Вы сможете? :)  Подсказка: в формуле Сондерсона-Эйлера рациональные значения ребер кирпичей получаются из двух рациональных чисел, а значит... Впрочем, пока это на уровне гипотезы.

(Игорь)