Если вы уже долгое время ездите одним и тем же маршрутом, то, вероятно, определили для себя самый лучший путь. Но понятие «лучший» весьма расплывчато. Возможно, однажды произойдет авария или перекроют дорогу, и ваш самый быстрый маршрут станет самым медленным.
Подобные ситуации представляют вызов и для исследователей, разрабатывающих алгоритмы — пошаговые процедуры, которые компьютеры используют для решения задач. Существует множество алгоритмов, способных решить любую заданную проблему, и вопрос о том, какой из них лучший, может быть крайне неоднозначным.
Например, представьте алгоритм, предназначенный для поиска самого быстрого маршрута между двумя точками. Есть множество способов спроектировать такой алгоритм, чтобы он не давал сбоев. Успешный алгоритм всегда вернет самый быстрый маршрут, независимо от того, используете ли вы его в Лондоне или Лос-Анджелесе, и независимо от того, час пик это или глубокая ночь.
Но эти алгоритмы не одинаковы. Время, которое каждый из них затрачивает на поиск правильного ответа, будет варьироваться в зависимости от того, где и когда он используется, и случаи, которые сложны для одного алгоритма, могут быть простыми для другого. Идеально было бы иметь алгоритм, который всегда работает быстрее остальных.
Для большинства задач найти такой «единорог» просто невозможно. Но новое доказательство показывает, что для классической задачи поиска пути существует алгоритм, близкий к идеалу: при самых худших сценариях трафика это лучший подход на любой возможной уличной сети. Более того, этому алгоритму почти 70 лет, и он является основой учебной программы по информатике в университетах. Новая работа будет представлена на следующей неделе на симпозиуме по основам компьютерных наук 2024 года и получит награду за лучшую статью.
«Это потрясающе», — сказал Тим Рафтгардэн, компьютерный ученый из Колумбийского университета. «Я не могу представить более убедительную научную работу о проблеме, которую мы преподаем студентам на курсе алгоритмов».
История этого знакового алгоритма поиска пути началась с обходного пути. В 1956 году 26-летний голландский компьютерный ученый Эдсгер Дейкстра хотел написать программу, которая продемонстрировала бы возможности новейшего компьютера ARMAC. Во время прогулки по магазинам со своей невестой в Амстердаме он зашел в кафе передохнуть. Именно тогда ему пришла в голову идея алгоритма, который теперь носит его имя. У него не было с собой письменных принадлежностей, поэтому в течение 20 минут он разработал все детали в уме.
В интервью незадолго до своей смерти Дейкстра приписывал непреходящую привлекательность своего алгоритма, в том числе, и его необычной истории происхождения. «Без ручки и бумаги вы почти вынуждены избегать всех лишних сложностей», — сказал он.
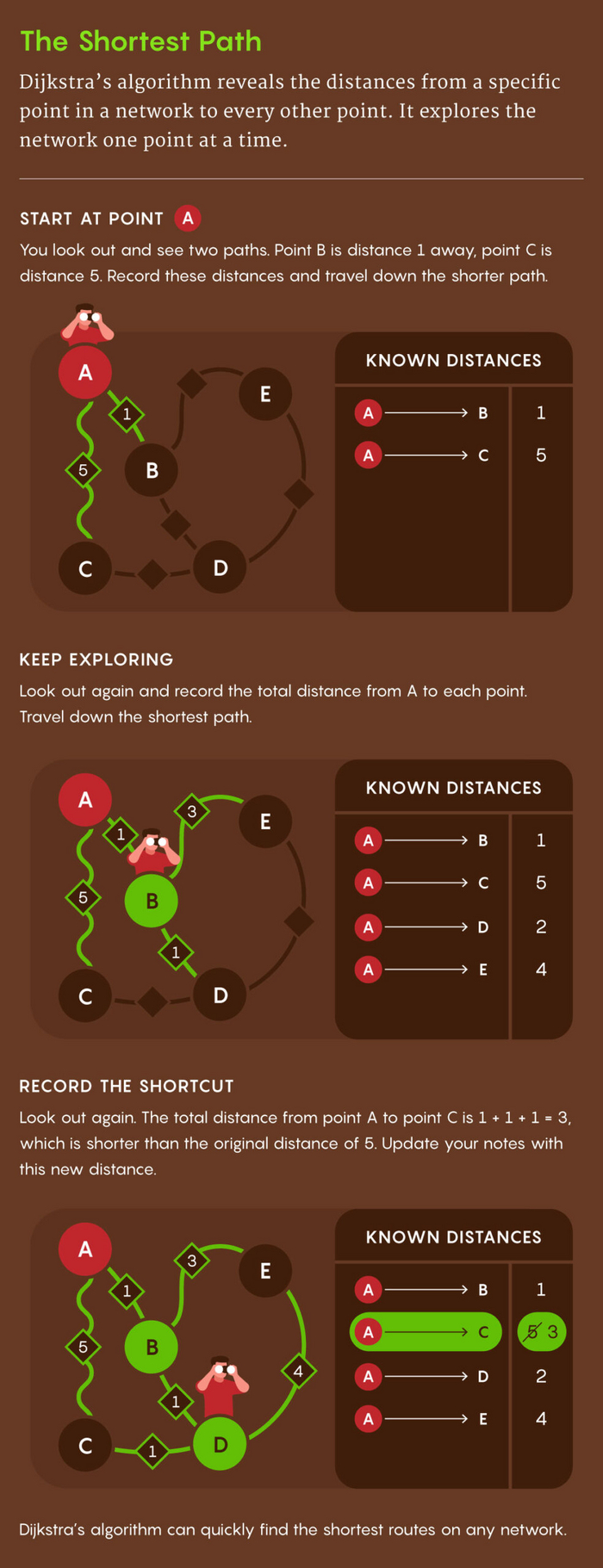
Алгоритм Дейкстры не просто сообщает вам самый быстрый путь к одному месту назначения. Вместо этого он дает упорядоченный список времени в пути от вашей текущей позиции до каждой другой точки, которую вы могли бы захотеть посетить — решение задачи о кратчайших путях из одной вершины. Алгоритм работает в абстрактной карте дорог, называемой графом: сети взаимосвязанных точек (вершин), в которой связи между вершинами помечены числами (весами). Эти веса могут представлять время, необходимое для прохождения каждой дороги в сети, и они могут меняться в зависимости от трафика. Чем больше вес, тем больше времени требуется для прохождения этого пути.
Чтобы понять алгоритм Дейкстры, представьте, что вы блуждаете по графу, записывая время в пути от вашей стартовой точки до каждой новой вершины на черновике. Когда у вас есть выбор, в каком направлении исследовать дальше, направляйтесь к ближайшей вершине, которую вы еще не посетили. Если вы обнаружите более быстрый путь к какой-либо вершине, запишите новое время и зачеркните старое. Когда вы уверены, что нашли самый быстрый путь, перенесите время в пути из заметок в отдельный, более аккуратный список.
«Это отличный алгоритм», — сказал Эрик Демейн, компьютерный ученый из Массачусетского технологического института. «Он очень быстрый, простой и легкий в реализации».
Чтобы применить эту процедуру на практике, вам нужно решить, как организовать свои заметки — структуру данных, в терминологии компьютерных наук. Это может показаться незначительной технической деталью, но время, потраченное на поиск по вашим заметкам каждый раз, когда вам нужно отредактировать или удалить запись, может существенно повлиять на общее время выполнения алгоритма.
В статье Дейкстры использовалась простая структура данных, оставляющая место для улучшения. В последующие десятилетия исследователи разработали более совершенные, ласково называемые «кучами», в которых некоторые элементы легче найти, чем другие. Они используют тот факт, что алгоритму Дейкстры нужно удалять только запись для ближайшей оставшейся вершины. «Куча — это, по сути, структура данных, которая позволяет делать это очень быстро», — сказал Вацлав Рожонь, исследователь из Института компьютерных наук, искусственного интеллекта и технологий (INSAIT) в Софии, Болгария.
В 1984 году два компьютерных ученых разработали изящный дизайн кучи, который позволил алгоритму Дейкстры достичь теоретического предела, или «нижней границы», по времени, необходимому для решения задачи о кратчайших путях из одной вершины. В определенном смысле эта версия алгоритма Дейкстры является наилучшей возможной. Это было последним словом в стандартной версии проблемы почти на 40 лет. Все изменилось, когда несколько исследователей внимательно изучили, что означает быть «лучшим».
Исследователи обычно сравнивают алгоритмы, изучая, как они ведут себя в наихудших сценариях. Представьте себе самую запутанную уличную сеть в мире, затем добавьте особенно сложные схемы трафика. Если вы настаиваете на поиске самых быстрых маршрутов в этих экстремальных условиях, версия алгоритма Дейкстры 1984 года непревзойденна.
Но, к счастью, в вашем городе нет худшей уличной сети в мире. Поэтому вы можете спросить: существует ли алгоритм, который непревзойден на любой дорожной сети? Первый шаг к ответу на этот вопрос — сделать консервативное предположение, что каждая сеть имеет наихудшие схемы трафика. Затем вы хотите, чтобы ваш алгоритм находил самые быстрые пути через любой возможный граф, предполагая наихудшие возможные веса. Исследователи называют это условие «универсальной оптимальностью». Если бы у вас был универсально оптимальный алгоритм для более простой задачи нахождения пути от одной точки графа к другой, это могло бы помочь вам избежать пробок в час пик в любом городе мира.
«Это звучит слишком хорошо, чтобы быть правдой», — сказал Бернхард Хойплер, компьютерный ученый, связанный с INSAIT и Швейцарским федеральным технологическим институтом в Цюрихе (ETH Zurich).
Хойплер был очарован идеей универсальной оптимальности, когда писал грантовое предложение в середине 2010-х годов. Многие исследователи считают эту часть работы утомительной, но Хойплер видел в этом возможность. «Это позволяет отбросить скептицизм и просто мечтать по-крупному», — сказал он.
Эти мечты воплотились в 2021 году, когда Хойплер и два его аспиранта доказали возможность построения универсально оптимальных алгоритмов для нескольких важных задач на графах. Он не задумывался о том, достижимо ли то же условие для классической задачи о кратчайших путях из одной вершины. Это должно было подождать, пока другой аспирант не осмелился мечтать по-крупному.
В начале 2023 года Вацлав Рожонь был на последнем этапе своей аспирантуры в ETH Zurich. Он только что завершил работу над статьей о выходе за рамки анализа наихудшего случая в другом контексте и размышлял над новыми идеями вместе со своим соавтором Якубом Тетеком, тогда аспирантом Копенгагенского университета. Рожонь предложил попробовать разработать универсально оптимальный алгоритм для задачи о кратчайших путях из одной вершины.
«Я сказал: "Нет, это невозможно; этого просто не может быть"», — вспоминает Тетек. Но Рожонь убедил его попробовать. Весной команда увеличилась до трех с присоединением Ричарда Гладика, аспиранта ETH Zurich, с которым Рожонь и Тетек познакомились еще в школьные годы в Чехии.
Трио экспериментировало с различными аспектами алгоритма Дейкстры и используемой им кучи, и им удалось собрать универсально оптимальный вариант. Но полученный алгоритм был сложным, и они не могли определить, какие условия действительно необходимы для универсальной оптимальности. В области, которая ценит всеобъемлющие и строгие доказательства, этого было недостаточно.
Тогда три студента решили переключиться с математических сетей на социальные. Рожонь начал обсуждать проблему с Хойплером, когда оба посещали коллег в Нью-Йорке. Оттуда Хойплер полетел в Панаму на отдых, но он не был готов оставить проблему.
«Это действительно был отпуск», — сказал он. «Но думать не перестаешь».
Во время звонка по Zoom через несколько дней после начала поездки Хойплера команда из четырех человек решила попробовать новый подход. Они решили сосредоточиться главным образом на выборе структуры данных. Вскоре они начали подозревать, что этого будет достаточно — они могут оставить остальную часть алгоритма Дейкстры без изменений. В течение месяца они это доказали.
Ключевым ингредиентом оказалась особая характеристика некоторых структур данных, которая позволяет быстро получать доступ к недавно добавленным элементам. Кучи с этим свойством были впервые созданы более 20 лет назад, но за все последующие годы никто не использовал их в полной мере. Четыре исследователя доказали, что им нужно только построить структуру данных с этим новым свойством и всеми другими функциями кучи 1984 года. Теперь им оставалось только спроектировать ее.
Последним, кто присоединился к команде, был Роберт Тарджан, компьютерный ученый из Принстонского университета, который был одним из изобретателей той самой кучи 1984 года. Тарджан получил Премию Тьюринга, считающуюся высшей наградой в области компьютерных наук, и также был наставником Хойплера в конце 2000-х годов. Когда Тарджан посетил Цюрих в мае, Хойплер пригласил его на свое фирменное фондю и упомянул о новом проекте по кратчайшим путям. Тарджан сразу же присоединился.
Пять исследователей приступили к разработке структуры данных кучи со всеми необходимыми свойствами. Они начали с громоздкого дизайна и улучшали его шаг за шагом, пока наконец не остались довольны. «Каждый раз, когда мы смотрели на это, мы могли немного упростить», — сказал Рожонь. «Я был действительно удивлен, насколько простым это оказалось в итоге».
Некоторые варианты алгоритма Дейкстры нашли практическое применение в программном обеспечении, таком как Google Maps. Новый результат, вероятно, не будет иметь таких практических приложений, для которых существует множество других факторов помимо теоретических гарантий оптимальности. Но он может изменить то, как исследователи изучают оптимальность, побуждая их выходить за рамки обычного анализа наихудшего случая. Часто алгоритмы достигают более сильных гарантий за счет дополнительной сложности. Новый результат предполагает, что простые алгоритмы с такими более сильными гарантиями могут быть более распространены, чем исследователи ранее думали — команда уже идентифицировала два других примера.
«Общая концепция очень убедительна», — сказал Тарджан. «Время покажет, насколько далеко можно зайти».